El árbol comienza con el KnotenNodo ist eine digitale Plattform, die die Verbindung zwischen Fachleuten und Unternehmen auf der Suche nach Talenten erleichtert. Durch ein intuitives System, Ermöglicht Benutzern das Erstellen von Profilen, Erfahrungen austauschen und Zugang zu Stellenangeboten erhalten. Der Fokus auf Zusammenarbeit und Networking macht Nodo zu einem wertvollen Werkzeug für diejenigen, die ihr berufliches Netzwerk erweitern und Projekte finden möchten, die mit ihren Fähigkeiten und Zielen übereinstimmen.... raíz que consta de los datos completos y, anschließend, Verwenden Sie intelligente Strategien, um Knoten in mehrere Zweige zu unterteilen.
Der ursprüngliche Datensatz wurde dabei in Teilmengen unterteilt.
Um die grundlegende Frage zu beantworten, dein unbewusstes Gehirn macht einige Berechnungen (im Lichte der unten aufgezeichneten Beispielfragen) und kauft am Ende die nötige Menge Milch. Ist das normal oder unter der Woche?
An Werktagen benötigen wir 1 Liter Milch.
Es ist ein Wochenende? Am Wochenende brauchen wir 1,5 Liter Milch.
Ist es richtig zu sagen, dass wir heute auf Gäste rechnen?? Wir müssen kaufen 250 Zusätzliche ML Milch für jeden Gast, usw.
Bevor Sie zur hypothetischen Idee von Entscheidungsbäumen springen, Wie wäre es, wenn wir zunächst erklären, was Entscheidungsbäume sind?? es ist mehr, Warum wäre es eine gute Idee für uns, sie zu verwenden??
Warum Entscheidungsbäume verwenden??
Entre otros métodos de überwachtes LernenÜberwachtes Lernen ist ein Ansatz des maschinellen Lernens, bei dem ein Modell mit einem Satz von beschrifteten Daten trainiert wird. Jede Eingabe im Dataset ist mit einer bekannten Ausgabe verknüpft, So kann das Modell lernen, Ergebnisse für neue Eingaben vorherzusagen. Diese Methode wird häufig in Anwendungen wie der Bildklassifizierung eingesetzt., Spracherkennung und Trendvorhersage, und unterstreicht seine Bedeutung in..., baumbasierte Algorithmen Excel. Dies sind Vorhersagemodelle mit höherer Präzision und einfacherem Verständnis.
Wie funktioniert der Entscheidungsbaum?
Es gibt verschiedene Algorithmen, die geschrieben wurden, um einen Entscheidungsbaum zu erstellen, die für das Problem verwendet werden können.
Einige der am häufigsten verwendeten Algorithmen sind unten aufgeführt:
• WAGEN
• ID3
• C4,5
• CHAID
Jetzt werden wir den CHAID-Algorithmus Schritt für Schritt erklären. Davor, wir werden ein wenig über chi_square sprechen.
chi_square
Chi-Cuadrado es una messenDas "messen" Es ist ein grundlegendes Konzept in verschiedenen Disziplinen, , die sich auf den Prozess der Quantifizierung von Eigenschaften oder Größen von Objekten bezieht, Phänomene oder Situationen. In Mathematik, Wird verwendet, um Längen zu bestimmen, Flächen und Volumina, In den Sozialwissenschaften kann es sich auf die Bewertung qualitativer und quantitativer Variablen beziehen. Die Messgenauigkeit ist entscheidend, um zuverlässige und valide Ergebnisse in der Forschung oder praktischen Anwendung zu erhalten.... estadística para encontrar la diferencia entre los nodos secundarios y principales. Um dies zu berechnen, encontramos la diferencia entre los conteos observados y esperados de la VariableIn Statistik und Mathematik, ein "Variable" ist ein Symbol, das einen Wert darstellt, der sich ändern oder variieren kann. Es gibt verschiedene Arten von Variablen, und qualitativ, die nicht-numerische Eigenschaften beschreiben, und quantitative, numerische Größen darstellen. Variablen sind grundlegend in Experimenten und Studien, da sie die Analyse von Beziehungen und Mustern zwischen verschiedenen Elementen ermöglichen, das Verständnis komplexer Phänomene zu erleichtern.... objetivo para cada nodo y la suma al cuadrado de estas diferencias estandarizadas nos dará el valor de Chi-cuadrado.
Formel
Um das dominanteste Merkmal zu finden, Chi-Quadrat-Tests verwenden, die auch als CHAID . bezeichnet werden, während ID3 Informationsgewinne nutzt, C4.5 usa la relación de ganancia y CART usa el IndexDas "Index" Es ist ein grundlegendes Werkzeug in Büchern und Dokumenten, Dies ermöglicht es Ihnen, die gewünschten Informationen schnell zu finden. Allgemein, Sie wird am Anfang einer Arbeit präsentiert und organisiert die Inhalte hierarchisch, mit Kapiteln und Abschnitten. Die richtige Vorbereitung erleichtert die Navigation und verbessert das Verständnis des Materials, was es zu einer unverzichtbaren Ressource sowohl für Studenten als auch für Fachleute in verschiedenen Bereichen macht.... GINI.
Heute, die meisten Programmierbibliotheken (zum Beispiel, Pandas für Python) Verwenden Sie standardmäßig die Metrik von Pearson für die Korrelation.
Die Chi-Quadrat-Formel: –
√ ((Ja – Ja ‚)2 / Ja ‚)
donde y es real y se espera y ‚.
Datensatz
Wir werden Entscheidungsregeln für den folgenden Datensatz erstellen. Die Entscheidungsspalte ist das Ziel, das wir anhand einiger Merkmale finden möchten.
Übrigens, Wir ignorieren die Tagesspalte, da es sich nur um die Zeilennummer handelt.
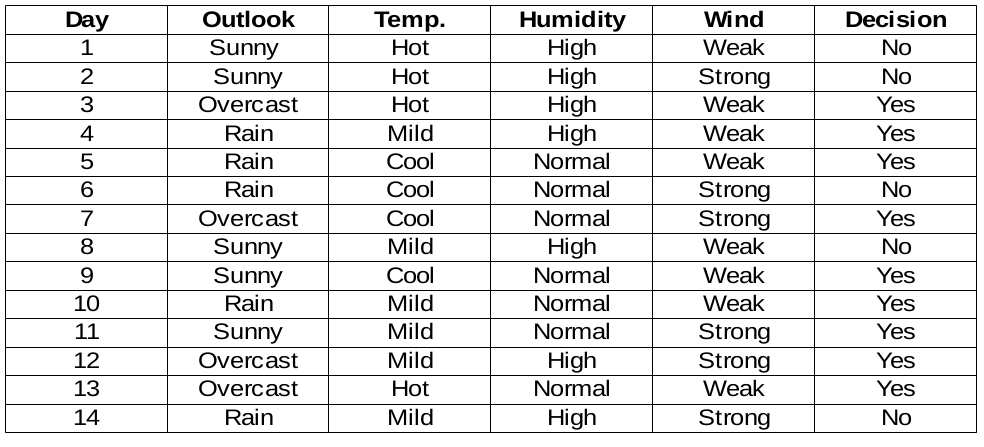
um das Python-Implementierungs-Dataset aus der CSV-Datei unten zu lesen: –
Pandas als pd importieren
data = pd.read_csv("dataset.csv")
daten.kopf()
Wir müssen das wichtigste Merkmal in den Zielspalten finden, um den Knoten zum Aufteilen der Daten in diesem Datensatz auszuwählen.
Feuchtigkeitscharakteristik
Es gibt zwei Arten der Klasse, die in den Feuchtigkeitsspalten vorhanden sind: groß und normal. Jetzt berechnen wir die chi_square-Werte für sie.
| Jawohl | Nein | Gesamt | Erwartet | Chi-Quadrat Ja | Chi-Quadrat Nr | |
| Hoch | 3 | 4 | 7 | 3,5 | 0,267 | 0,267 |
| niedrig | 6 | 1 | 7 | 3,5 | 1.336 | 1.336 |
Für jede Reihe, die Summenspalte ist die Summe der Ja- und Nein-Entscheidungen. Die Hälfte der Gesamtspalte wird als Erwartungswert bezeichnet weil da 2 Klassen in Entscheidung. Anhand dieser Tabelle lassen sich die Chi-Quadrat-Werte leicht berechnen..
Zum Beispiel,
Chi-Quadrat ja für hohe Luftfeuchtigkeit ist √ ((3– 3,5)2 / 3,5) = 0,267
während der echte ist 3 und das erwartete ist 3,5.
Dann, der Chi-Quadrat-Wert der Feuchtekennlinie ist
= 0,267 + 0,267 + 1,336 + 1,336
= 3.207
Jetzt, wir finden auch Chi-Quadrat-Werte für andere Merkmale. Das Merkmal mit dem maximalen Chi-Quadrat-Wert ist der Entscheidungspunkt. Was ist mit der Windfunktion?
Windcharakteristik
Es gibt zwei Arten der Klasse, die in den Windspalten vorhanden sind: schwach und stark. Die folgende Tabelle ist die folgende Tabelle.
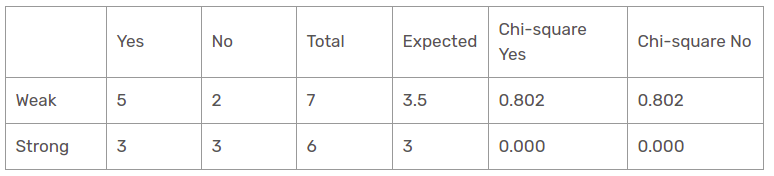
Hier, der Chi-Quadrat-Testwert der Windkennlinie ist
= 0,802 + 0,802 + 0 + 0
= 1,604
Dies ist auch ein Wert kleiner als der Chi-Quadrat-Wert der Luftfeuchtigkeit. Was ist mit der Temperaturfunktion?
Temperaturcharakteristik
Es gibt drei Arten der Klasse, die in den Temperaturspalten vorhanden sind: heiße, kalt und glatt. Die folgende Tabelle ist die folgende Tabelle.
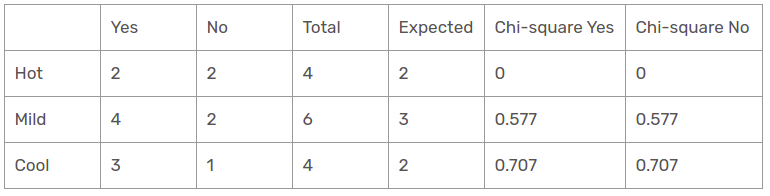
Hier, der Chi-Quadrat-Testwert der Temperaturkennlinie ist
= 0 + 0 + 0,577 + 0,577 + 0,707 + 0,707
= 2.569
Dies ist ein Wert kleiner als der Chi-Quadrat-Wert der Luftfeuchtigkeit und auch größer als der Chi-Quadrat-Wert des Windes. Was ist mit der Outlook-Funktion??
Outlook-Funktion
Es gibt drei Arten von Klassen in den Temperaturspalten: sonnig, regnerisch und bewölkt. Die folgende Tabelle ist die folgende Tabelle.
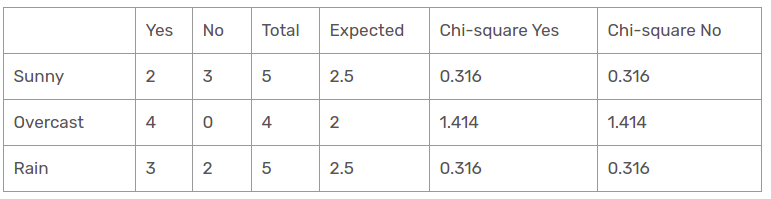
Hier, der Wert des Chi-Quadrat-Tests der Perspektivenfunktion ist
= 0,316 + 0,316 + 1,414 + 1,414 + 0,316 + 0,316
= 4.092
Wir haben die Chi-Quadrat-Werte aller Merkmale berechnet. Lass uns sie alle an einem Tisch sehen.
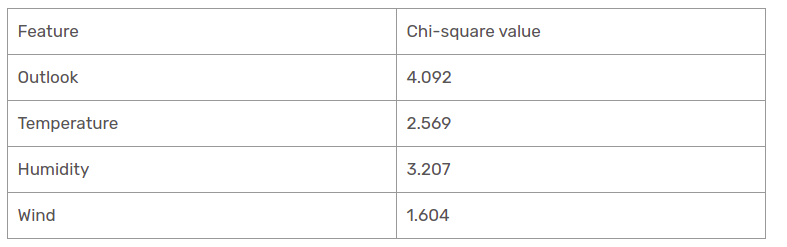
Wie es aussieht, die Outlook-Spalte hat den höchsten und höchsten Chi-Quadrat-Wert. Dies impliziert, dass es das Hauptmerkmal der Komponente ist. Zusammen mit diesen Werten, Wir werden dieses Feature im Root-Knoten platzieren.
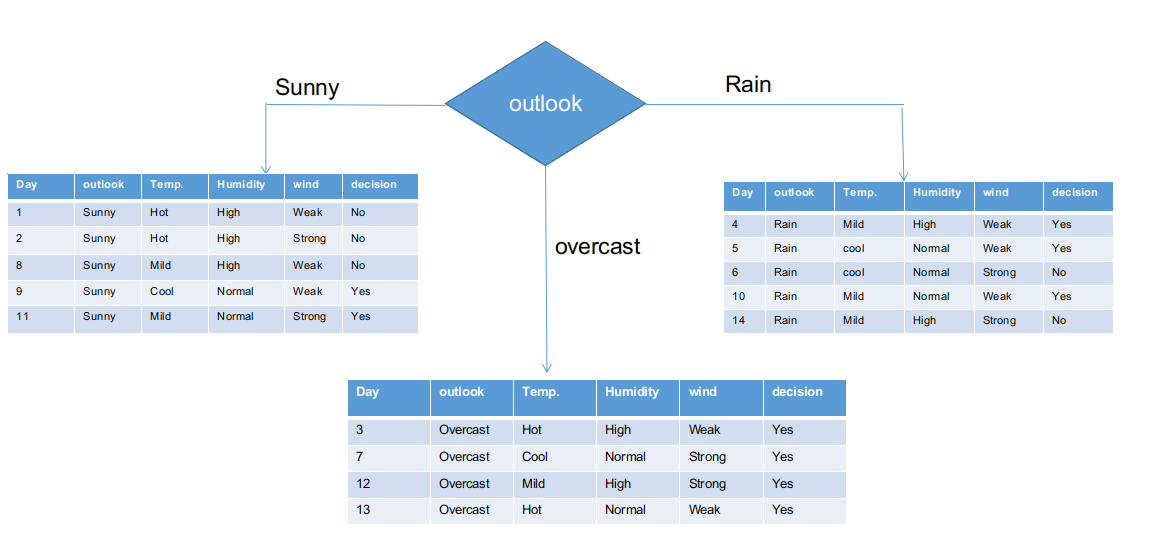
Wir haben die Rohinformationen basierend auf den Outlook-Klassen in der obigen Abbildung getrennt. Zum Beispiel, der getrübte Zweig hat einfach eine positive Entscheidung über den Subinformationsdatensatz. Dies impliziert, dass der CHAID-Baum JA zurückgibt, wenn das Panorama bewölkt ist.
Sowohl sonnige als auch regnerische Äste haben Ja- und Nein-Entscheidungen. Wir werden Chi-Quadrat-Tests für diese subinformativen Datensätze anwenden.
Ausblick = sonniger Zweig
Diese Filiale hat 5 Beispiele. Heutzutage, wir suchen das vorherrschende Merkmal. Übrigens, Wir werden die Outlook-Funktion jetzt ignorieren, da sie völlig gleich sind. Am Ende des Tages, Wir finden die vorherrschenden Spalten zwischen Temperatur, Feuchtigkeit und Wind.
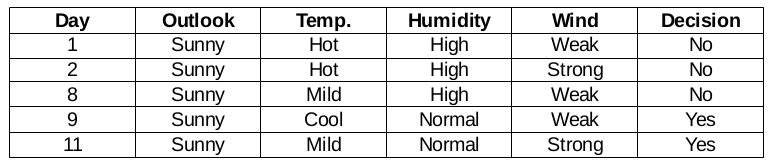
Feuchtefunktion bei sonnigem Panorama
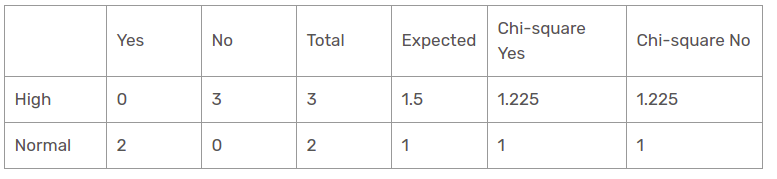
Der Chi-Quadrat-Wert der Luftfeuchtigkeitscharakteristik für eine sonnige Perspektive ist
= 1,225 + 1,225 + 1 + 1
= 4.449
Windfunktion bei sonnigem Panorama
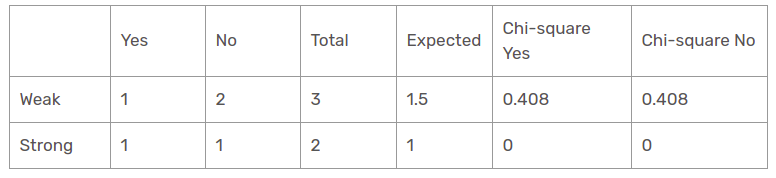
Der Chi-Quadrat-Wert der Windcharakteristik für die sonnige Perspektive ist
= 0,408 + 0,408 + 0 + 0
= 0,816
Temperaturfunktion bei sonnigem Panorama
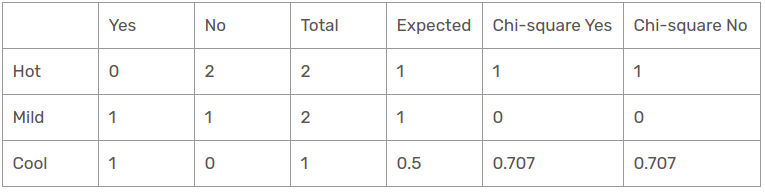
Dann, der Chi-Quadrat-Wert der Temperaturkennlinie für die sonnige Perspektive ist
= 1 + 1 + 0 + 0 + 0,707 + 0,707
= 3.414
Wir haben Chi-Quadrat-Werte für die sonnige Perspektive gefunden. Lass uns sie alle an einem Tisch sehen.
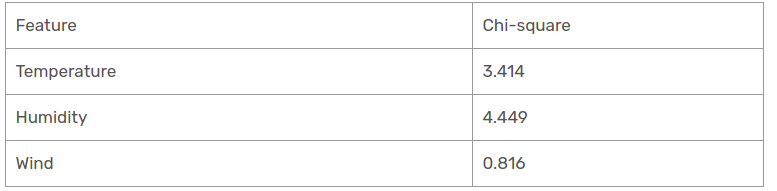
Heutzutage, Luftfeuchtigkeit ist das vorherrschende Merkmal des sonnigen Pavillonzweigs. Wir werden diese Eigenschaft als Entscheidungsregel verwenden.
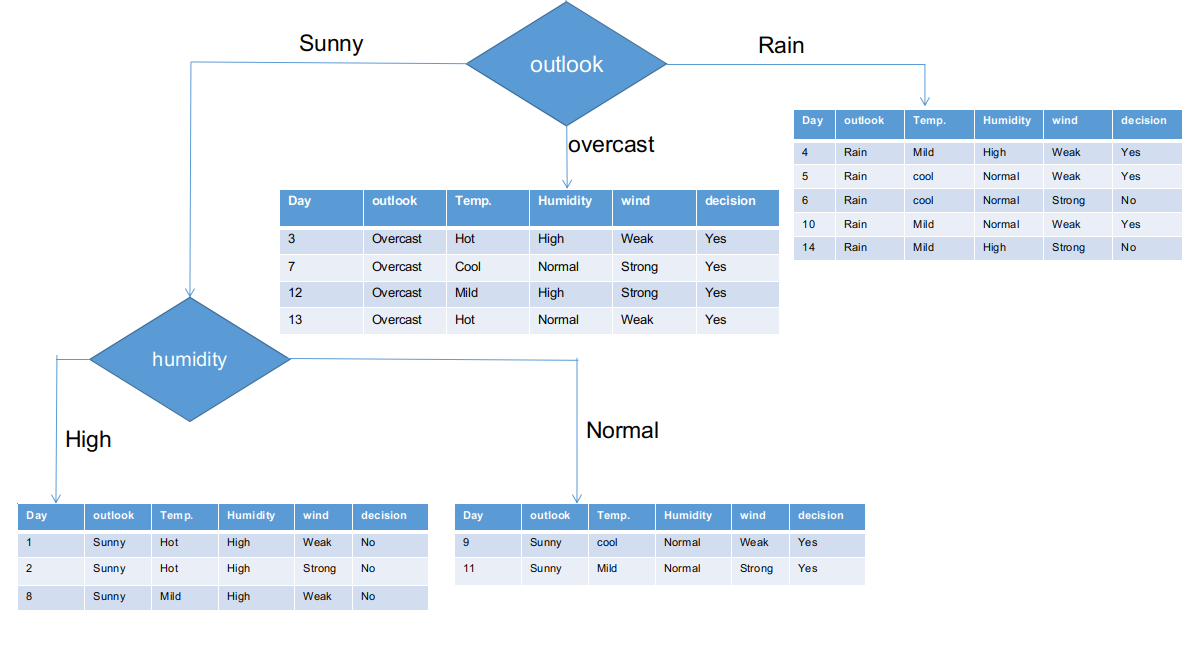
Heutzutage, beide Feuchtezweige für die sonnige Perspektive haben nur eine Entscheidung wie oben beschrieben. Der CHAID-Baum gibt NEIN für eine sonnige Perspektive und hohe Luftfeuchtigkeit und JA für eine sonnige Perspektive und normale Luftfeuchtigkeit zurück.
Regenperspektive Zweig
In Wirklichkeit, dieser Zweig hat sowohl positive als auch negative Entscheidungen. Wir müssen den Chi-Quadrat-Test für diesen Zweig anwenden, um eine genaue Entscheidung zu treffen. Diese Filiale hat 5 verschiedene Instanzen, wie im beigefügten Datensatz zur Erfassung von Unterinformationen gezeigt. Wie wäre es, wenn wir das vorherrschende Merkmal zwischen der Temperatur herausfinden, Feuchtigkeit und Wind?
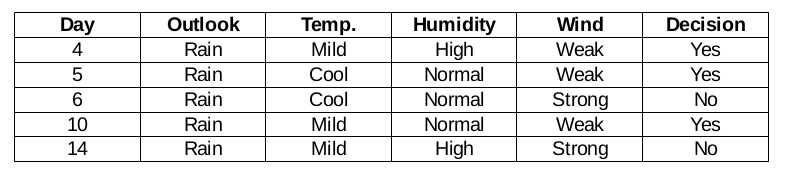
Windfunktion für Regenvorhersage
Es gibt zwei Arten einer Klasse, die in der Windcharakteristik für die Regenperspektive vorhanden ist: schwach und stark.
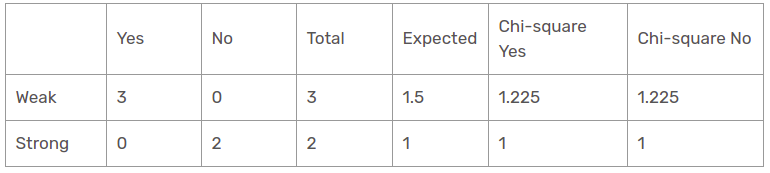
Dann, der Chi-Quadrat-Wert der Windcharakteristik für die Regenperspektive ist
= 1,225 + 1,225 + 1 + 1
= 4.449
Feuchtefunktion für Regenvorhersage
Es gibt zwei Arten von Klassen, die in der Feuchtigkeitscharakteristik für die Regenperspektive vorhanden sind: groß und normal.
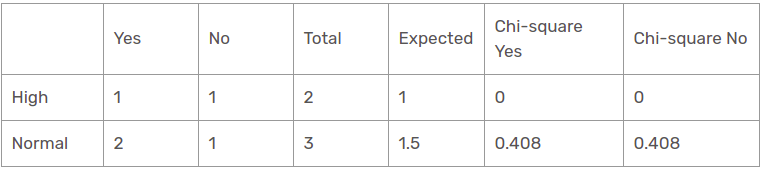
Der Chi-Quadrat-Wert der Feuchtekennlinie für die Regenperspektive ist
= 0 + 0 + 0.408 + 0.408
= 0,816
Temperaturverlauf für Regenvorhersage
Es gibt zwei Arten von Klassen in den Temperatureigenschaften für die Regenperspektive, wie warm und kühl.

Der Chi-Quadrat-Wert der Temperaturkennlinie für die Regenperspektive ist
= 0 + 0 + 0.408 + 0.408
= 0,816
Wir haben festgestellt, dass alle Chi-Quadrat-Werte für Regen der Perspektivzweig sind. Sehen wir sie alle an einem Tisch.
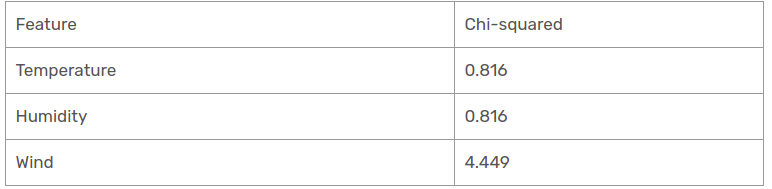
Deswegen, Die Windfunktion ist der Gewinner des Regens ist der Zweig der Perspektive. Fügen Sie diese Spalte in den verbundenen Zweig ein und sehen Sie sich den entsprechenden subinformativen Datensatz an.
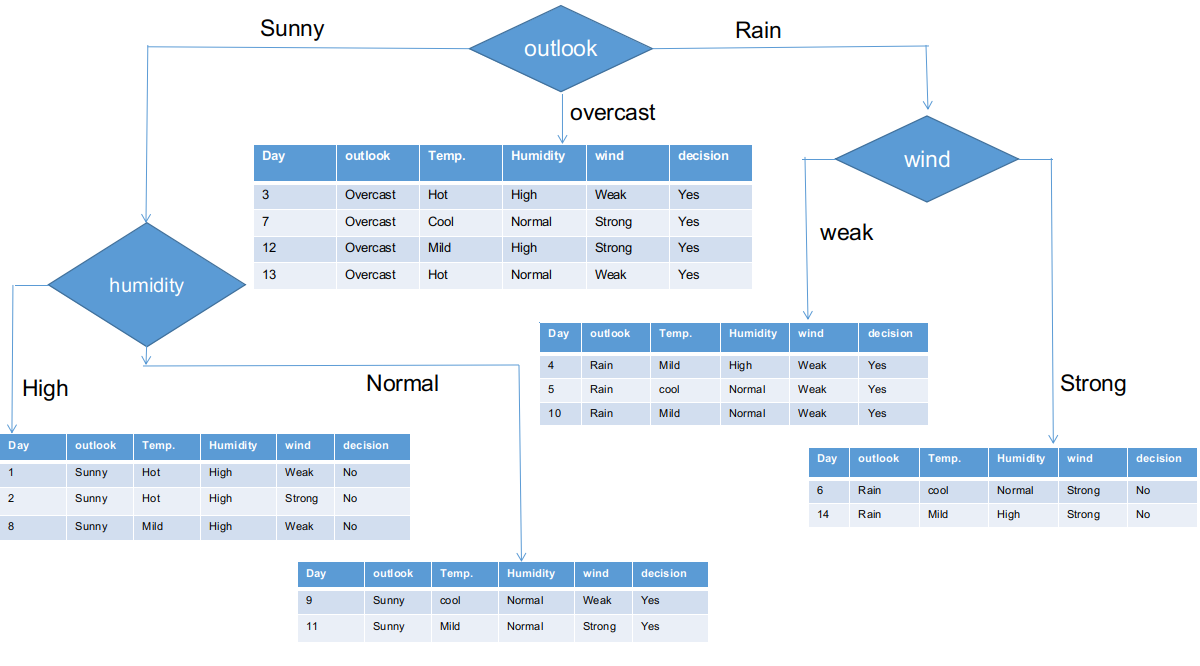
Wie es aussieht, alle Filialen haben subinformative Datensätze mit einer einzigen Entscheidung, wie ja oder nein. Diesen Weg, wir können den CHAID-Baum wie unten dargestellt generieren.
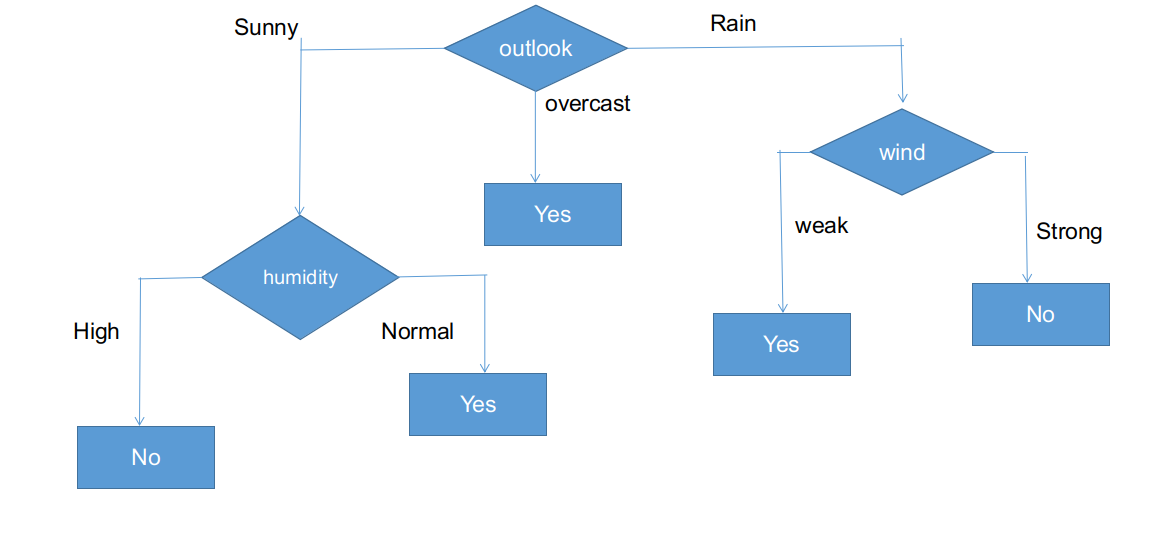
Die endgültige Form des CHAID-Baumes.
Python-Implementierung eines Entscheidungsbaums mit CHAID
von chefboost importiere Chefboost als cb
Pandas als pd importieren
data = pd.read_csv("/home/kajal/Downloads/weather.csv")
daten.kopf()
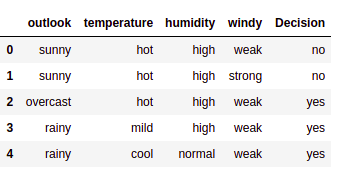
config = {"Algorithmus": "CHAID"}
Baum = cb.fit(Daten, Konfiguration)
Baum
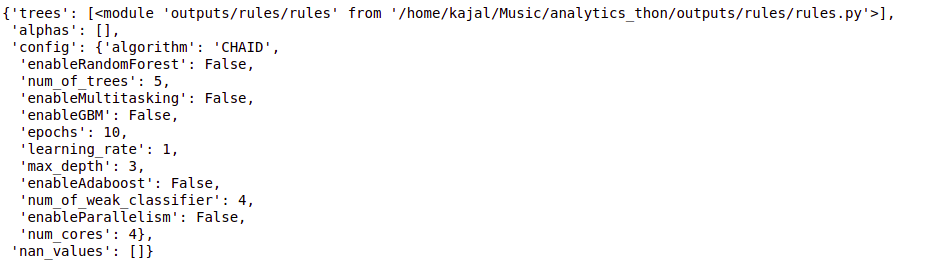
# test_instance = ['sonnig','heiße','hoch','schwach','Nein'] test_instance = data.iloc[2] test_instanz
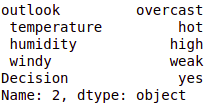
cb.vorhersagen(Baum,test_instanz)
Ausgang:- 'Jawohl'
#obj[0]: Ausblick, obj[1]: Temperatur, obj[2]: Feuchtigkeit, obj[3]: windig
# {"Besonderheit": "Ausblick", "Instanzen": 14, "metrischer_wert": 4.0933, "Tiefe": 1}
def findEntscheidung(obj):
wenn obj[0] == 'regnerisch':
# {"Besonderheit": " windig", "Instanzen": 5, "metrischer_wert": 4.4495, "Tiefe": 2}
wenn obj[3] == 'schwach':
return 'yes'
elif obj[3] == 'stark':
return 'no'
else:
return 'no'
elif obj[0] == 'sonnig':
# {"Besonderheit": " Feuchtigkeit", "Instanzen": 5, "metrischer_wert": 4.4495, "Tiefe": 2}
wenn obj[2] == 'hoch':
return 'no'
elif obj[2] == 'normal':
return 'yes'
else:
return 'yes'
elif obj[0] == 'bewölkt':
return 'yes'
else:
'Ja' zurückgeben
Fazit
Deswegen, Wir haben in diesem Beitrag einen CHAID-Entscheidungsbaum von Grund auf neu erstellt. CHAID verwendet eine Chi-Quadrat-Messmetrik, um das wichtigste Merkmal zu entdecken und es rekursiv anzuwenden, bis subinformative Datensätze eine einzige Entscheidung haben. Obwohl es sich um einen Legacy-Entscheidungsbaumalgorithmus handelt, es ist immer noch der gleiche Prozess für Sortierprobleme.
Die in diesem Artikel gezeigten Medien sind nicht Eigentum von DataPeaker und werden nach Ermessen des Autors verwendet.






