Cet article a été publié dans le cadre du Blogathon sur la science des données

introduction
Apprentissage. La régression logistique est généralement utilisée lorsque nous devons classer les données en deux ou plusieurs classes. L'un est binaire et l'autre est la régression logistique à classes multiples. Comme le nom le suggère, la classe binaire a 2 des cours qui sont Oui / Non, Vrai / Faux, 0/1, etc. Dans la classification de plusieurs classes, il y a plus de 2 classes pour classer les données. Mais, avant de partir, définissons d'abord la régression logistique:
“La régression logistique est un algorithme de classification pour les variables catégorielles telles que Oui / Non, Vrai / Faux, 0/1, etc.”
En quoi diffère-t-elle de la régression linéaire?
Vous avez peut-être aussi entendu parler de la régression linéaire. Laissez-moi vous dire qu'il y a une grande différence entre la régression linéaire et la régression logistique. La régression linéaire est utilisée pour générer des valeurs continues telles que le prix de la maison, le revenu, la population, etc. Dans la régression logistique, on calcule généralement la probabilité qui se situe entre l'intervalle 0 Oui 1 (tous les deux inclus). Ensuite, la probabilité peut être utilisée pour classer les données. Par exemple, si la probabilité calculée s'avère supérieure à 0,5, alors les données appartenaient à la classe A et, au contraire, pour moins de 0,5, les données appartenaient à la classe B.
Mais ma question est de savoir si nous pouvons toujours utiliser la régression linéaire pour la classification. Ma réponse sera "Oui!! Pourquoi pas? Mais c'est sûr que c'est une idée absurde". Ma raison sera que vous pouvez attribuer une valeur seuil pour la régression linéaire, c'est-à-dire, si la valeur prédite est supérieure à la valeur seuil, appartenait à la classe A; au contraire, à la classe B. Mais cela donnera une grosse erreur et un mauvais modèle avec une faible précision, qu'on ne veut vraiment pas. Droite? Je vous suggère d'utiliser uniquement des algorithmes de tri.
Regardons maintenant le graphique de régression linéaire ci-dessous.
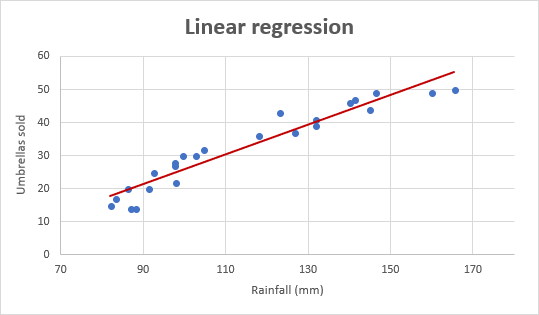
(Courtoisie: https://www.ablebits.com/)
Le graphique est une ligne droite qui passe par certains points car nous évitons toujours les courbes de surajustement et de décalage.
Regardons maintenant le graphique de régression logistique:
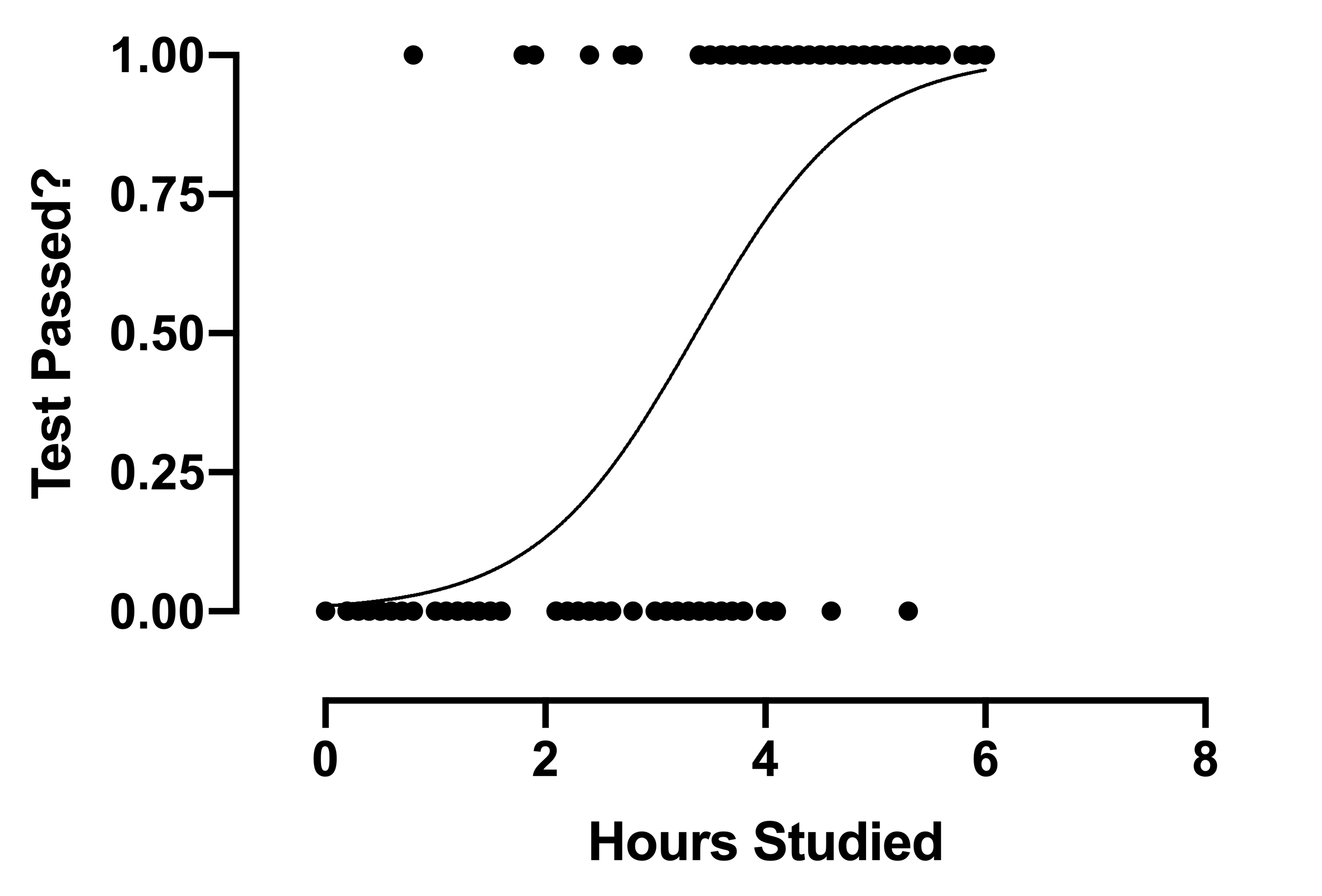
Le graphique est une ligne courbe au lieu d'une ligne droite, contrairement à la régression linéaire.
C'est une grande différence entre les deux types de régression dont nous venons de parler.. Alors ma prochaine question est.
Pourquoi avons-nous une ligne courbe pour la régression logistique au lieu d'une ligne droite?
Pour répondre à cette question, nous allons parcourir un peu la régression linéaire et à partir de là, nous arriverons à la courbe de régression logistique. Ça c'est bien? Nous allons commencer.
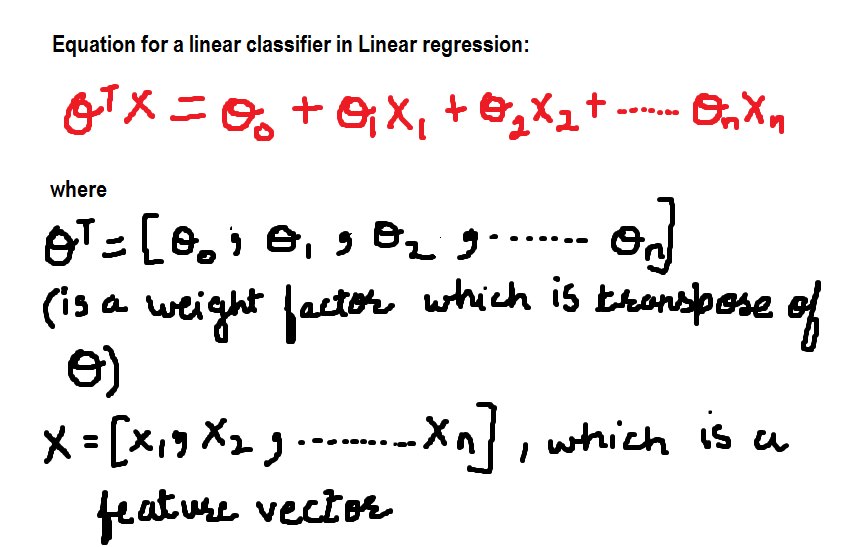
Pour l'instant, l'équation du classificateur linéaire est:
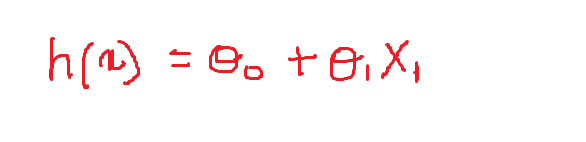
Nous allons maintenant définir les valeurs des poids variables:
theta_0 = -1 et thêta = 0.1
Ensuite, Notre équation ressemble à ceci et ce qui suit est le graphique qui représente l'équation dans le plan 2-D:
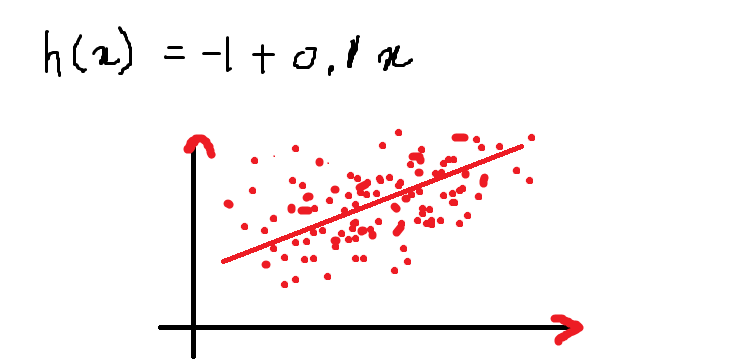
Ci-dessus est une équation d'une ligne pour l'équation donnée:
h (X) = – 1 + 0.1X
La valeur de la fonction h (X) quand x = 13 il est:
h (13) = – 1+ (0,1) * (13) = 0,3
Comme décrit plus haut dans cet article, Je suis en train de définir le seuil dans 0.5, qui est une valeur de h supérieure à (égal à) 0.5 sera étiqueté comme 1 Oui, au contraire, 0. Nous pouvons le définir comme suit sous la forme d'une fonction échelonnée:

À présent, d'accord avec ça, h a une valeur de 0.3, d'où la valeur de y_hat = 0 selon la fonction définie ci-dessus.
À présent, Une chose à noter ici est que chaque valeur supérieure à 0.5, supposons que je dise que la valeur de 'h’ il est 1000 pour une valeur de x, alors il sera étiqueté comme 1 seulement, il n'y a pas de différence entre la valeur 1 Oui 1000 puisque les deux sont classés comme 1 seulement. C'est correct? Pouvons-nous accepter cette solution? Bon, non! je ne l'accepterais pas !!!
Une chose plus, Quelle est la probabilité que h ait une valeur de 0.3? Toutes ces questions restent sans réponse. Pour ces raisons, les data scientists ne préfèrent pas utiliser la régression linéaire à des fins de classification.
avant de continuer, Je veux vous montrer comment la fonction y_hat se comporte graphiquement:
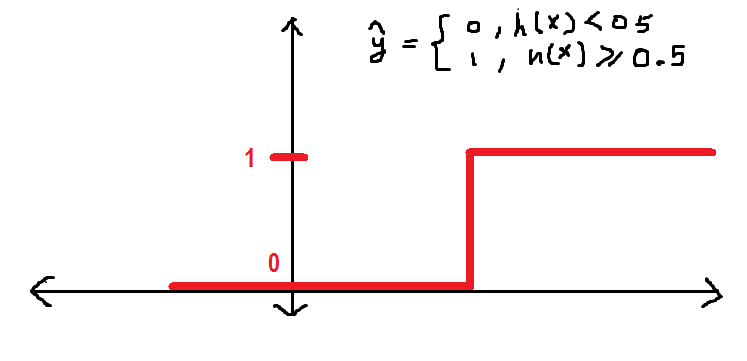
Ce sera mieux si nous avons une courbe plus douce au lieu de ce qui précède. Nous allons voir:
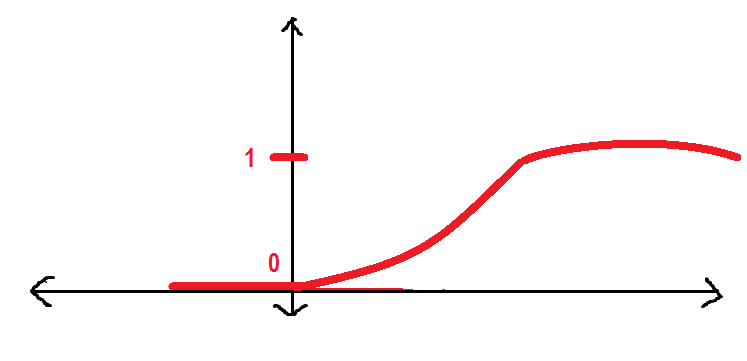
La courbe ci-dessus est appelée Fonction sigmoïde que nous utiliserons tout au long de cet article. Ici, je vais présenter la fonction sigmoïde.
Qu'est-ce que la fonction sigmoïde?
La fonction sigmoïde est représentée par le symbole sigma. Son comportement graphique a été décrit dans la figure précédente. L'équation mathématique de la fonction sigmoïde est décrite ci-dessous:
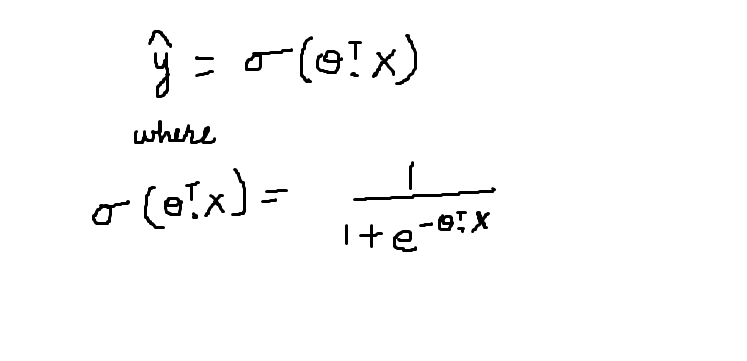
La fonction sigmoïde donne la probabilité que les données appartiennent à une classe particulière qui se trouve dans l'intervalle [0,1]. Accepte le produit scalaire de la transposition de thêta et le vecteur caractéristique X comme paramètre. La valeur résultante est la probabilité.
Donc, lorsque P (Y = 1 | X) = sigmoïde (thêta * X)
P (Y = 0 | X) = 1- sigmoïde (thêta * X)
En outre, Je veux que vous observiez le comportement de la fonction sigmoïde:
- Quand thêta (transposition) * X devient tellement plus grand, la valeur sigmoïde devient égale à 1
- Lorsque thêta (transposition) * X devient très petit la valeur sigmoïde devient égale à 0
Applications de la régression logistique
Dans cette section, Je voudrais discuter de certaines des applications de la régression logistique.
1. Prédire la probabilité qu'une personne ait une crise cardiaque
2. Prédire la propension d'un client à acheter un produit ou à suspendre un abonnement.
3. Prédire la probabilité de défaillance d'un processus ou d'un produit donné.
Avant de terminer cet article, Je veux juste récapituler quand vous devriez utiliser la régression logistique:
- Quand vos données sont binaires: 0/1, Vrai / Faux, Oui / Non
- Lorsque vous avez besoin de résultats probabilistes
- Quand vos données peuvent être séparées linéairement
- Lorsque vous avez besoin de comprendre l'impact de la fonctionnalité.
De nombreux autres algorithmes de classification sont largement utilisés en plus de la régression logistique tels que kNN, arbres de décision, Algorithmes de forêt aléatoire et de clustering en tant que clustering de k-moyennes. Mais la régression logistique est un algorithme largement utilisé et également facile à mettre en œuvre..
Il s'agissait donc de l'algorithme de régression logistique pour les débutants. Nous avons parlé de tout ce que vous devez savoir sur la théorie de la régression logistique. J'espère que vous avez apprécié mon article !!
Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.






