Algorithme KNN | Qu'est-ce que l'algorithme KNN?

Vue d'ensemble:

Cet article de KNN est pour:

Comprendre la représentation et la prédiction de l'algorithme K le plus proche (KNN).

Comprendre comment choisir la valeur K et la métrique de distance.

Méthodes de préparation des données requises et avantages et inconvénients de l'algorithme KNN.

· Implémentation Python et pseudocode.

introduction:

K El algoritmo del vecino más cercano se incluye en la categoría de enseignement superviséL’apprentissage supervisé est une approche d’apprentissage automatique dans laquelle un modèle est formé à l’aide d’un ensemble de données étiquetées. Chaque entrée du jeu de données est associée à une sortie connue, permettre au modèle d’apprendre à prédire les résultats pour de nouvelles entrées. Cette méthode est largement utilisée dans des applications telles que la classification d’images, Reconnaissance vocale et prédiction de tendances, soulignant son importance dans... y se usa para clasificación (plus communément) et régression. C'est un algorithme polyvalent qui est également utilisé pour imputer les valeurs manquantes et rééchantillonner les ensembles de données.. Comme le nom le suggère (K voisin le plus proche), considérer K voisins les plus proches (points de données) pour prédire la classe ou la valeur continue du nouveau point de données.

L'apprentissage de l'algorithme est:

1. Apprentissage basé sur les instances: aquí no aprendemos ponderaciones de los datos de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines.... para predecir la salida (comme dans les algorithmes basés sur des modèles), à la place, nous utilisons des instances d'entraînement complètes pour prédire une sortie de données invisible.

2. Apprentissage paresseux: le modèle n'est pas appris à l'aide des données d'apprentissage auparavant et le processus d'apprentissage est reporté à un moment où la prédiction est demandée dans la nouvelle instance.

3. en paramétrique: Un KNN, il n'y a pas de forme prédéfinie de fonction de mappage.

Comment fonctionne KNN?

1. Début:

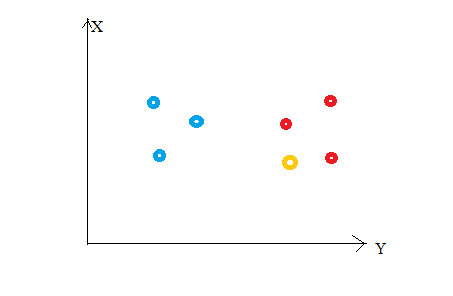
   Considere la siguiente chiffre"Chiffre" est un terme utilisé dans divers contextes, De l’art à l’anatomie. Dans le domaine artistique, fait référence à la représentation de formes humaines ou animales dans des sculptures et des peintures. En anatomie, désigne la forme et la structure du corps. En outre, en mathématiques, "chiffre" Il est lié aux formes géométriques. Sa polyvalence en fait un concept fondamental dans de multiples disciplines..... Disons que nous avons tracé des points de données de notre ensemble d'apprentissage dans un espace de caractéristiques bidimensionnel. Comme on le montre, nous avons un total de 6 points de données (3 rouge et 3 bleu). Les points de données rouges appartiennent à la « classe1’ et les points de données bleus appartiennent à 'class2'. Et le point de données jaune dans un espace d'entités représente le nouveau point pour lequel une classe doit être prédite. Évidemment, nous disons qu'il appartient à "class1’ (Points rouges)

   Parce que?

   Parce que vos voisins les plus proches appartiennent à cette classe !!

   

   Oui, c'est le principe de K Neighbours Neighbours. Ici, les voisins les plus proches sont les points de données qui ont une distance minimale dans l'espace des caractéristiques de notre nouveau point de données. Et K est le nombre de points de données que nous considérons dans notre implémentation de l'algorithme. Donc, la métrique de distance et la valeur K sont deux considérations importantes lors de l'utilisation de l'algorithme KNN. La distance euclidienne est la mesure de distance la plus populaire. Vous pouvez également utiliser la distance de Hamming, la distance de Manhattan, la distance de Minkowski selon vos besoins. Prédire la classe / valeur continue pour un nouveau point de données, considère tous les points de données dans l'ensemble de données d'entraînement. Trouver les voisins les plus proches (points de données) 'K’ des nouveaux points de données de l'espace d'entités et de leurs étiquettes de classe ou valeurs continues.

   Alors:

   Pour le classement: une étiquette de classe attribuée au plus de K voisins les plus proches dans l'ensemble de données d'apprentissage est considérée comme une classe prédite pour le nouveau point de données.

   Pour la régression: la media o médianLa médiane est une mesure statistique qui représente la valeur centrale d’un ensemble de données ordonnées. Pour le calculer, Les données sont organisées de la plus basse à la plus élevée et le numéro au milieu est identifié. S’il y a un nombre pair d’observations, La moyenne des deux valeurs fondamentales est calculée. Cet indicateur est particulièrement utile dans les distributions asymétriques, puisqu’il n’est pas affecté par les valeurs extrêmes.... de los valores continuos asignados a K vecinos más cercanos del conjunto de datos de entrenamiento es un valor continuo predicho para nuestro nuevo punto de datos

2. Représentation du modèle
   

   Ici, nous n'apprenons pas les poids et ne les stockons pas, au lieu de cela, l'ensemble des données d'entraînement est stocké en mémoire. Donc, la représentation du modèle pour KNN est l'ensemble de données d'entraînement complet.

Comment choisir la valeur de K?

K est un paramètre crucial dans l'algorithme KNN. Quelques suggestions pour choisir la valeur K sont:

1. Utilisation des courbes d'erreur: La figure ci-dessous montre les courbes d'erreur pour différentes valeurs K pour les données d'entraînement et de test.

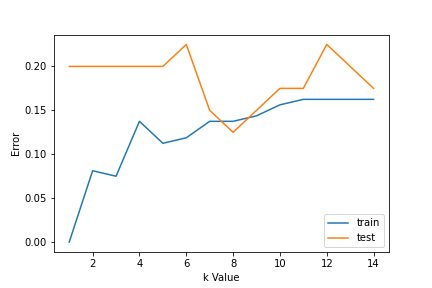
À de faibles valeurs K, il y a un surapprentissage des données / écart élevé. Donc, l'erreur de test est élevée et l'erreur de train est faible. Et K = 1 dans les données du train, l'erreur est toujours nulle, car le voisin le plus proche de ce point est ce point lui-même. Donc, bien que l'erreur d'entraînement soit faible, l'erreur de test est élevée avec des valeurs K inférieures. C'est ce qu'on appelle le surapprentissage.. UNE mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... que aumentamos el valor de K, l'erreur de test est réduite.

Mais après une certaine valeur de K, un biais est introduit / l'inadéquation et l'erreur de test augmentent. Ensuite, on peut dire qu'au départ l'erreur des données de test est élevée (en raison de l'écart), puis il descend et se stabilise et avec une nouvelle augmentation de la valeur de K, augmente encore (en raison de biais). La valeur de K lorsque l'erreur de test se stabilise et est faible est considérée comme la valeur optimale pour K. De la courbe d'erreur ci-dessus, on peut choisir K = 8 pour la mise en œuvre de notre algorithme KNN.

2. En outre, la connaissance du domaine est très utile pour choisir la valeur K.

3. La valeur de K doit être impaire lors de l'examen de la classification binaire (deux classes).

Préparation des données requise:

1. Échelle des données: pour localiser le point de données dans l'espace de caractéristiques multidimensionnel, il serait utile que toutes les fonctionnalités soient à la même échelle. Donc, la standardisationLa normalisation est un processus fondamental dans diverses disciplines, qui vise à établir des normes et des critères uniformes afin d’améliorer la qualité et l’efficacité. Dans des contextes tels que l’ingénierie, Formation et administration, La standardisation facilite la comparaison, Interopérabilité et compréhension mutuelle. Lors de la mise en œuvre des normes, La cohésion est favorisée et les ressources sont optimisées, qui contribue au développement durable et à l’amélioration continue des processus.... o estandarización de los datos ayudará.

2. Réduction de la dimensionnalité: KNN peut ne pas bien fonctionner s'il y a trop de fonctions. Donc, des techniques de réduction de la dimensionnalité telles que la sélection de caractéristiques et l'analyse des composants principaux peuvent être mises en œuvre.

3. Traitement de la valeur manquante: si, à partir de M caractéristiques, il manque des données d'une caractéristique pour un exemple particulier dans l'ensemble d'apprentissage, alors nous ne pouvons pas localiser ou calculer la distance à partir de ce point. Donc, il est nécessaire de supprimer cette ligne ou imputation.

Implémentation Python:

Implémentation de l'algorithme du voisin le plus proche à l'aide de la bibliothèque Scikit-Learn de Python:

Paso 1: obtenir et préparer des données

importer des pandas au format pd
importer numpy en tant que np
importer matplotlib.pyplot en tant que plt
à partir de sklearn.datasets importer make_classification
de sklearn.model_selection importer train_test_split
de sklearn.preprocessing importer StandardScaler
de sklearn.neighbors importer KNeighborsClassifier
à partir des métriques d'importation sklearn

Après le chargement des bibliothèques importantes, nous créons nos données en utilisant sklearn.datasets avec 200 échantillons, 8 caractéristiques et 2 cours. Alors, les données sont réparties dans le train (80%) et tester les données (20%) et sont mis à l'échelle à l'aide de StandardScaler.

X,Y=faire_classement(n_samples= 200,n_features=8,n_informative=8,n_redundant=0,n_repeated=0,n_classes=2,random_state=14)
X_train, X_test, y_train, y_test= train_test_split(X, Oui, test_size=0.2,random_state=32)
sc= StandardScaler()
sc.fit(X_train)
X_train= sc.transform(X_train)
sc.fit(X_test)
X_test= sc.transform(X_test)
X.forme

(200, 8)

Paso 2: Trouver la valeur de K

Pour choisir la valeur K, nous utilisons des courbes d'erreur et une valeur K avec une variance optimale, et l'erreur de biais est choisie comme valeur K à des fins de prédiction. Avec la courbe d'erreur tracée ci-dessous, on choisit K = 7 pour la prédiction

erreur1= []
erreur2= []
pour k dans la plage(1,15):
    knn= KNeighborsClassifier(n_voisins=k)
    knn.fit(X_train,y_train)
    y_pred1= knn.predict(X_train)
    erreur1.append(np.moyenne(y_train!= y_pred1))
    y_pred2= knn.predict(X_test)
    error2.append(np.moyenne(y_test!= y_pred2))
# plt.figure(taille de figue(10,5))
plt.plot(gamme(1,15),erreur1, étiquette="former")
plt.plot(gamme(1,15),erreur2, étiquette="test")
plt.xlabel('Valeur k')
plt.ylabel('Erreur')
plt.légende()

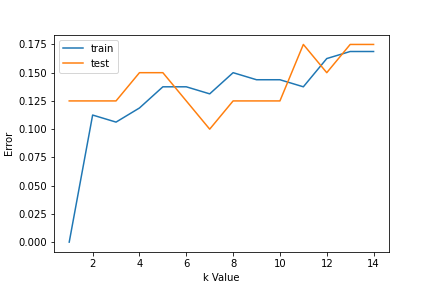
Paso 3: Prédire:

Au pas 2, nous avons choisi que la valeur de K est 7. Maintenant, nous substituons cette valeur et obtenons le score de précision = 0,9 pour les données de test.

knn= KNeighborsClassifier(n_voisins=7)
knn.fit(X_train,y_train)
y_pred= knn.predict(X_test)
metrics.accuracy_score(y_test,y_pred)

0.9

Pseudocode pour K voisin le plus proche (classification):

En rapport