Analyse des composants principaux | Guide d'analyse en composantes principales

Table des matières

• introduction

• Aperçu fluide

• Inconvénients de l'utilisation du PCA

• Exemple pratique

• conclusion

introduction

“L'intelligence artificielle est la dernière invention que l'humanité devra faire". La citation indique clairement que l'apprentissage automatique est l'avenir et de grandes opportunités et avantages pour tous. Que ce soit un nouveau départ pour vous d'apprendre un algorithme vraiment cool en apprentissage automatique.

Comme tout le monde le sait, nous rencontrons souvent des problèmes de stockage et de traitement de données volumineuses dans les tâches d'apprentissage automatique, car il s'agit d'un processus long et des difficultés surgissent également dans l'interprétation. Toutes les fonctionnalités de données ne sont pas nécessaires pour les prédictions. Ces données bruyantes peuvent entraîner de mauvaises performances et un surajustement du modèle.. A travers cet article, laissez-moi vous présenter une technique d'apprentissage non supervisé de l'ACP (Analyse des composants principaux) qui peut vous aider à traiter efficacement ces problèmes dans une certaine mesure et fournir des résultats de prédiction plus précis.

Le PCA a été inventé au début du 20e siècle par Karl Pearson, analogue à théorème de l'axe principal en mécanique et est largement utilisé. Grâce à cette méthode, nous transformons en fait les données en une nouvelle coordonnée, où celui avec la plus grande variance est la composante principale principale. Nous fournissant ainsi les meilleures représentations de données possibles.

Résumé doux

Les données riches en fonctionnalités peuvent contenir des corrélations et des duplications. Ensuite, une fois que vous obtenez les données, l'étape principale consiste à les nettoyer en supprimant les fonctionnalités non pertinentes et en appliquant des techniques d'ingénierie des fonctionnalités qui peuvent même fournir de meilleurs résultats que les fonctionnalités d'origine. Analyse des composants principaux (APC) est l'une de ces techniques par lesquelles la réduction de dimensionnalité est possible (transformation linéaire des attributs existants) et analyse multivariée. Il a plusieurs avantages, y compris la réduction de la taille des données (donc, exécution plus rapide), de meilleures visualisations avec moins de dimensions, maximiser la variance, réduit le surapprentissage, etc.

La composante principale signifie en fait les séquences de vecteurs de direction qui diffèrent en fonction des lignes de meilleur ajustement. On peut également affirmer que ces composants sont des vecteurs propres de la matrice de covariance. Nous examinerons ce concept ci-dessous..

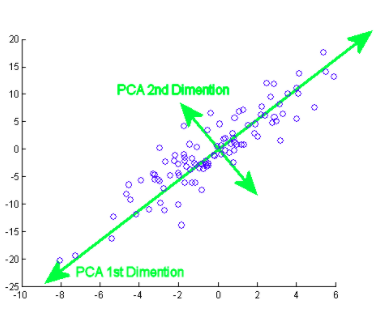
Comment se fait ceci? Initialement, necesitas encontrar los componentes principales desde diferentes puntos de vista durante la fase de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines...., de ceux que vous prenez les composants importants et les moins corrélés et ignorez le reste d'entre eux, réduisant ainsi la complexité. Le nombre de composants principaux peut être inférieur ou égal au nombre total d'attributs.

Supposons que deux colonnes X et Y soient les 2 fonctionnalités,

XY

1 4

2 3

3 4

4 6

5 8

Vouloir dire

X'= 3, Oui’ = 5

Covarianza

les (X, Oui) = (Xi – X ') (Yi – ET') / m – 1, où je = 1 un

C = [ les(X,X) les (X,Oui) ]
[les(Oui,X) les(Oui,Oui) ]

de la même manière, pour plus de fonctionnalités, on trouve la matrice de covariance complète avec plus de dimensions. En continuant à calculer les valeurs propres, vecteur, etc., nous pouvons trouver les principaux composants. L'importation d'algorithmes et l'utilisation de bibliothèques exactes facilitent l'identification des composants sans calculs / opérations manuelles. Notez que le nombre de valeurs propres / Les vecteurs propres vous donneront le nombre de dimensions et la quantité de variance associée à ces composants.

Maintenant bien, car il y a de nombreux composants majeurs au big data, est sélectionné principalement sur la base de laquelle représente la plus grande variation possible. Par conséquent, les composantes suivantes sont également décidées par ordre décroissant de variance des composantes précédentes en ordonnant les valeurs propres, tant que ceux-ci n'ont pas non plus de corrélation avec les composants principaux précédents. Ensuite, nous rejetons les composants avec moins de valeurs propres / vecteur (moins important).

Dans la dernière étape, nous utilisons des vecteurs de caractéristiques pour orienter les données vers celles représentées par les composants principaux (Analyse des composants principaux). Ceci est fait en multipliant la transposition de l'ensemble de données d'origine par la transposition du vecteur de caractéristiques.

Inconvénients de l'utilisation du PCA / Désavantages

Vous devez savoir que la normalisation des données (qui inclut également la conversion de variables catégorielles en variables numériques) est un must avant d'utiliser PCA. Lors de l'application du PCA, les caractéristiques indépendantes deviennent moins interprétables car ces composants principaux ne sont pas non plus lisibles ou interprétables. Il y a aussi des chances que vous perdiez des informations pendant l'ACP.

Exemple pratique

À présent, voyons comment un algorithme est implémenté dans un ensemble de données. Je vais vous guider pas à pas à travers chaque partie du code.

Jette un coup d'œil à cet ensemble de données. C'est le célèbre jeu de données de fleurs IRIS, contenant des caractéristiques telles que la longueur des sépales, longueur des pétales, la largeur du sépale et la largeur du pétale, et la variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... objetivo es la especie. Ce que vous entendez par variable cible est la valeur / classe que vous devez prévoir, qui dans ce cas est le genre d'espèce à laquelle appartient la fleur.

la source: Wikipédia

Importation d'ensembles de données et de bibliothèques de base

En premier lieu, commençons par importer les bibliothèques nécessaires,

importer numpy en tant que np
importer des pandas au format pd
importer matplotlib.pyplot en tant que plt
à partir de sklearn.datasets importer load_iris

Chargez les données et affichez les noms des caractéristiques et des classes pour votre compréhension,

iris = load_iris()
#Noms des fonctionnalités et codage des variables cibles
imprimer(iris.feature_names)
imprimer(iris.target_names)
données = pd.DataFrame(iris.data)
data.columns = iris.feature_names
Les données['CLASSER'] = iris.cible
data.head()

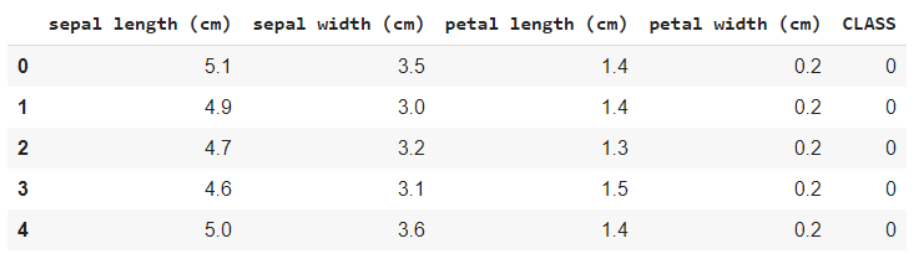
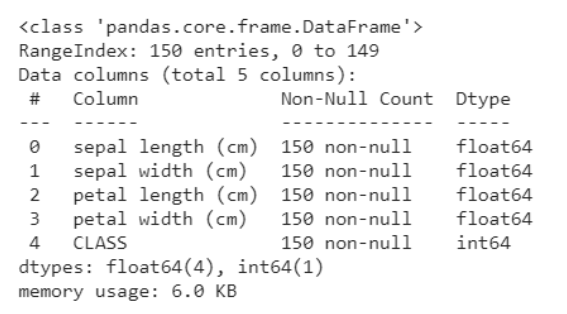
L'extrait de code suivant vous aide à obtenir une analyse des données, à savoir combien de variables sont catégorielles et combien sont numériques. En outre, il est clair ci-dessous que toutes les lignes ne sont pas nulles, en cas d'objets nuls, nous obtenons le nombre et les lignes / colonnes dans lesquelles ils sont présents. Cela nous aide à suivre les étapes de prétraitement pour nettoyer les données.

data.info()

La fonction data.describe () fournit généralement une description statistique de l'ensemble de données. Ceux-ci pourraient être bénéfiques à bien des égards, vous pouvez utiliser ces données pour compléter les valeurs manquantes ou créer une nouvelle caractéristique, et beaucoup plus.

données.décrire()

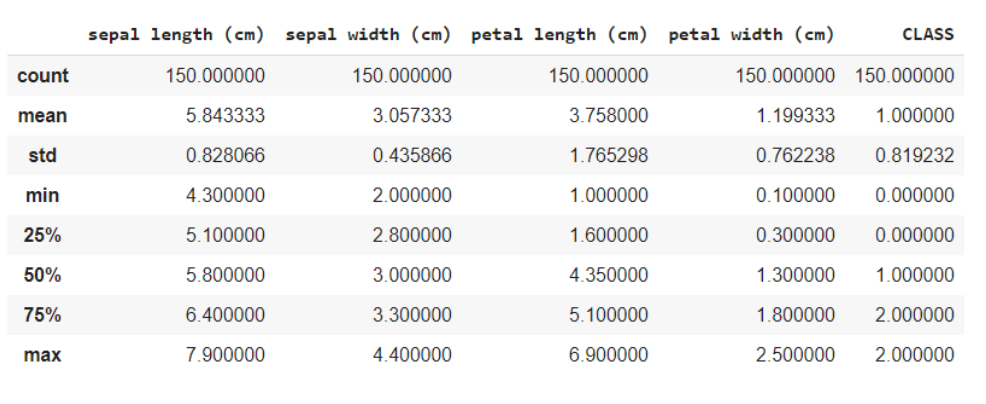
Ici, vous divisez les données en caractéristiques et en variables cibles comme X et et respectivement. Et lors de l'utilisation de la méthode de forme, sait que les données ont 150 rangées et 5 colonnes au total, desquelles 1 la colonne est votre variable cible et d'autres 4 sont les caractéristiques / les attributs.

x = données.iloc[:,:4]  #caractéristiques
y = data.iloc[:,4] #cible
x.forme, y.forme

Dehors: ((150, 4), (150,))

Puisque toutes les caractéristiques sont numériques, c'est facile pour le modèle pour la formation. Si les données contenaient des variables catégorielles, nous devons d'abord les convertir en numérique, puisque les machines / les ordinateurs peuvent mieux gérer les nombres.

Importation de la bibliothèque PCA

de sklearn.decomposition importer PCA
PCA = PCA()
X = pca.fit_transform(X)
pca.get_covariance()

Explained_variance=pca.explained_variance_ratio_
expliqué_variance

Visualisations

avec plt.style.context('dark_background'):
    plt.figure(taille de la figue=(6, 4))
    plt.bar(gamme(4), expliqué_variance, alpha=0,5, align='centre',
            étiquette="variance expliquée individuelle")production
    plt.ylabel(« Rapport de variance expliqué »)
    plt.xlabel('Composants principaux')
    plt.légende(loc ="meilleur")
    plt.tight_layout()

A partir des visualisations, on obtient l'intuition qu'il n'y a principalement que 3 composants avec une variance significative, donc, nous sélectionnons le nombre de composants principaux comme 3.

PCA = PCA(n_composants=3)
X = pca.fit_transform(X)

Essai de train fractionné

La division des essais de train est une méthode courante de formation et d'évaluation. Comme d'habitude, les prédictions sur les données entraînées elles-mêmes peuvent conduire à un surapprentissage, donnant ainsi de mauvais résultats pour des données inconnues. Dans ce cas, en divisant les données en ensembles d'apprentissage et de test, vous vous entraînez puis prédisez à l'aide du modèle dans 2 différents ensembles, résolvant ainsi le problème du surapprentissage.

de sklearn.model_selection importer train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Oui, taille_test = 0.3, état_aléatoire=20, stratifier=y)

Formation de modèle

Notre objectif est d'identifier la classe / espèce à laquelle appartient la fleur compte tenu de certaines de ses caractéristiques. Donc, c'est un problème de classification et le modèle que nous utilisons utilise K plus proches voisins.

de sklearn.neighbors importer KNeighborsClassifier
modèle = KNeighborsClassifier(7)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)

Prédictions

à partir de sklearn.metrics importer confusion_matrix
de sklearn.metrics importer precision_score
cm = confusion_matrice(y_test, y_pred)  #matrice de confusion
imprimer(cm)
imprimer(score_précision(y_test, y_pred))

La matrice de confusion vous montrera le nombre de faux positifs, faux négatifs, vrais positifs et vrais négatifs.

La puntuación de precisión le indicará en qué mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... nuestro modelo ha sido eficaz a la hora de ofrecer predicciones para nuevos datos. Le 97% c'est une très bonne note, et c'est pourquoi nous pouvons dire que le nôtre est un bon modèle.

Vous pouvez voir le code complet sur cette collaboration google prévu.

conclusion

J'espère vraiment que vous avez eu une intuition sur PCA et que vous connaissez également l'exemple discuté ci-dessus. Ce n'est pas si compliqué à digérer, reste juste concentré. Assurez-vous de lire ceci une fois de plus si vous le trouvez utile et développez vous-même l'algorithme pour mieux le comprendre..

Passez une bonne journée !! 🙂

En rapport