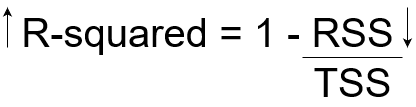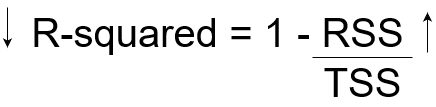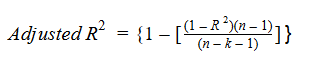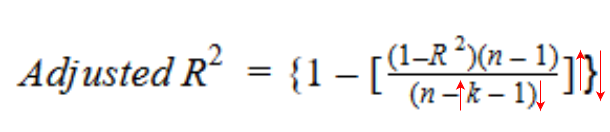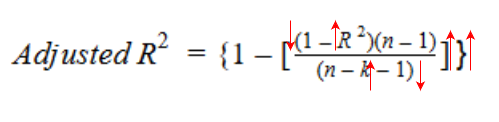Vue d'ensemble
- Comprendre le concept de R carré et R carré
- Découvrez les principales différences entre R-carré et R-carré ajusté
introduction
Quand j’ai commencé mon parcours en science des données, le premier algorithme que j’ai exploré était la régression linéaire. Après avoir compris les concepts de régression linéaire et le fonctionnement de l’algorithme, était vraiment excité de l’utiliser et de faire des prédictions sur un énoncé de problème. Je suis sûr que la plupart d’entre vous auraient fait la même chose.. Mais une fois que nous avons prédit les valeurs, suivant?
Vient ensuite la partie délicate. Une fois que nous avons construit notre modèle, l’étape suivante consistait à évaluer leur rendement. Inutile de dire que la tâche d’évaluer le modèle est fondamentale et met en évidence les lacunes de notre modèle.. Choisir le plus approprié Métrique d'évaluation est une tâche cruciale. Et j’ai trouvé deux mesures importantes.: R-carré et R-carré ajustés en dehors de MAE / MSE / RMSE. Quelle est la différence entre les deux?? Lequel devrais-je utiliser?
R carré et R carré sont deux de ces mesures d’évaluation qui peuvent sembler déroutantes pour tout aspirant à la science des données au départ.. Étant donné que les deux sont extrêmement importants pour évaluer les problèmes de régression, nous les comprendrons et les comparerons en profondeur. Les deux ont leurs avantages et leurs inconvénients, dont nous discuterons en détail dans cet article.
Noter: Pour comprendre R-carré et R-carré ajusté, doit avoir une bonne connaissance de la régression linéaire. Consultez notre cours gratuit –
Table des matières
- Somme résiduelle des carrés
- Comprendre la statistique R-carré
- Problèmes avec la statistique R-carré
- Statistiques R carrées ajustées
Somme résiduelle des carrés
Comprendre clairement les concepts, nous aborderons un problème de régression simple. Ici, estamos tratando de predecir las ‘calificaciones obtenidas’ en función de la cantidad de ‘tiempo dedicado a estudiar’. Les conditions météorologiques passé à étudier sera notre variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... Indépendant et le marques de commerce accompli dans le test est notre dépendant O variable cible.
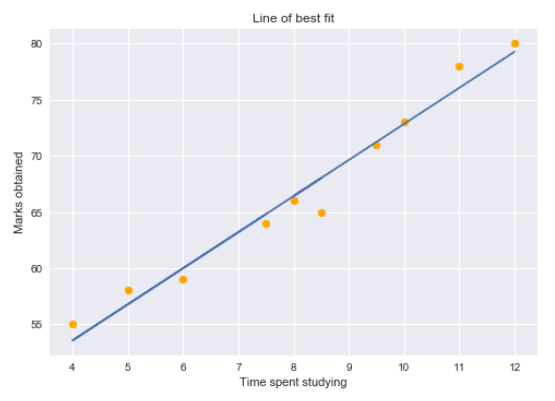
Nous pouvons tracer un graphique de régression simple pour visualiser ces données.
Les points jaunes représentent les points de données et la ligne bleue est notre ligne de régression prédite. Comme tu peux le voir, notre modèle de régression ne prédit pas parfaitement tous les points de données. Ensuite, Comment évaluons-nous les prédictions de ligne de régression à l’aide des données?? Bon, nous pourrions commencer par déterminer les valeurs résiduelles pour les points de données.
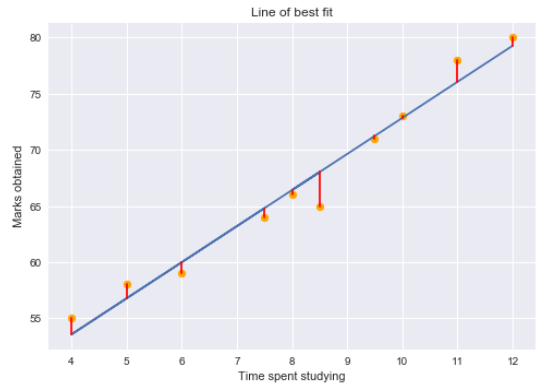
Résiduel pour un point dans les données est la différence entre la valeur réelle et la valeur prédite par notre modèle de régression linéaire.
Les graphiques de résidus nous indiquent si le modèle de régression convient ou non aux données. En réalité, est une hypothèse du modèle de régression selon laquelle il n’y a pas de tendance dans les graphiques de résidus. Étudier en détail les hypothèses de régression linéaire, Je suggère de passer par ce grand arlacculum!
Utilisation de valeurs résiduelles, nous pouvons déterminer la somme des carrés des déchets également connus sous le nom de Somme résiduelle des carrés ou RSS.
Plus la valeur RSS est faible, meilleures sont les prédictions du modèle. Ou nous pouvons dire qu’une ligne de régression est une ligne mieux ajustée si elle minimise la valeur RSS.. Mais il y a un défaut là-dedans.: RSS est une statistique de variante d’échelle. Puisque RSS est la somme de la différence au carré entre la valeur réelle et la valeur prédite, la valeur dépend de l’échelle de la variable cible.
Exemple:
Considérez que votre variable cible est le revenu généré par la vente d’un produit. Les déchets dépendraient de l’ampleur de cet objectif. Si l’échelle de revenu est prise en compte « Des centaines de roupies » (c'est-à-dire, l’objectif serait 1, 2, 3, etc.), alors nous pourrions obtenir un RSS d’environ 0,54 (parlant hypothétiquement).
Mais si la variable cible du revenu a été prise en compte « roupies » (c'est-à-dire, l’objectif serait 100, 200, 300, etc.), alors nous pourrions obtenir un RSS plus élevé comme 5400. Bien que les données ne changent pas, La valeur RSS varie. selon l’ampleur de l’objectif. Il est donc difficile de juger de ce que pourrait être une bonne valeur RSS..
Ensuite, Pouvons-nous trouver une meilleure statistique qui soit invariante en échelle?? C’est là que R-carré entre en scène.
Comprendre les statistiques R-carré
La statistique R-carré ou coefficient de détermination est une statistique invariante d’échelle qui fournit la proportion de variation dans la variable cible expliquée par le modèle de régression linéaire.
Cela peut sembler un peu compliqué., alors laissez-moi le décomposer ici. Déterminer la proportion de variation cible expliquée par le modèle, tout d’abord, nous devons déterminer ce qui suit:
-
Somme totale des carrés
La variation totale de la variable cible est la somme des carrés de la différence entre les valeurs réelles et leur moyenne.
TSS ou somme totale des carrés donne la variation totale en Y. Nous pouvons voir qu’elle est très similaire à la variance de Y. Alors que la variance est la moyenne des sommes carrées de la différence entre les valeurs réelles et les points de données, TSS est le total des sommes au carré.
Maintenant que nous connaissons la variation totale de la variable cible, Comment déterminer la proportion de cette variation expliquée par notre modèle ?? Retour à RSS.
-
Somme résiduelle des carrés
Comme nous en avons discuté précédemment, RSS nous donne le carré total de la distance des points réels de la droite de régression. Mais si nous nous concentrons sur un seul déchet, on peut dire que c’est la distance qui n’est pas captée par la droite de régression. Donc, RSS dans son ensemble nous donne la variation de la variable cible qui est non expliqué par notre modèle.
-
Calculer R-carré
À présent, si TSS nous donne la variation totale de Y, et RSS nous donne la variation de Y non expliquée par X, ensuite TSS-RSS nous donne la variation de Y qui est expliquée par notre modèle! On peut simplement diviser cette valeur par TSS pour obtenir le rapport de variation en Y qui explique le modèle. Et c’est le nôtre Statistique r-carré!
R-carré = (TSS-RSS) / TSS
= Variation expliquée / Variation totale
= 1 – Variation inexpliquée / Variation totale
Ensuite, Square R donne le degré de variabilité de la variable cible qui est expliqué par le modèle ou les variables indépendantes. Si cette valeur est 0,7, signifie que les variables indépendantes expliquent le 70% de la variation de la variable cible.
La valeur de R carré est toujours comprise entre 0 Oui 1. Une valeur R-carré plus élevée indique une plus grande quantité de variabilité expliquée par notre modèle et vice versa.
Si nous avions une valeur RSS vraiment faible, signifierait que la droite de régression était très proche des points réels. Cela signifie que des variables indépendantes expliquent la majeure partie de la variation de la variable cible.. Dans ce cas, nous aurions une valeur R carrée très élevée.
Au contraire, si nous avions une valeur RSS très élevée, cela signifierait que la ligne de régression serait très éloignée des points réels. Donc, les variables indépendantes ne parviennent pas à expliquer la majeure partie de la variation de la variable cible. Cela nous donnerait une valeur R-carré vraiment faible..
Ensuite, cela explique pourquoi la valeur R-carré nous donne la variation de la variable cible donnée par la variation des variables indépendantes.
Problèmes avec la statistique R-carré
La statistique R-carré n’est pas parfaite. En réalité, souffre d’un défaut majeur. Sa valeur ne diminue jamais, peu importe le nombre de variables que nous ajoutons à notre modèle de régression.. C'est-à-dire, même si nous ajoutons des variables redondantes aux données, la valeur de R carré ne diminue pas. Soit il reste le même, soit il augmente avec l’ajout de nouvelles variables indépendantes. Cela n’a clairement pas de sens car certaines des variables indépendantes peuvent ne pas être utiles pour déterminer la variable cible.. Le R-carré ajusté traite de ce problème.
Statistiques R carrées ajustées
Le R-carré ajusté prend en compte le nombre de variables indépendantes utilisées pour prédire la variable cible. Ce faisant, nous pouvons déterminer si l’ajout de nouvelles variables au modèle augmente réellement l’ajustement du modèle.
Jetons un coup d’œil à la formule R-carré ajustée pour mieux comprendre son fonctionnement.
Ici,
- Nord représente le nombre de points de données dans notre jeu de données
- k représente le nombre de variables indépendantes, Oui
- R représente les valeurs R-carré déterminées par le modèle.
Ensuite, si R-carré n’augmente pas significativement avec l’ajout d’une nouvelle variable indépendante, alors la valeur R-carré ajustée diminuera réellement.
D'un autre côté, si lors de l’ajout de la nouvelle variable indépendante, nous constatons une augmentation significative de la valeur de R au carré, alors la valeur du carré R ajusté augmentera également.
Nous pouvons voir la différence entre les valeurs de R carré et R carré ajusté si nous ajoutons une variable indépendante aléatoire à notre modèle.
Comme tu peux le voir, l’ajout d’une variable indépendante aléatoire n’a pas aidé à expliquer la variation de la variable cible. Notre valeur R-carré reste la même. Donc, nous donne une fausse indication que cette variable pourrait être utile pour prédire la sortie. Cependant, la valeur R-carré ajustée a diminué, qui indiquait que cette nouvelle variable ne saisissait pas réellement la tendance dans la variable cible.
Clairement, il est préférable d’utiliser le R-carré ajusté lorsqu’il y a plusieurs variables dans le modèle de régression. Cela nous permettrait de comparer des modèles avec différents nombres de variables indépendantes..
Remarques finales
Dans cet article, nous analysons ce qu’est la statistique R-carré et où elle échoue. Nous examinons également le carré R ajusté.
Avec chance, cela vous a donné une meilleure compréhension des choses. Vous pouvez maintenant déterminer avec prudence quelles variables indépendantes sont utiles pour prédire le résultat de votre problème de régression..
Pour en savoir plus sur d’autres mesures d’évaluation, Je suggère de consulter les excellentes ressources suivantes: