Noter: Cet article a été initialement publié le 10 octobre 2014 et le 27 Mars 2018.
Vue d'ensemble
- Comprendre le voisin le plus proche (KNN): l'un des algorithmes d'apprentissage automatique les plus populaires
- Découvrez comment fonctionne kNN en python
- Choisissez la bonne valeur de k en termes simples
introduction
Au cours des quatre années de ma carrière en science des données, j'ai construit plus de 80% de modèles de classification et un seul 15-20% modèles de régression. Ces ratios peuvent être plus ou moins généralisés à l'ensemble de l'industrie. La raison de ce biais envers modèles de classification est que la plupart des problèmes analytiques impliquent de prendre une décision.
Par exemple, si un client s'usera ou non, si on va chez le client X pour les campagnes digitales, si le client a un potentiel élevé ou non, etc. Ces analyses sont plus perspicaces et sont directement liées à une feuille de route de mise en œuvre.
Dans cet article, nous parlerons d'un autre apprentissage automatique largement utilisé. technique de classementmoi appelés voisins les plus proches K (KNN). Nous nous concentrerons principalement sur le fonctionnement de l'algorithme et la manière dont le paramètre d'entrée affecte la sortie. / prédiction.
Noter: Les personnes qui préfèrent apprendre à travers des vidéos peuvent apprendre la même chose grâce à notre cours gratuit – Algorithme des voisins les plus proches (KNN) en Python et R. Et si vous êtes un débutant absolu en science des données et en apprentissage automatique, consultez notre programme BlackBelt certifié:
Table des matières
- Quand utilisons-nous l'algorithme KNN?
- Comment fonctionne l'algorithme KNN?
- Comment choisissons-nous le facteur K?
- Le briser – Pseudo-code KNN
- Implémentation Python à partir de zéro
- Comparer notre modèle avec scikit-learn
Quand utilisons-nous l'algorithme KNN?
KNN peut être utilisé pour des problèmes de classification prédictive et de régression. Cependant, le plus largement utilisé dans les problèmes de classification dans l'industrie. Pour évaluer toute technique, nous regardons habituellement 3 aspects importants:
1. Facilité d'interprétation de la sortie
2. Temps de calcul
3. Puissance prédictive
Prenons quelques exemples pour placer KNN sur l'échelle:
Ferias de algoritmos KNN a través de todos los paramètresLes "paramètres" sont des variables ou des critères qui sont utilisés pour définir, mesurer ou évaluer un phénomène ou un système. Dans divers domaines tels que les statistiques, Informatique et recherche scientifique, Les paramètres sont essentiels à l’établissement de normes et de standards qui guident l’analyse et l’interprétation des données. Leur sélection et leur manipulation correctes sont cruciales pour obtenir des résultats précis et pertinents dans toute étude ou projet.... de consideraciones. Il est couramment utilisé pour sa facilité d'interprétation et son faible temps de calcul.
Comment fonctionne l'algorithme KNN?
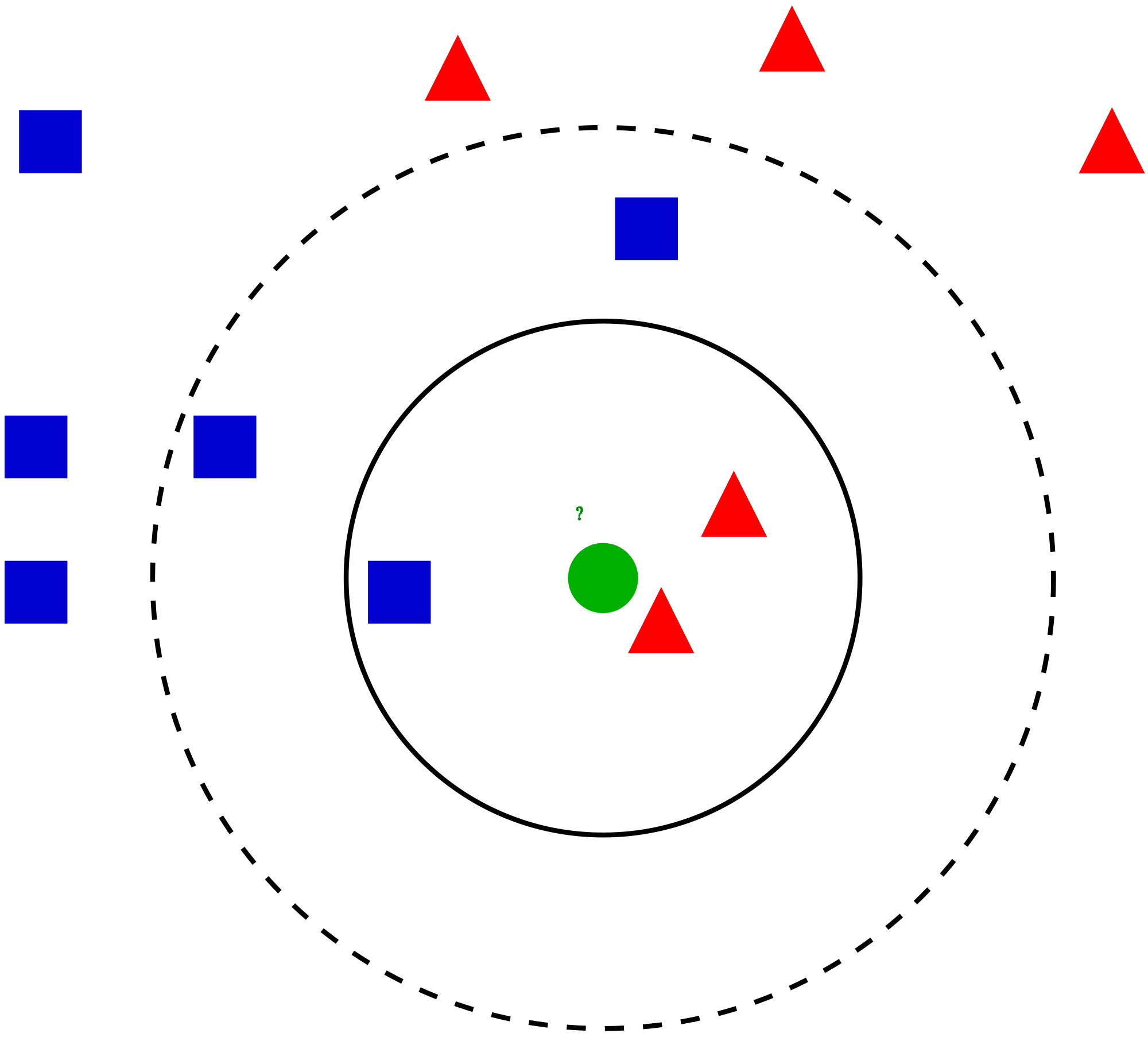
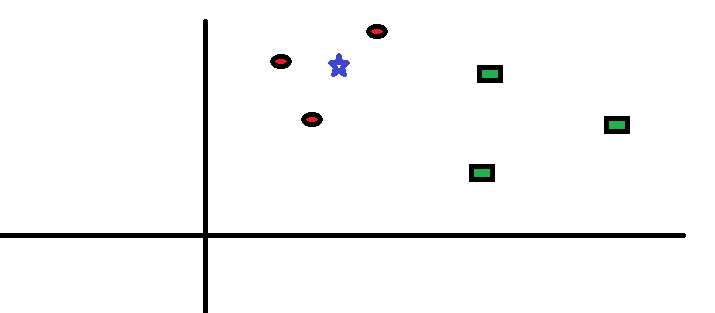
Prenons un cas simple pour comprendre cet algorithme. Ci-dessous, une extension de cercles rouges (RC) et carrés verts (SG):
Il a l'intention de découvrir la classe de l'étoile bleue (BS). BS peut être RC ou GS et rien d'autre. L'algorithme “K” fr KNN est le voisin le plus proche pour lequel nous voulons voter. Disons que K = 3. Donc, maintenant nous allons faire un cercle avec BS comme centre si grand qu'il n'enferme que trois points de données dans le plan. Veuillez vous référer au schéma suivant pour plus de détails:
Les trois points les plus proches de BS sont tous RC. Pourtant, avec un bon niveau de confiance, on peut dire que le BS devrait appartenir à la classe RC. Ici, le choix est devenu très évident car les trois votes des voisins les plus proches sont allés à RC. Le choix du paramètre K est très important dans cet algorithme. Ensuite, nous comprendrons quels sont les facteurs à considérer pour conclure le meilleur K.
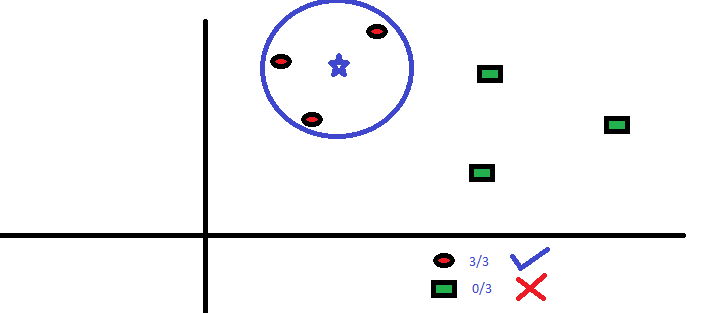
Comment choisissons-nous le facteur K?
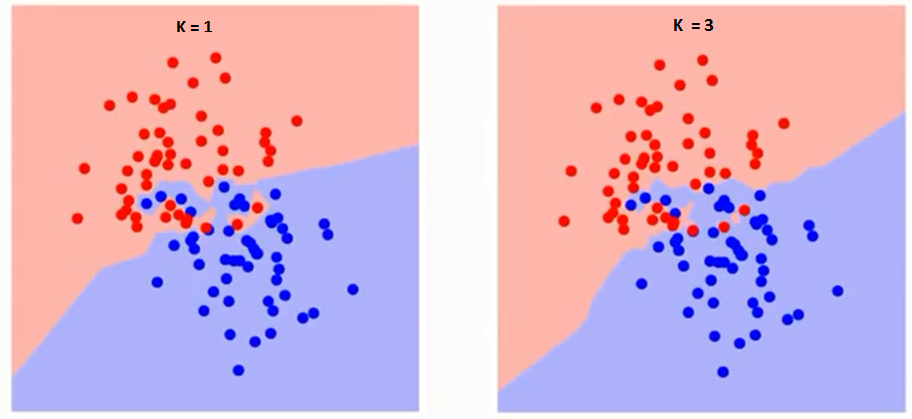
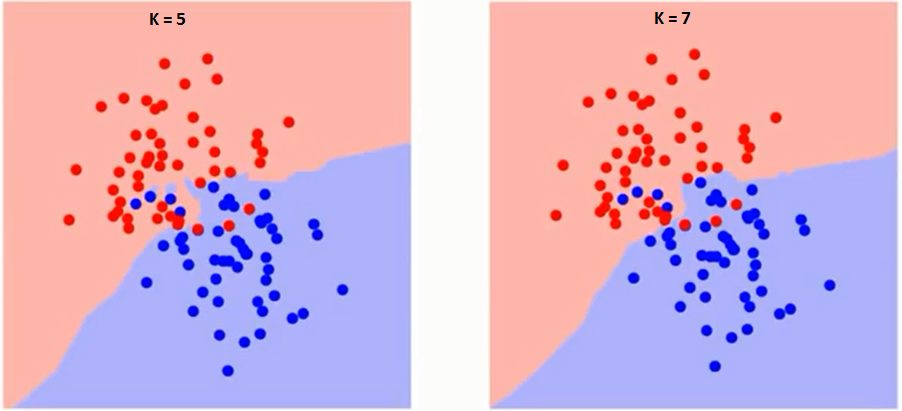
Essayons d'abord de comprendre ce qui exactement K influence l'algorithme. Si nous voyons le dernier exemple, depuis le 6 observaciones de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines.... permanecen constantes, avec une valeur K donnée, nous pouvons définir des limites pour chaque classe. Ces limites sépareront RC de GS. De la même manière, essayons de voir l'effet de la valeur “K” dans les limites de la classe. Voici les différentes limites qui séparent les deux classes avec des valeurs différentes de K.
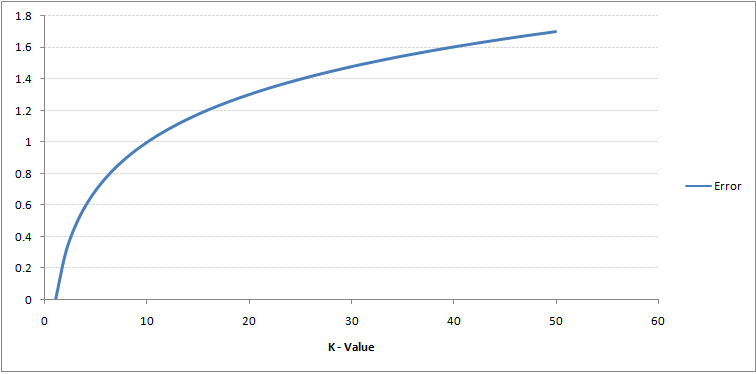
Si tu regardes de près, vous pouvez voir que la limite devient plus lisse à mesure que la valeur de K augmente. Avec K croissant à l'infini, il devient enfin tout bleu ou tout rouge, selon la majorité totale. Le taux d'erreur d'entraînement et le taux d'erreur de validation sont deux paramètres dont nous avons besoin pour accéder à différentes valeurs K.. A continuación se muestra la curva para la tasa de error de entrenamiento con un valor variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... de K:
Comme tu peux le voir, le taux d'erreur en K = 1 est toujours égal à zéro pour l'échantillon d'apprentissage. En effet, le point le plus proche de tout point de données d'entraînement est lui-même, donc la prédiction est toujours exacte avec K = 1. Si la courbe d'erreur de validation avait été similaire, notre choix de K aurait été 1. Ci-dessous la courbe d'erreur de validation avec une valeur variable de K:
Cela clarifie l'histoire. Et K = 1, nous dépassions les limites. Pourtant, le taux d'erreur diminue initialement et atteint un minimum. Après le point minimum, augmente avec l'augmentation de K. Pour obtenir la valeur optimale de K, peut séparer la formation et la validation initiale de l'ensemble de données. Tracez maintenant la courbe d'erreur de validation pour obtenir la valeur optimale de K. Cette valeur de K doit être utilisée pour toutes les prédictions.
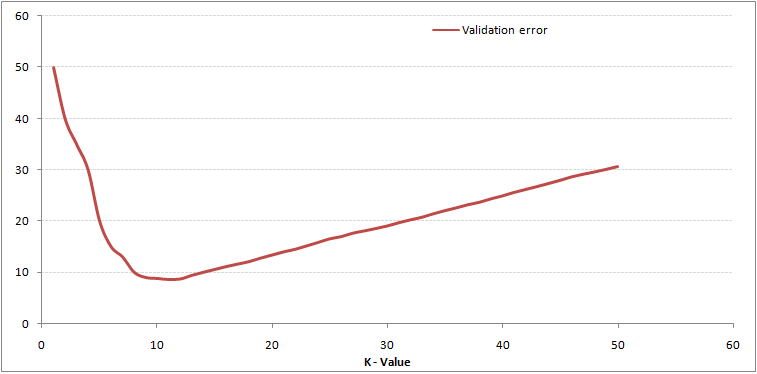
Le contenu ci-dessus peut être compris de manière plus intuitive en utilisant notre cours gratuit: Algorithme des voisins les plus proches (KNN) en Python et R
Le briser – Pseudo-code KNN
Nous pouvons implémenter un modèle KNN en suivant les étapes ci-dessous:
- Charger les données
- Initialiser la valeur de k
- Pour obtenir la classe prédite, répéter de 1 jusqu'au nombre total de points de données d'entraînement
- Calculer la distance entre les données de test et chaque ligne de données d'entraînement. Ici, nous utiliserons la distance euclidienne comme métrique de distance, car c'est la méthode la plus populaire. Les autres métriques qui peuvent être utilisées sont Chebyshev, cosinus, etc.
- Trier les distances calculées par ordre croissant en fonction des valeurs de distance
- Obtenir les k premières lignes de la matrice ordonnée
- Obtenez la classe la plus fréquente à partir de ces lignes
- Renvoie la classe prédite
Implémentation Python à partir de zéro
Nous utiliserons le jeu de données Iris populaire pour construire notre modèle KNN. Vous pouvez le télécharger depuis ici.
Comparer notre modèle avec scikit-learn
de sklearn.neighbors importer KNeighborsClassifier hennissement = KNeighborsClassifier(n_voisins=3) neigh.fit(data.iloc[:,0:4], Les données['Nom']) # Classe prévue imprimer(hennir.prédire(test)) -> ['Iris-virginica'] # 3 voisins les plus proches imprimer(voisins.genoux(test)[1]) -> [[141 139 120]]
Nous pouvons voir que les deux modèles ont prédit la même classe (« Iris virginica ») et les mêmes voisins les plus proches ( [141 139 120] ). Donc, nous pouvons conclure que notre modèle fonctionne comme prévu.
Implémentation de kNN dans R
Paso 1: importer les données
Paso 2: vérifier les données et calculer le résumé des données
Production
#Principales observations présentes dans les données SepalLength SepalWidth PetalLength PetalWidth Name 1 5.1 3.5 1.4 0.2 Iris-soyeux 2 4.9 3.0 1.4 0.2 Iris-soyeux 3 4.7 3.2 1.3 0.2 Iris-soyeux 4 4.6 3.1 1.5 0.2 Iris-soyeux 5 5.0 3.6 1.4 0.2 Iris-soyeux 6 5.4 3.9 1.7 0.4 Iris-setosa #Vérifier les dimensions des données [1] 150 5 #Résumer les données SepalLength SepalWidth PetalLength PetalWidth Name Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 Iris-soyeux :50 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 Iris-versicolor:50 Médian :5.800 Médian :3.000 Médian :4.350 Médian :1.300 Iris-virginica :50 Moyenne :5.843 Moyenne :3.054 Moyenne :3.759 Moyenne :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Paso 3: diviser les données
Paso 4: Calculer la distance euclidienne
Paso 5: écrire la fonction pour prédire kNN
Paso 6: Calcul de l'étiquette (nom) pour K = 1
Production
Pour K=1 [1] "Iris-virginica"
De la même manière, peut calculer d'autres valeurs de K.
Comparaison de notre fonction de prédiction kNN avec la bibliothèque “Classe”
Production
Pour K=1 [1] "Iris-virginica"
Nous pouvons voir que les deux modèles ont prédit la même classe (« Iris virginica »).
Remarques finales
L'algorithme KNN est l'un des algorithmes de classification les plus simples. Même avec une telle simplicité, peut donner des résultats très compétitifs. L'algorithme KNN peut également être utilisé pour des problèmes de régression. La seule différence avec la méthodologie discutée sera l'utilisation des moyennes des plus proches voisins au lieu de voter pour les plus proches voisins.. KNN peut être encodé sur une seule ligne en R. Je n'ai pas encore exploré comment nous pouvons utiliser l'algorithme KNN dans SAS.
L'article vous a-t-il été utile? Avez-vous utilisé d'autres outils d'apprentissage automatique récemment? Envisagez-vous d'utiliser KNN dans l'un de vos problèmes commerciaux? Si c'est ainsi, dites nous comment vous comptez le faire.
