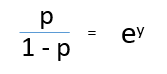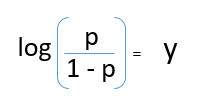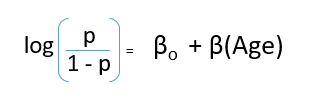Régression logistique R | Introduction à la régression logistique

Vue d'ensemble

• Obtenez une introduction à la régression logistique en utilisant R et Python
• La régression logistique est un algorithme de classification populaire utilisé pour prédire un résultat binaire
• Il existe plusieurs métriques pour évaluer un modèle de régression logistique, comme matrice de confusion, Courbe AUC-ROC, etc.

introduction

Tous algorithme d'apprentissage automatique fonctionne mieux dans un ensemble donné de conditions. Assurez-vous que votre algorithme correspond aux hypothèses / exigences garantit des performances supérieures. Aucun algorithme ne peut être utilisé dans n'importe quelle condition. Par exemple: Avez-vous déjà essayé d'utiliser régression linéaire dans une variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... dependiente categórica? N'essaye même pas! Parce que vous ne serez pas apprécié pour obtenir des valeurs extrêmement basses de la stat R² et F ajustée.

En échange, dans de telles situations, vous devriez essayer d'utiliser des algorithmes comme la régression logistique, Arbres de décision, SVM, Forêt aléatoire, etc. Pour un aperçu rapide de ces algorithmes, je recommanderai la lecture: Concepts de base des algorithmes d'apprentissage automatique.

avec ce poste, je vous apporte des connaissances utiles sur la régression logistique dans R. Une fois que vous avez maîtrisé la régression linéaire, c'est la prochaine étape naturelle de votre voyage. Il est également facile à apprendre et à mettre en œuvre, mais vous devriez connaître la science derrière cet algorithme.

J'ai essayé d'expliquer ces concepts de la manière la plus simple possible. Commençons.

Qu'est-ce que la régression logistique?

La régression logistique en est une algorithme de classification. Il est utilisé pour prédire un résultat binaire (1/0, Oui / Non, Vrai / Faux) étant donné un ensemble de variables indépendantes. Représenter un résultat binaire / catégorique, nous utilisons des variables muettes. Vous pouvez également considérer la régression logistique comme un cas particulier de régression linéaire lorsque la variable de résultat est catégorielle, où nous utilisons le log des cotes comme variable dépendante. En mots simples, prédire la probabilité d'occurrence d'un événement en ajustant les données à une fonction logit.

Dérivation de l'équation de régression logistique

La régression logistique fait partie d'une classe plus large d'algorithmes connue sous le nom de modèle linéaire généralisé. (glm). Dans 1972, Nelder et Wedderburn ont proposé ce modèle dans le but de fournir un moyen d'utiliser la régression linéaire pour des problèmes qui n'étaient pas directement adaptés à l'application de la régression linéaire.. En réalité, a proposé une classe de différents modèles (régression linéaire, ANOVA, Régression de Poisson, etc.) qui incluait la régression logistique comme cas particulier.

L'équation fondamentale du modèle linéaire généralisé est:

g(E(Oui)) = α + βx1 + γx2

Ici, g () est la fonction de lien, E (Oui) est l'espérance de la variable cible et α + βx1 + γx2 est le prédicteur linéaire (une, b, γ prédire). Le rôle de la fonction de lien est “lien” l'espérance de y au prédicteur linéaire.

Points importants

1. GLM ne suppose pas une relation linéaire entre les variables dépendantes et indépendantes. Cependant, suppose une relation linéaire entre la fonction de lien et les variables indépendantes dans le modèle logit.
2. La variable dépendante n'a pas besoin d'être distribuée normalement..
3. Ne pas utiliser OLS (Moindres carrés ordinaires) para la estimación de paramètresLes "paramètres" sont des variables ou des critères qui sont utilisés pour définir, mesurer ou évaluer un phénomène ou un système. Dans divers domaines tels que les statistiques, Informatique et recherche scientifique, Les paramètres sont essentiels à l’établissement de normes et de standards qui guident l’analyse et l’interprétation des données. Leur sélection et leur manipulation correctes sont cruciales pour obtenir des résultats précis et pertinents dans toute étude ou projet..... En échange, utilise l'estimation du maximum de vraisemblance (MLE).
4. Les erreurs doivent être indépendantes mais non distribuées normalement..

Comprenons plus avec un exemple:

Nous disposons d'un échantillon de 1000 les clients. Nous devons prédire la probabilité qu'un client achète (Oui) un magazine particulier ou non. Comme tu peux le voir, nous avons une variable de résultat catégoriel, nous utiliserons la régression logistique.

Pour commencer avec la régression logistique, Je vais d'abord écrire l'équation de régression linéaire simple avec la variable dépendante enfermée dans une fonction de lien:

                           g(Oui) = βo + b(Âge)         ---- (une)

Noter: Pour faciliter la compréhension, J'ai considéré 'Âge’ comme variable indépendante.

Dans la régression logistique, nous nous intéressons uniquement à la probabilité de la variable dépendante du résultat (succès ou échec). Comme décrit ci-dessus, g () est la fonction de lien. Cette fonction est définie par deux choses: probabilité de succès (p) et probabilité d'échec (1-p). p doit répondre aux critères suivants:

1. devrait toujours être positif (depuis p> = 0)
2. Doit toujours être inférieur à égal à 1 (depuis p <= 1)

À présent, nous allons simplement satisfaire ces 2 conditions et nous arriverons au cœur de la régression logistique. Pour définir la fonction de lien, nous noterons g () avec 'p’ initialement et finalement nous finirons par dériver cette fonction.

Comme la probabilité doit toujours être positive, on va mettre l'équation linéaire sous forme exponentielle. Pour toute valeur de pente et de variable dépendante, l'exposant de cette équation ne sera jamais négatif.

p = exp(βo + b(Âge)) = e^(βo + b(Âge))    ------- (b)

Pour que la probabilité soit inférieure à 1, il faut diviser p par un nombre supérieur à p. Cela peut se faire simplement en:

p = exp(βo + b(Âge)) / exp(βo + b(Âge)) + 1   = e^(βo + b(Âge)) / e ^(βo + b(Âge)) + 1    ----- (c)

En utilisant (une), (b) Oui (c), nous pouvons redéfinir la probabilité comme:

              p = e^y/ 1 + e ^ y           --- (ré)

où p est la probabilité de succès. Ce (ré) est la fonction logit

Si p est la probabilité de succès, 1-p sera la probabilité de défaillance qui peut s'écrire:

q = 1 - p = 1 - (e^y/ 1 + e ^ y)    --- (e)

où quelle est la probabilité d'échec

lors de la division, (ré) / (e), on obtient,

Après avoir pris la bûche des deux côtés, on obtient,

Journal (p / 1-p) est la fonction de lien. La transformation logarithmique de la variable de résultat nous permet de modéliser une association non linéaire de manière linéaire.

Après avoir remplacé la valeur de y, Nous obtiendrons:

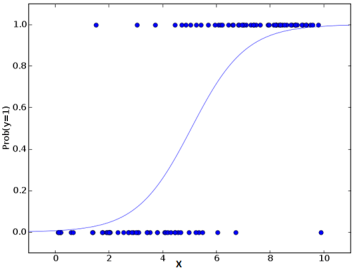
C'est l'équation utilisée dans la régression logistique. Ici (p / 1-p) est le rapport impair. Lorsque le logarithme du rapport impair est déterminé comme étant positif, la probabilité de succès est toujours supérieure à 50%. Vous trouverez ci-dessous un tracé de modèle logistique typique. Vous pouvez voir que la probabilité ne descend jamais en dessous 0 et ci-dessus 1.

Performances du modèle de régression logistique

Évaluer les performances d'un modèle de régression logistique, nous devons considérer certaines métriques. Quel que soit l'outil (SAS, R, Python) dans lequel je travaillerais, cherche toujours:

1. AIC (Critères d'information d'Akaike) – La métrique analogue du R2 ajusté dans la régression logistique est l'AIC. AIC est la mesure d'ajustement qui pénalise le modèle par le nombre de coefficients dans le modèle. Donc, nous préférons toujours le modèle avec une valeur AIC minimale.

2. Écart nul et écart résiduel – La déviance nulle indique la réponse prédite par un modèle avec rien de plus qu'une interception. Baisser la valeur, mieux le modèle. La déviance résiduelle indique la réponse prédite par un modèle lors de l'ajout de variables indépendantes. Baisser la valeur, mieux le modèle.

3. Matrice de confusion: Ce n'est rien de plus qu'une représentation tabulaire des valeurs réelles par rapport aux valeurs prédites. Cela nous aide à trouver la précision du modèle et à éviter le surajustement.. Voici à quoi cela ressemble:

La source: (prise – m – But)

Vous pouvez calculer le précision de votre modèle avec:

De la matrice de confusion, la spécificité et la sensibilité peuvent être dérivées comme illustré ci-dessous:

La spécificité et la sensibilité jouent un rôle crucial dans la dérivation de la courbe ROC..

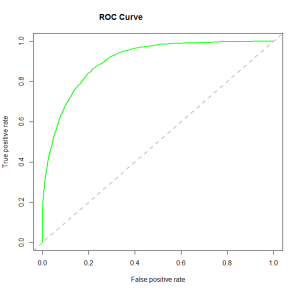
4. courbe ROC: La caractéristique de fonctionnement du récepteur (ROC) résume les performances du modèle en évaluant les compromis entre le taux de vrais positifs (sensibilité) et le taux de faux positifs (1 spécificité). Pour tracer le ROC, il est conseillé de supposer p> 0.5 puisque nous sommes plus préoccupés par le taux de réussite. ROC résume le pouvoir prédictif pour toutes les valeurs possibles de p> 0.5. L'aire sous la courbe (ASC), denominada indiceLe "Indice" C’est un outil fondamental dans les livres et les documents, qui vous permet de localiser rapidement les informations souhaitées. Généralement, Il est présenté au début d’une œuvre et organise les contenus de manière hiérarchique, y compris les chapitres et les sections. Sa préparation correcte facilite la navigation et améliore la compréhension du matériau, ce qui en fait une ressource incontournable tant pour les étudiants que pour les professionnels dans divers domaines.... précision (UNE) l'indice de concordance, est une mesure de performance parfaite pour la courbe ROC. Plus l'aire sous la courbe est grande, meilleur est le pouvoir prédictif du modèle. Ci-dessous un exemple de courbe ROC. Le ROC d'un modèle prédictif parfait a TP égal à 1 et FP égal à 0. Cette courbe touchera le coin supérieur gauche du graphique.

Noter: Pour les performances du modèle, vous pouvez également considérer la fonction de probabilité. On l'appelle ainsi car il sélectionne les valeurs des coefficients qui maximisent la probabilité d'expliquer les données observées.. Indique la qualité de l'ajustement lorsque sa valeur est proche de un et un mauvais ajustement des données lorsque sa valeur est proche de zéro..

Modèle de régression logistique en R et Python

Le code R est fourni ci-dessous, mais si vous êtes un utilisateur de python, voici une fenêtre de code étonnante pour construire votre modèle de régression logistique. Pas besoin d'ouvrir Jupyter, puede hacerlo todo aquí:

Teniendo en cuenta la disponibilidad, construí este modelo en nuestro problema de práctica: el conjunto de datos de Dressify. Puedes descargarlo ici.

Sin profundizar en la ingeniería de características, aquí está el script del modelo de regresión logística simple:

ensemble('C:/Utilisateurs/manish/Desktop/dressdata')

#load data
train <- lire.csv(« Train_Old.csv »)

#create training and validation data from given data
install.packages('caTools')
une bibliothèque(caOutils)

set.seed(88)
diviser <- échantillon.split(train$Recommandé, SplitRatio = 0.75)

#get training and test data
dresstrain <- sous-ensemble(former, split == VRAI)
dresstest <- sous-ensemble(former, split == FAUX)

#logistic regression model
model <- glm (Recommandé ~ .-ID, données = dresstrain, famille = binôme)
sommaire(maquette)

prédire <- prédire(maquette, tapez="réponse")

#confusion matrix
table(dresstrain$Recommandé, prédire > 0.5)

#ROCR Curve
library(Le ROCR)
ROCRpred <- prédiction(prédire, dresstrain$Recommandé)
ROCRperf <- performance(ROCRpred, 'tpr','fpr')
terrain(ROCRperf, colorize = VRAI, text.adj = c(-0.2,1.7))

#plot glm
library(ggplot2)
ggplot(dresstrain, aes(x=Évaluation, y=Recommandé)) + geom_point() + 
stat_smooth(méthode="glm", famille ="binôme", se=FAUX)

Ces données nécessitent beaucoup de nettoyage et d'ingénierie de fonctionnalités. La portée de cet article m'a limité à garder l'exemple concentré sur la construction du modèle de régression logistique.. Ces données sont disponible pour pratiquer. Je vous recommande de travailler sur ce problème. Il y a trop à apprendre.

Remarques finales

À ce point, vous connaissez déjà la science derrière la régression logistique. J'ai vu à plusieurs reprises que les gens connaissent l'utilisation de cet algorithme sans avoir connaissance de ses concepts de base. J'ai fait de mon mieux pour expliquer cette partie aussi simplement que possible. L'exemple ci-dessus montre simplement le squelette de l'utilisation de la régression logistique dans R. Avant d'aborder vraiment cette étape, vous devriez consacrer votre temps crucial à l'ingénierie des fonctionnalités.

En outre, Je vous recommande de travailler sur cet ensemble de problèmes. Vous exploreriez des choses auxquelles vous n'auriez peut-être pas été confrontées auparavant.

Ai-je raté quelque chose d'important? Trouvez-vous utile cet article? Partagez vos opinions / pensées dans la section des commentaires ci-dessous.

Si vous aimez ce que vous venez de lire et souhaitez continuer à apprendre sur l'analyse, abonnez-vous à nos e-mails, Suivez-nous sur Twitter ou comme le nôtre page le Facebook.

En rapport