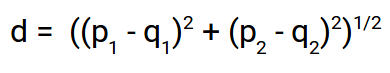Ce message a été rendu public dans le cadre de la Blogathon sur la science des données.
introduction
Avez-vous déjà rêvé de créer votre propre application de similarité d'images ?, pero tiene miedo de no saber lo suficiente sobre l'apprentissage en profondeurL'apprentissage en profondeur, Une sous-discipline de l’intelligence artificielle, s’appuie sur des réseaux de neurones artificiels pour analyser et traiter de grands volumes de données. Cette technique permet aux machines d’apprendre des motifs et d’effectuer des tâches complexes, comme la reconnaissance vocale et la vision par ordinateur. Sa capacité à s’améliorer continuellement au fur et à mesure que de nouvelles données lui sont fournies en fait un outil clé dans diverses industries, de la santé..., convolucional neuronal rougeRéseaux de neurones convolutifs (CNN) sont un type d’architecture de réseau neuronal conçu spécialement pour le traitement de données avec une structure en grille, comme images. Ils utilisent des couches de convolution pour extraire des caractéristiques hiérarchiques, Ce qui les rend particulièrement efficaces dans les tâches de reconnaissance et de classification des formes. Grâce à sa capacité à apprendre à partir de grands volumes de données, Les CNN ont révolutionné des domaines tels que la vision par ordinateur.. et de plus? Évitez de vous inquiéter. Le didacticiel suivant vous aidera à démarrer et à coder votre propre application de similarité d'images avec des mathématiques de base.
Avant de passer aux maths et au code, je te poserais une question simple. Étant donné deux images de référence et une image de test, À laquelle pensez-vous que notre image de test appartient à deux ??
Image de référence 1
Image de référence 2
Tester l'image
Si vous pensez que notre image de test est similaire à notre première image de référence, Tu as raison. Si vous croyez le contraire, Découvrons avec la puissance des mathématiques et de la programmation.
« L'avenir de la recherche se concentrera sur les images plutôt que sur les mots-clés ». – Ben Silbermann, PDG de Pinterest.
Image vectorielle
Chaque image est stockée dans notre ordinateur sous forme de nombres et un vecteur de tels nombres qui peut décrire pleinement notre image est connu sous le nom de vecteur d'image..
Distance euclidienne:
La distance euclidienne représente la distance entre deux points quelconques dans un espace à n dimensions. Puisque nous représentons nos images comme des vecteurs d'images, ils ne sont rien de plus qu'un point dans un espace de n dimensions et nous allons utiliser la distance euclidienne pour trouver la distance entre eux.
Histogramme:
Un histogramme est un affichage graphique de valeurs numériques. Nous utiliserons le vecteur image pour les trois images puis nous trouverons la distance euclidienne entre elles. Sur la base des valeurs renvoyées, l'image avec une distance plus petite est plus similaire que l'autre.
Pour trouver la similitude entre les deux images, nous utiliserons l'approche suivante:
- Lire les fichiers image sous forme de tableau.
- Étant donné que les fichiers image sont colorés, il y a 3 canaux pour les valeurs RVB. Nous allons les aplatir pour que chaque image soit une seule matrice 1-D.
- Une fois que nous avons nos fichiers image sous forme de tableau, nous allons générer un histogramme pour chaque image où pour chaque index 0-255 comptons l'occurrence de cette valeur de pixel dans l'image.
- Une fois que nous avons nos histogrammes, nous utiliserons la règle L2 ou la distance euclidienne pour trouver la différence entre les deux histogrammes.
- Basé sur la distance entre l'histogramme de notre image de test et les images de référence, nous pouvons trouver l’image à laquelle notre image de test est la plus similaire..
Codage pour la similitude d’image en Python
Importer les dépendances que nous allons utiliser
from PIL import Image
from collections import Counter
import numpy as np
Nous utiliserons NumPy pour enregistrer l’image en tant que tableau NumPy, Image pour lire l’image en termes de valeurs numériques et Compteur pour compter le nombre de fois que chaque valeur de pixel se produit (0-255) dans les images.
Lire l’image
reference_image_1 = Image.open('Reference_image1.jpg')
reference_image_arr = np.asarray(reference_image_1)
imprimer(np.forme(reference_image_arr))
>>> (250, 320, 3)
Nous pouvons voir que notre image a été correctement lue comme une matrice 3-D. A l'étape suivante, nous devons aplatir cette matrice 3-D en une matrice unidimensionnelle.
flat_array_1 = array1.flatten() imprimer(np.forme(tableau_plat_1)) >>> (245760, )
Nous allons faire les mêmes étapes pour les deux autres images. Je vais l'ignorer ici pour que vous puissiez le tester davantage.
Génération du vecteur d'histogramme de comptage:
RH1 = Compteur(tableau_plat_1)
La ligne de code suivante renvoie un dictionnaire où la clé correspond à la valeur du pixel et la valeur de la clé est le nombre de fois où ce pixel est présent dans l'image.
Une limitation de la distance euclidienne est qu'elle a besoin que tous les vecteurs soient normalisés, En d'autres termes, les deux vecteurs doivent avoir les mêmes dimensions. Pour s'assurer que notre vecteur d'histogramme est normalisé, nous allons utiliser une boucle pour de 0-255 et nous allons générer notre histogramme avec la valeur clé si la clé est présente dans l'image; cas contraire, nous ajoutons un 0.
H1 = []
pour moi à portée(256):
si je dans RH1.keys():
H1.append(D1[je])
autre:
H1.append(0)
L'extrait de code ci-dessus génère un vecteur de taille (256,) donde cada indiceLe "Indice" C’est un outil fondamental dans les livres et les documents, qui vous permet de localiser rapidement les informations souhaitées. Généralement, Il est présenté au début d’une œuvre et organise les contenus de manière hiérarchique, y compris les chapitres et les sections. Sa préparation correcte facilite la navigation et améliore la compréhension du matériau, ce qui en fait une ressource incontournable tant pour les étudiants que pour les professionnels dans divers domaines.... corresponde al valor del píxel y el valor corresponde al recuento del píxel en esa imagen.
Nous suivons les mêmes étapes pour les deux autres images et obtenons leurs Count-Histogram-Vectors correspondants. En ce point, nous avons nos vecteurs finaux pour les images de référence et l’image de test et tout ce que nous allons faire est de calculer les distances et de prédire.
Fonction de distance euclidienne:
def L2Norm(H1,H2):
distance =0
for i in range(longueur(H1)):
distance += np.carré(H1[je]-H2[je])
retourner np.sqrt(distance)
La función anterior toma dos histogrammesLes histogrammes sont des représentations graphiques qui montrent la distribution d’un ensemble de données. Ils sont construits en divisant la plage de valeurs en intervalles, O "Bacs", et compter la quantité de données tombées dans chaque intervalle. Cette visualisation vous permet d’identifier des modèles, Tendances et variabilité des données, faciliter l’analyse statistique et la prise de décision éclairée dans diverses disciplines.... y devuelve la distancia euclidiana entre ellos.
Évaluation:
Puisque nous avons tout ce dont nous avons besoin pour trouver les similitudes dans l'image, Découvrons la distance entre l'image de test et notre première image de référence.
dist_test_ref_1 = L2Norm(H1, test_H)
imprimer("La distance entre Reference_Image_1 et Test Image est : {}".format(dist_test_ref_1))
>>> La distance entre Reference_Image_1 et Test Image est : 9882.175468994668
Voyons maintenant la distance entre l'image de test et notre deuxième image de référence.
dist_test_ref_2 = L2Norm(H2,test_H)
imprimer("La distance entre Reference_Image_2 et Test Image est : {}".format(dist_test_ref_2))
>>> La distance entre Reference_Image_2 et Test Image est : 137929.0223122023
conclusion
Sur la base des résultats précédents, nous pouvons voir que la distance entre notre image de test et notre première image de référence est beaucoup plus petite que la distance entre notre test et notre deuxième image de référence, ce qui est logique car l'image de test et notre première image de référence sont des images Piegon tandis que notre deuxième image de référence est celle d'un paon.
Dans le prochain tutoriel, nous avons appris à utiliser les mathématiques de base et peu de programmation pour créer notre propre prédicteur de similarité d'image avec des résultats assez décents.
Le code complet peut être trouvé avec les images. ici.
A propos de l'auteur
Je m'appelle Prateek Agrawal et je suis un étudiant de troisième année à l'Indian Institute of Design and Manufacturing of Information Technology Kancheepuram., poursuivant mon double diplôme B.Tech et M.Tech en informatique. J'ai toujours eu un don pour l'apprentissage automatique et la science des données et je le pratique depuis environ un an et j'ai quelques victoires à mon actif..
Je crois personnellement que La passion est tout ce dont vous avez besoin. Je me souviens avoir eu peur d'entendre les gens parler de CNNS, RNN et Deep Learning parce que je ne pouvais pas comprendre une seule partie, mais je n'ai pas abandonné. J'ai eu la passion et j'ai commencé à faire de petits pas vers l'apprentissage et je publie ici mon premier blog. J'espère que vous avez apprécié cette lecture et que vous vous sentez un peu sûr de vous. Faites-moi confiance à ce sujet, si je peux, tu peux.
S'il vous plait, écrivez-moi en cas de questions ou juste pour dire bonjour.
LinkedIn: https://www.linkedin.com/in/prateekagrawal1405/
Github: https://github.com/prateekagrawaliiit
Crédits
- Wikipédia
- AnalytiqueL’analytique fait référence au processus de collecte, Mesurer et analyser les données pour obtenir des informations précieuses qui facilitent la prise de décision. Dans divers domaines, Comme les affaires, Santé et sport, L’analytique peut identifier des modèles et des tendances, Optimiser les processus et améliorer les résultats. L’utilisation d’outils et de techniques statistiques de pointe est essentielle pour transformer les données en connaissances applicables et stratégiques.... Vidhya
- Moitié
- Google images
Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.
