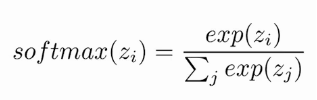Cibler
- La fonction de réveilLa fonction d’activation est un composant clé des réseaux de neurones, puisqu’il détermine la sortie d’un neurone en fonction de son entrée. Son objectif principal est d’introduire des non-linéarités dans le modèle, vous permettant d’apprendre des modèles complexes dans les données. Il existe différentes fonctions d’activation, comme le sigmoïde, ReLU et tanh, chacun avec des caractéristiques particulières qui affectent les performances du modèle dans différentes applications.... est l’un des composants de base de la neuronal rougeLes réseaux de neurones sont des modèles computationnels inspirés du fonctionnement du cerveau humain. Ils utilisent des structures appelées neurones artificiels pour traiter et apprendre des données. Ces réseaux sont fondamentaux dans le domaine de l’intelligence artificielle, permettant des avancées significatives dans des tâches telles que la reconnaissance d’images, Traitement du langage naturel et prédiction de séries temporelles, entre autres. Leur capacité à apprendre des motifs complexes en fait des outils puissants..
- Comprendre le fonctionnement de l'activation Softmax dans un problème de classification multiclasse
introduction
La fonction d'activation fait partie intégrante d'un réseau de neurones. Sans fonction réveil, un réseau de neurones est un modèle de régression linéaire simple. Cela signifie que la fonction d'activation accorde la non-linéarité au réseau de neurones.
Noter: Si vous êtes plus intéressé par l'apprentissage de concepts dans un format audiovisuel, nous avons cet article complet expliqué dans la vidéo ci-dessous. Si ce n'est pas comme ça, tu peux continuer à lire.
Si tu veux aller plus loin, Je vous recommande de lire l'article suivant.
Principes fondamentaux de la l'apprentissage en profondeurL'apprentissage en profondeur, Une sous-discipline de l’intelligence artificielle, s’appuie sur des réseaux de neurones artificiels pour analyser et traiter de grands volumes de données. Cette technique permet aux machines d’apprendre des motifs et d’effectuer des tâches complexes, comme la reconnaissance vocale et la vision par ordinateur. Sa capacité à s’améliorer continuellement au fur et à mesure que de nouvelles données lui sont fournies en fait un outil clé dans diverses industries, de la santé...: fonctionnalités d'activation et quand les utiliser
Dans cet article, nous discuterons de la fonction d'activation de SoftMax. Populairement utilisé pour les problèmes de classification multiclasse. Comprenons d'abord l'architecture du réseau de neurones pour un problème de classification multi-classes et aussi pourquoi d'autres fonctions d'activation ne peuvent pas être utilisées dans ce cas.
Exemple
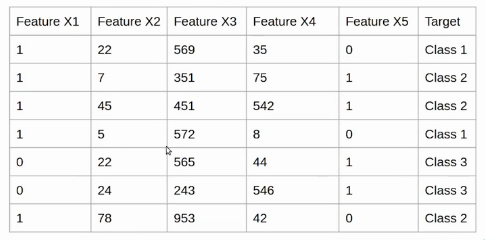
Supposons que nous ayons l'ensemble de données suivant et pour chaque observation, nous avons cinq fonctionnalités de FeatureX1 à FeatureX5 et le variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... de destination a trois classes.
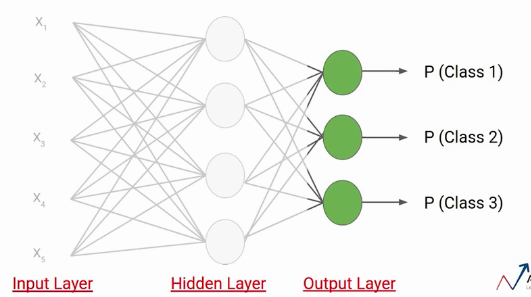
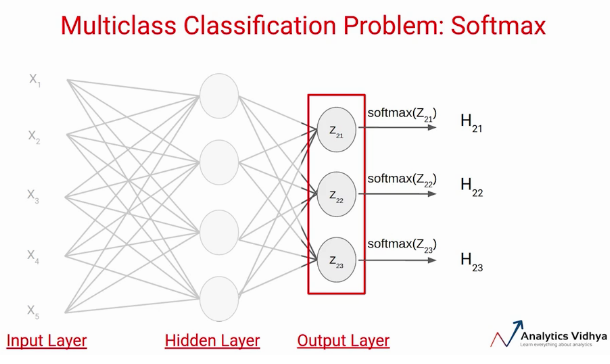
Créons maintenant un réseau de neurones simple pour ce problème. Ici, Nous avons un couche d'entréeLa "couche d'entrée" fait référence au niveau initial d’un processus d’analyse de données ou d’architectures de réseaux de neurones. Sa fonction principale est de recevoir et de traiter l’information brute avant qu’elle ne soit transformée par les couches suivantes. Dans le contexte de l’apprentissage automatique, Une bonne configuration de la couche d’entrée est cruciale pour garantir l’efficacité du modèle et optimiser ses performances dans des tâches spécifiques.... avec cinq neurones, puisque nous avons cinq caractéristiques dans l'ensemble de données. Ensuite, nous avons une couche cachée qui a quatre neurones. Chacun de ces neurones utilise des entrées, pondérations et biais ici pour calculer une valeur qui est représentée ici par Zij.
Par exemple, le premier neurone de la première couche est représenté par Z11 De même, le deuxième neurone de la première couche est représenté par Z12, et ainsi de suite.
Sur ces valeurs on applique la fonction d'activation. Disons une fonction d’activation tanh et envoyons les valeurs ou le résultat à la fonction Couche de sortieLa "Couche de sortie" est un concept utilisé dans le domaine des technologies de l’information et de la conception de systèmes. Il s’agit de la dernière couche d’un modèle logiciel ou d’une architecture qui est chargée de présenter les résultats à l’utilisateur final. Cette couche est cruciale pour l’expérience utilisateur, puisqu’il permet une interaction directe avec le système et la visualisation des données traitées.....
Le nombre de neurones dans la couche de sortie dépend du nombre de classes dans l'ensemble de données. Puisque nous avons trois classes dans l'ensemble de données, nous aurons trois neurones dans la couche de sortie. Chacun de ces neurones donnera la probabilité de classes individuelles. Cela signifie que le premier neurone vous donnera la probabilité que le point de données appartienne à la classe 1. de la même manière, le deuxième neurone vous donnera la probabilité que le point de données appartienne à la classe 2 et ainsi de suite.
Pourquoi pas sigmoïde?
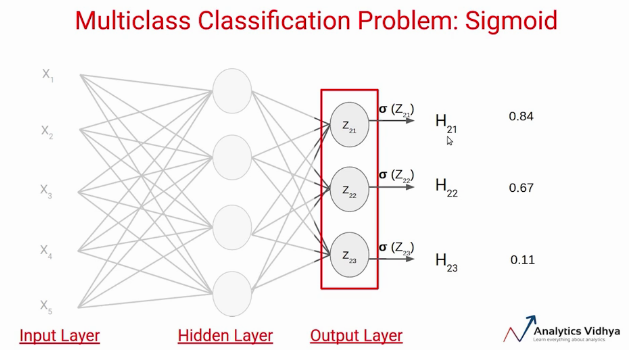
Supposons que nous calculions la valeur Z en utilisant les poids et les biais de cette couche et appliquions la fonction d'activation sigmoïde sur ces valeurs. On sait que la fonction d'activation sigmoïde donne la valeur entre 0 Oui 1. Supposons que ce soient les valeurs que nous obtenons en sortie.
Il y a deux problèmes dans ce cas:
Premier, si on applique un seuil de, Disons, 0.5, ce réseau dit que le point de données d'entrée appartient à deux classes. En second lieu, ces valeurs de probabilité sont indépendantes les unes des autres. Cela signifie la probabilité que le point de données appartienne à la classe 1 ne tient pas compte de la probabilité des deux autres classes.
C'est la raison pour laquelle la fonction d'activation sigmoïde n'est pas préférée dans les problèmes de classification de classes multiples..
Activation Softmax
Au lieu d'utiliser sigmoïde, nous utiliserons la fonction d'activation Softmax sur la couche de sortie dans l'exemple ci-dessus. La fonction de déclenchement Softmax calcule les probabilités relatives. Cela signifie qu'il utilise la valeur de Z21, Z22, Z23 pour déterminer la valeur de probabilité finale.
Voyons comment fonctionne réellement la fonction d'activation softmax. Similaire à la fonction d'activation sigmoïde, la Fonction SoftMaxLa fonction softmax est un outil mathématique utilisé dans le domaine de l’apprentissage automatique, Surtout dans les réseaux de neurones. Convertit un vecteur de valeur en une distribution de probabilité, Attribution de probabilités à chaque classe dans les problèmes multi-classifications. Sa formule normalise les sorties, s’assurer que la somme de toutes les probabilités est égale à un, permettre une interprétation efficace des résultats. Il est essentiel dans l’optimisation de... Renvoie la probabilité de chaque classe. Voici l'équation de la fonction d'activation SoftMax.
Ici, le Z représente les valeurs des neurones de la couche de sortie. L'exponentielle agit comme une fonction non linéaire. Plus tard ces valeurs sont divisées par la somme des valeurs exponentielles afin de les normaliser puis de les convertir en probabilités.
Notez que, quand le nombre de classes est de deux, devient la même que la fonction d'activation sigmoïde. En d'autres termes, sigmoïde est simplement une variante de la fonction Softmax. Si vous voulez plus d'informations sur ce concept, voir ce lien.
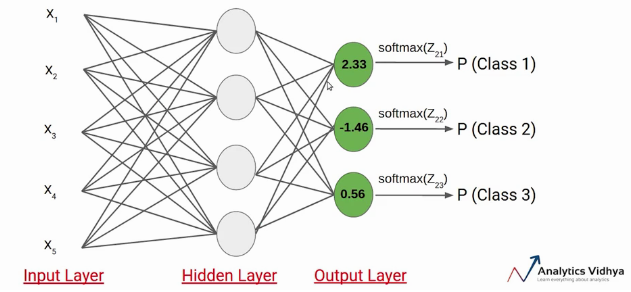
Comprenons avec un exemple simple comment fonctionne le softmax, nous avons le réseau de neurones suivant.
Supposons que la valeur de Z21, Z22, Z23 s'avère être 2,33, -1,46 Oui 0,56 respectivement. Maintenant la fonction d'activation SoftMax est appliquée à chacun de ces neurones et les valeurs suivantes sont générées.
Ce sont les valeurs de probabilité signalées par une donnée appartenant aux classes respectives. Notons que la somme des probabilités, dans ce cas, est égal à 1.
Dans ce cas, il est clair que l'entrée appartient à la classe 1. Ensuite, si la probabilité de l'une de ces classes change, la valeur de probabilité de la première classe changerait également.
Remarques finales
Il s'agit de la fonction d'activation de SoftMax dans cet article. Ici, nous avons vu pourquoi nous ne devrions pas utiliser de fonctions d'activation comme sigmoïde ou tanh dans les problèmes de classification multiclasse et aussi comment la fonction softmax fonctionne à travers un exemple.
Si vous cherchez à commencer votre parcours en science des données et que vous voulez tous les sujets sous un même toit, votre recherche s'arrête ici. Jetez un œil à l'IA et au ML BlackBelt certifiés de DataPeaker Plus Programme
Si vous avez des questions, faites le moi savoir dans les commentaires ci-dessous.
