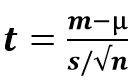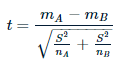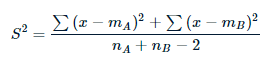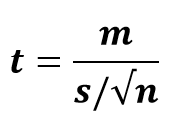introduction
"Vous ne pouvez pas tester une hypothèse; vous ne pouvez que l'améliorer ou le réfuter “. – Christophe Monckton
Chaque jour, nous nous retrouvons à essayer de nouvelles idées, trouver le chemin le plus rapide vers le bureau, le moyen le plus rapide de terminer notre travail ou simplement de trouver une meilleure façon de faire quelque chose que nous aimons. La question critique, ensuite, c'est si notre idée est significativement meilleure que ce que nous avons testé précédemment.
Ces idées qui nous viennent si régulièrement, c'est essentiellement ce qu'est une hypothèse. Et essayez ces idées pour découvrir laquelle fonctionne et laquelle est la meilleure à laisser de côté., ça s'appelle des tests d'hypothèses.
Les tests d'hypothèses sont l'une des choses les plus fascinantes que nous faisons en tant que scientifiques des données. Aucune idée n'est interdite à ce stade de notre projet. Personnellement, J'ai vu de nombreuses idées émerger des tests d'hypothèses, Des idées que la plupart d'entre nous auraient manquées sans cette étape !!
L'un des moyens les plus populaires de tester une hypothèse est un concept appelé test t.. Il existe différents types de tests t, comme nous le verrons bientôt, et chacun a sa propre application unique. Si vous êtes un aspirant data scientist, vous devez savoir ce qu'est un test t et quand vous pouvez en profiter.
Ensuite, dans cet article, Nous découvrirons les différentes nuances d'un test t, puis nous examinerons les trois types de tests t différents.. Glaçage sur le gateau? Nous allons implémenter chaque type de test t dans R pour visualiser leur fonctionnement dans des scénarios pratiques. Allons-y!
Noter: vous devriez lire l'article ci-dessous si vous avez besoin de rafraîchir les concepts de test d'hypothèse:
Table des matières
- Quand devons-nous effectuer un test t?
- Hypothèses pour effectuer un test t
- Types de tests t (avec des exemples élaborés en R)
- Test T pour un échantillon
- Test t indépendant pour deux échantillons
- Test t d'échantillons appariés
Quand devons-nous effectuer un test t?
Commençons par comprendre où un test t peut être utilisé avant de plonger dans ses différents types et implémentations.. Je crois fermement que la meilleure façon d'apprendre un concept est de le visualiser à travers un exemple. Prenons donc un exemple simple pour voir où un test t est utile.
Considérons une entreprise de télécommunications qui a deux centres de services dans la ville. L'entreprise veut savoir si le temps moyen nécessaire pour servir un client est le même dans les deux magasins.
La source: Ateliers
L'entreprise mesure le temps moyen qu'il lui faut 50 clients aléatoires dans chaque magasin. Le magasin A prend 22 minutes, tandis que le magasin B a une moyenne de 25 minutes. Peut-on dire que le magasin A est plus efficace que le magasin B en termes de service client?
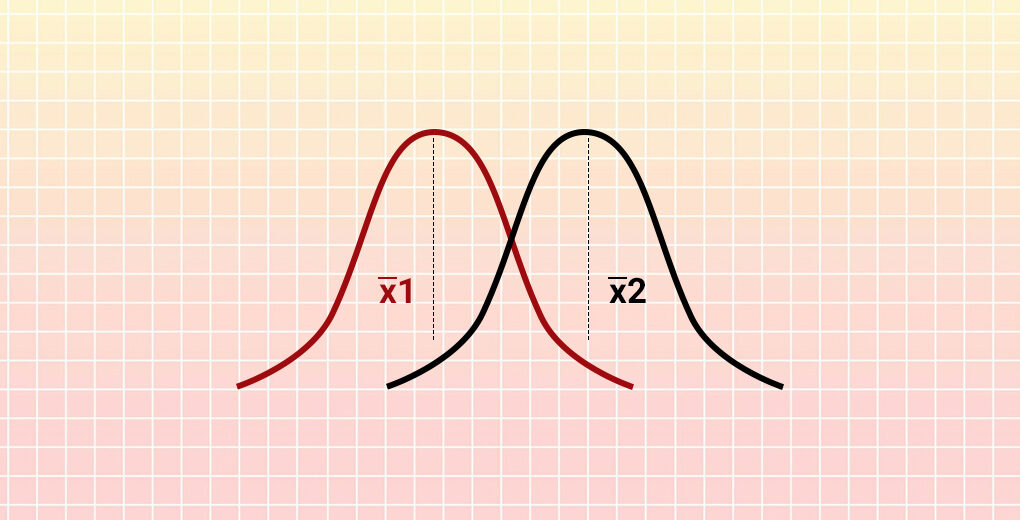
Cela ressemble à ça, non? Cependant, nous avons seulement analysé 50 clients aléatoires des nombreuses personnes qui visitent les magasins. Le simple fait de regarder le temps d'échantillonnage moyen peut ne pas être représentatif de tous les clients visitant les deux magasins.
C'est là qu'intervient le test t.. Cela nous aide à comprendre si la différence entre deux moyennes d'échantillon est vraiment réelle ou est simplement due au hasard.
Hypothèses pour effectuer un test t
Il y a certaines hypothèses que nous devons garder à l'esprit avant d'effectuer un test t:
- Les données doivent suivre une échelle continue ou ordinale (résultats des tests de QI des élèves, par exemple)
- Les observations dans les données doivent être sélectionnées au hasard
- Les données doivent ressembler à une courbe en forme de cloche lorsqu'elles sont tracées, c'est-à-dire, devrait être normalement distribué. Vous pouvez vous référer à cet article pour mieux comprendre la distribution normale
- Une grande taille d'échantillon doit être prise pour rapprocher les données d'une distribution normale (unbien que le test t soit essentiel pour les petits échantillons car ses distributions ne sont pas normales)
- Les variations entre les groupes doivent être égales (Fou test t indépendant à deux échantillons)
Ensuite, Quels sont les différents types de tests t? Quand devons-nous effectuer chaque type? Nous répondrons à ces questions dans la section suivante et verrons comment nous pouvons effectuer chaque type de test t dans R.
Types de tests t (avec des exemples élaborés en R)
Il existe trois types de tests t que nous pouvons effectuer sur la base des données disponibles:
- Test t à un échantillon
- Test t indépendant à deux échantillons
- Test t d'échantillons appariés
Dans cette section, nous allons voir chacun de ces types en détail. J'ai également fourni le code R pour chaque type de test t afin que vous puissiez les suivre pendant que nous les implémentons. C'est un excellent moyen d'apprendre et de voir à quel point ces tests t sont utiles !!
Test T pour un échantillon
Dans un test t à un échantillon, nous comparons la moyenne (ou moyenne) d'un groupe avec la moyenne (ou moyenne) s'est installé. Cette moyenne établie peut être n'importe quelle valeur théorique (ou il peut s'agir de la moyenne de la population).
Considérons l'exemple suivant: un chercheur veut déterminer si le temps moyen pour manger un hamburger (taille standard) diffère d'une valeur définie. Disons que cette valeur est 10 minutes. Comment pensez-vous que le chercheur peut déterminer cela?
Il / elle peut largement suivre les étapes suivantes:
- Sélectionnez un groupe de personnes
- Enregistrez le temps de consommation individuel d'un hamburger de taille standard.
- Calculer l'heure moyenne des repas du groupe.
- Finalement, comparer cette valeur moyenne avec la valeur de consigne de 10
En peu de mots, c'est ainsi que nous pouvons effectuer un test t d'un échantillon. Voici la formule pour le calculer:
où,
- t = t statistique
- m = moyenne du groupe
- µ = valeur théorique ou moyenne de la population
- s = écart type du groupe
- n = taille du groupe ou taille de l'échantillon
Noter: Comme mentionné ci-dessus dans les hypothèses selon lesquelles une grande taille d'échantillon doit être prise pour que les données approchent d'une distribution normale. (Bien que le test t soit essentiel pour les petits échantillons car ses distributions ne sont pas normales).
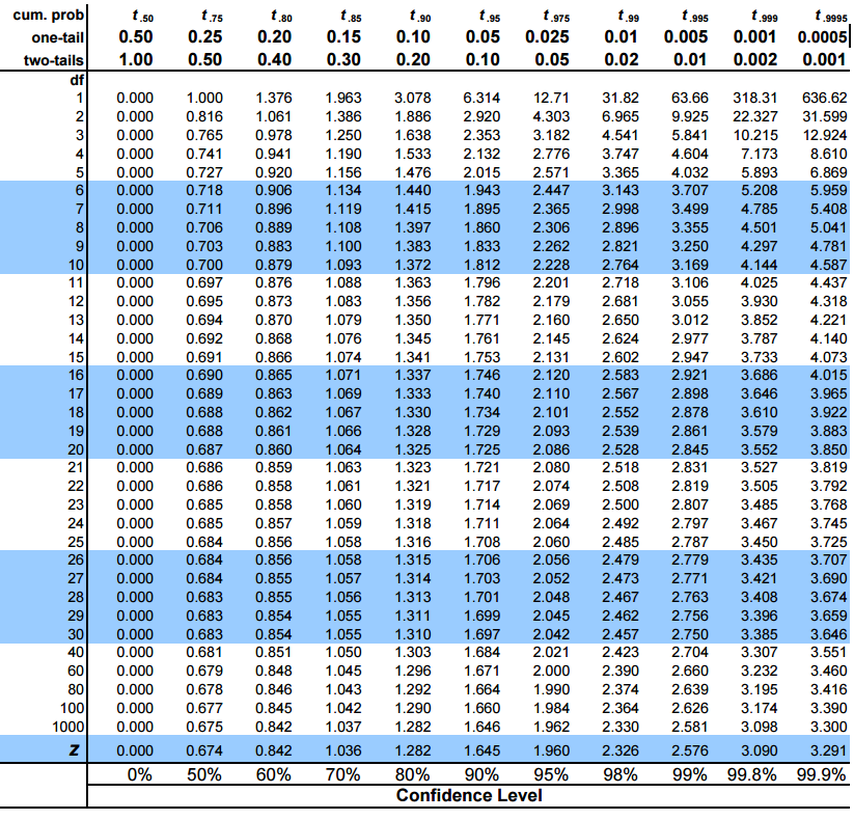
Une fois que nous avons calculé la valeur de la statistique t, la tâche suivante consiste à le comparer avec la valeur critique du test t. Nous pouvons trouver cela dans le tableau suivant du test t contre le degré de liberté (n-1) et le niveau d'importance:
Cette méthode permet de vérifier si la différence entre les moyennes est statistiquement significative ou non.. Consolidons davantage notre compréhension d'un test t à un échantillon en l'effectuant sur R.
Implémentation du test t à un échantillon dans R
Une entreprise de fabrication de mobiles a prélevé un échantillon de mobiles du même modèle à partir des données du mois précédent. Ils veulent vérifier si la taille moyenne de l'écran de l'échantillon diffère de la longueur souhaitée de 10 cm. Vous pouvez télécharger les données ici.
Paso 1: Premier, importer les données.
Paso 2: Validez-le pour qu'il soit correct dans R:
Production:
#Nombre de lignes et de colonnes [1] 1000 1 > #Voir en haut 10 lignes de l'ensemble de données Screen_size.in.cm. 1 10.006692 2 10.081624 3 10.072873 4 9.954496 5 9.994093 6 9.952208 7 9.947936 8 9.988184 9 9.993365 10 10.016660
Paso 3: Rappelez-vous les hypothèses que nous avons discutées plus tôt? Nous devons les revoir:
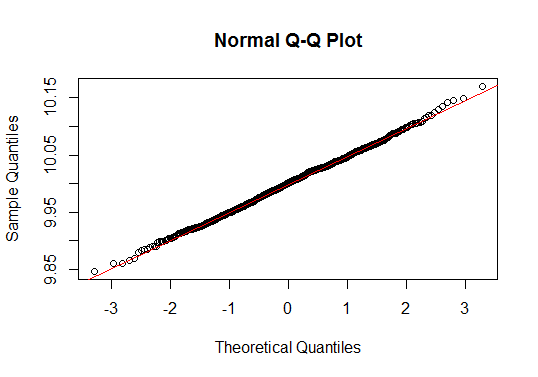
On obtient le graphe QQ suivant:
Presque toutes les valeurs sont sur la ligne rouge. Nous pouvons dire sans risque que les données suivent une distribution normale.
Paso 4: Effectuer un test t à un échantillon:
Production:
Test t à un échantillon Les données: data$Screen_size.in.cm. t = -0.39548, df = 999, valeur p = 0.6926 hypothèse alternative: la vraie moyenne n'est pas égale à 10 95 intervalle de confiance en pourcentage: 9.996361 10.002418 exemples d'estimations: moyenne de x 9.99939
La statistique t s'avère être -0,39548. Notez qu'ici on peut traiter les valeurs négatives comme leur contrepartie positive. À présent, se référer au tableau mentionné ci-dessus pour la valeur t critique. Le degré de liberté est ici 999 et l'intervalle de confiance est 95%.
La valeur critique t est 1,962. Puisque la statistique t est inférieure à la valeur t critique, no rechazamos la hypothèse nulleLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos.... y podemos concluir que el tamaño de pantalla promedio de la muestra no difiere de 10 cm.
Nous pouvons également vérifier cela à partir de la valeur p, qui est supérieur à 0.05. Donc, on ne rejette pas l'hypothèse nulle dans un intervalle de confiance du 95%.
Test t indépendant à deux échantillons
Le test t à deux échantillons est utilisé pour comparer les moyennes de deux échantillons différents.
Disons que nous voulons comparer la taille moyenne des employés masculins avec la taille moyenne des femmes. Bien sûr, le nombre d'hommes et de femmes doit être égal pour cette comparaison. C'est là qu'un test t à deux échantillons est utilisé.
Voici la formule pour calculer la statistique t pour un test t à deux échantillons:
où,
- métroUNE y MB sont les moyennes de deux échantillons différents
- NordUNE et nB sont les tailles d'échantillon
- S2 c'est un estimadorLe "Estimateur" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... de la varianza común de dos muestras, Quoi:
Ici, le degré de liberté est nUNE + mB – 2.
Nous suivrons la même logique que celle que nous avons vue dans un test t à un échantillon pour vérifier si la moyenne d'un groupe est significativement différente de celle d'un autre groupe.. C'est comme ca, nous comparerons la statistique t calculée avec la valeur t critique.
Prenons un exemple de test t indépendant à deux échantillons et résolvons-le dans R.
Implémentation du test t à deux échantillons dans R
Pour cette rubrique, nous allons travailler avec des données sur deux échantillons des différents modèles d'un téléphone mobile. Nous voulons vérifier si la taille moyenne de l'écran de l'échantillon 1 diffère de la taille moyenne de l'écran de l'échantillon 2. Vous pouvez télécharger les données ici.
Paso 1: Encore, importer d'abord les données.
Paso 2: Validez-le pour qu'il soit correct dans R:
Paso 3: Nous devons vérifier les hypothèses comme nous l'avons fait ci-dessus. Je vais laisser cet exercice entre tes mains maintenant.
En outre, dans ce cas, on va vérifier l'homogénéité de la variance:
Production:
#Homogénéité de la variance > où(data$screensize_sample1) [1] 0.00238283 > où(data$screensize_sample2) [1] 0.002353585
Génial, les variantes sont les mêmes. Nous pouvons avancer.
Paso 4: Effectuer le test t des deux échantillons indépendants:
Noter: Réécrivez le code ci-dessus avec "var.equal = F" si vous obtenez des variations inégales ou inconnues. Ce sera un cas de test de t de Welch qui est utilisé pour comparer les moyennes de deux échantillons avec des variances inégales.
Production:
Test t à deux échantillons Les données: data$screensize_sample1 et data$screensize_sample2 t = 1.3072, df = 1998, valeur p = 0.1913 hypothèse alternative: la vraie différence de moyenne n'est pas égale à 0 95 intervalle de confiance en pourcentage: -0.001423145 0.007113085 exemples d'estimations: moyenne de x moyenne de y 10.000976 9.998131
Que pouvez-vous déduire du résultat ci-dessus? Nous pouvons confirmer que la statistique t est à nouveau inférieure à la valeur critique t, donc on ne rejette pas l'hypothèse nulle. Donc, nous pouvons conclure qu'il n'y a pas de différence entre la taille moyenne de l'écran des deux échantillons.
Nous pouvons le vérifier à nouveau en utilisant la valeur p. s'avère être supérieur à 0.05, donc, on ne rejette pas l'hypothèse nulle dans un intervalle de confiance du 95%. Il n'y a pas de différence entre la moyenne des deux échantillons.
Test t d'échantillons appariés
Le test t pour échantillons appariés est assez intrigant. Ici, on mesure un groupe à deux moments différents. Nous comparons des moyennes distinctes pour un groupe à deux moments différents ou dans deux conditions différentes. Confus? Laisse-moi expliquer.
Un certain manager a remarqué que le niveau de productivité de ses employés avait une tendance significative à la baisse. Ce gestionnaire a décidé de réaliser un programme de formation pour tous ses employés afin d'augmenter leur niveau de productivité.
Comment le gestionnaire mesurera-t-il si les niveaux de productivité ont augmenté ?? Est simple: il suffit de comparer le niveau de productivité des employés avant et après le programme de formation.
Ici, nous comparons le même échantillon (les employés) à deux moments différents (avant et après la formation). Ceci est un exemple de test t apparié. La formule de calcul de la statistique t pour un test t apparié est:
où,
- t = t statistique
- m = moyenne du groupe
- µ = valeur théorique ou moyenne de la population
- s = écart type du groupe
- n = taille du groupe ou taille de l'échantillon
Nous pouvons prendre le degré de liberté dans ce test comme n – 1 puisqu'un seul groupe est impliqué. À présent, résolvons un exemple dans R.
Implémentation du test t apparié dans R
Le directeur d'une entreprise de fabrication de pneus veut comparer le matériau en caoutchouc de deux lots de pneus. Une façon de faire cela: vérifier la différence entre les kilomètres moyens parcourus par un lot de pneus jusqu'à leur usure.
Vous pouvez télécharger les données de ici. j'ai compris!
Paso 1: Premier, importer les données.
Paso 2: Validez-le pour qu'il soit correct dans R:
Paso 3: Maintenant, nous vérifions les hypothèses comme nous l'avons fait dans un test t à un échantillon. De nouveau, je te laisse ça.
Paso 4: Effectuer le test t apparié:
Production:
Test t apparié Les données: data$tyre_1 et data$tyre_2 t = -5.2662, df = 24, valeur p = 2.121e-05 hypothèse alternative: la vraie différence de moyenne n'est pas égale à 0 95 intervalle de confiance en pourcentage: -2201.6929 -961.8515 exemples d'estimations: moyenne des différences -1581.772
Vous devez être un expert pour déchiffrer cette sortie maintenant !! La valeur p est inférieure à 0.05. On peut rejeter l'hypothèse nulle avec un intervalle de confiance de 95% et conclure qu'il existe une différence significative entre les moyennes des pneus avant et après le remplacement du matériau en caoutchouc.
La moyenne négative de la différence montre que les kilomètres moyens parcourus par le pneu 2 sont plus que la moyenne des kilomètres parcourus par le pneu 1.
Remarques finales
Dans cet article, nous avons appris le concept du test t, ses hypothèses et aussi les trois différents types de tests t avec leurs implémentations dans R. Le test t a à la fois une signification statistique et des applications pratiques dans le monde réel.. .
Si vous débutez en statistiques, vous voulez couvrir vos bases et vous voulez aussi vous lancer dans la science des données, Je vous recommande de prendre le Cours d'introduction à la science des données. Vous donne un aperçu complet des statistiques descriptives et inférentielles avant de plonger dans les techniques de la science des données.
Avez-vous trouvé cet article utile? Pouvez-vous penser à d'autres applications du test t?? Faites-le moi savoir dans la section commentaire ci-dessous et nous pourrons avoir plus d'idées!!
