Statistiques de commande | Quelles sont les statistiques de commande?

introduction

La statistique des commandes est un concept très utile en science statistique. Ils ont un large éventail d'applications, y compris la modélisation d'enchères, courses automobiles et polices d'assurance, optimisation des processus de production, estimación de paramètresLes "paramètres" sont des variables ou des critères qui sont utilisés pour définir, mesurer ou évaluer un phénomène ou un système. Dans divers domaines tels que les statistiques, Informatique et recherche scientifique, Les paramètres sont essentiels à l’établissement de normes et de standards qui guident l’analyse et l’interprétation des données. Leur sélection et leur manipulation correctes sont cruciales pour obtenir des résultats précis et pertinents dans toute étude ou projet.... de distribuciones, et al. A travers cet article, on comprendra l'idée de statistiques de commandes. Nous allons d'abord comprendre sa signification et procéder progressivement à sa diffusion., couvrant éventuellement des concepts plus avancés.

Supposons que nous ayons un ensemble de variables aléatoires X₁, X₂, …, X_Nord, indépendantes et distribuées de manière identique (iid). Pour l'indépendance, queremos decir que el valor tomado por una variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... aleatoria no está influenciado por los valores tomados por otras variables aleatorias. Par répartition identique, nous voulons dire que la fonction de densité de probabilité (PDF) (ou équivalent, la fonction de distribution cumulative, CDF) pour les variables aléatoires c'est pareil. Le K^e La statistique d'ordre pour cet ensemble de variables aléatoires est définie comme k^e plus petite valeur d'échantillon.

Pour mieux comprendre ce concept, nous prendrons 5 variables aléatoires X₁, X₂, X₃, X₄, X₅. On observera une réalisation / résultat aléatoire de la distribution de chacune de ces variables aléatoires. Supposons que nous obtenions les valeurs suivantes:

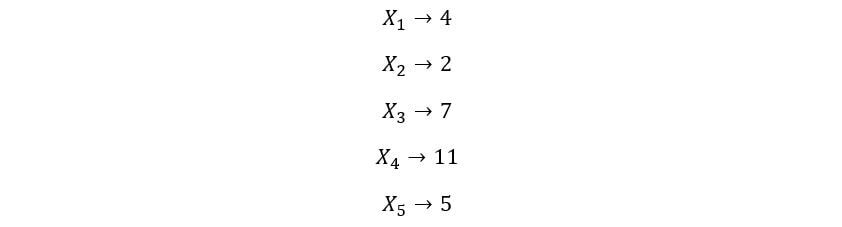
Le K^e la statistique d'ordre pour cette expérience est k^e plus petite valeur de l'ensemble {4, 2, 7, 11, 5}. Ensuite, les 1^{S t} la statistique de commande est 2 (plus petite valeur), la 2^{Dakota du nord} la statistique de commande est 4 (le plus petit suivant), et ainsi de suite. Le 5^e la statistique d'ordre est la cinquième plus petite valeur (la plus grande valeur), Qu'est que c'est 11. Nous répétons ce processus plusieurs fois, c'est-à-dire, nous extrayons des échantillons de la distribution de chacune de ces variables aléatoires iid et trouvons le k^e plus petite valeur pour chaque ensemble d'observations. La distribution de probabilité de ces valeurs donne la distribution de k^e statistiques de commande.

En général, si on commande des variables aléatoires X₁, X₂, …, X_Nord Dans l'ordre croissant, puis le k^e la statistique de la commande est affichée comme:

La notation générale du k^e la statistique de commande est X_(k). Remarque X_(k) est différent de X_k. X_k est le k^e variable aléatoire de notre ensemble, tandis que X_(k) est le k^e ordre statistique de notre ensemble. X_(k) prend la valeur de X_k oui X_k est le k^e Variable aléatoire lorsque les réalisations sont triées par ordre croissant.

Le 1^{S t} statistique d'ordre X₍₁₎ est l'ensemble des valeurs minimales de la réalisation de l'ensemble de 'n’ Variables aléatoires. Alors^e statistique d'ordre X_(Nord) est l'ensemble des valeurs maximales (nième valeurs minimales) de la réalisation de l'ensemble de 'n’ Variables aléatoires. Ils peuvent être exprimés comme:

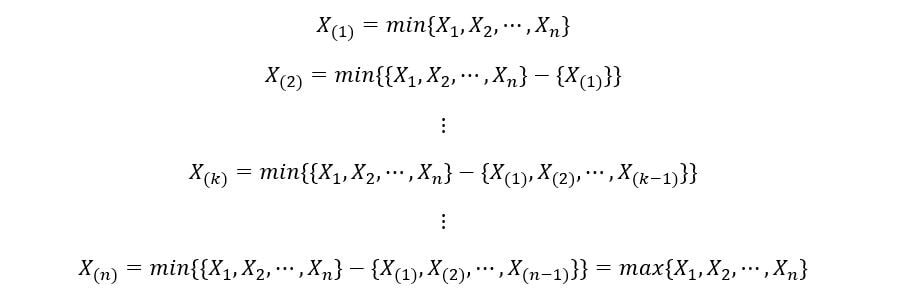
Distribution des statistiques de commande

Nous allons maintenant essayer de connaître la répartition des statistiques de commande. Nous allons d'abord décrire la distribution des n^e statistiques de commande, Puis il 1^{S t} ordre statistique et enfin le k^e statistiques générales sur les commandes.

UNE) Répartition de n^e Statistiques de commande:

Soit la fonction de densité de probabilité (PDF) et la fonction de distribution cumulative (CDF) nos variables aléatoires laisser f_X(X) oui F_X(X) respectivement. Par définition de CDF,

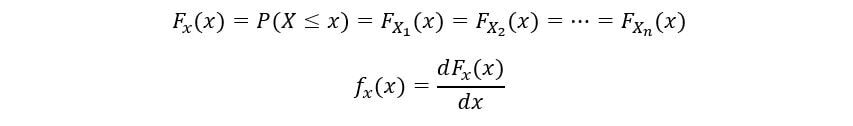
Puisque nos variables aléatoires sont distribuées de manière identique, avoir le même PDF f_X(X) y CDF F_X(X). Nous allons maintenant calculer la CDF de n^e statistiques de commande (F_Nord(X)) comme suit:

Variables aléatoires X₁, X₂, …, X_Nord ils sont aussi indépendants. Pourtant, par propriété d'indépendance,

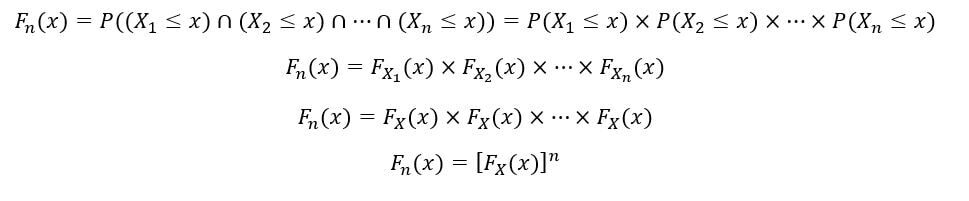
Le PDF du n^e ordre statistique (F_Nord(X)) est calculé comme suit:

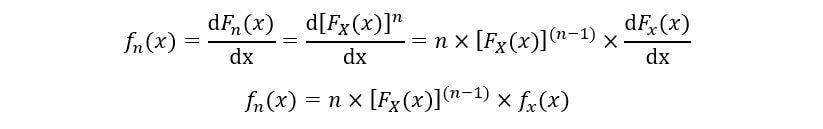
Donc, l'expression pour PDF et CDF de n^e La statistique de commande a été obtenue.

B) Distribution de 1^{S t} Statistiques de commande:

Le CDF d'une variable aléatoire peut également être calculé comme le un moins la probabilité que la variable aléatoire X prenne une valeur supérieure ou égale à x. Mathématiquement,

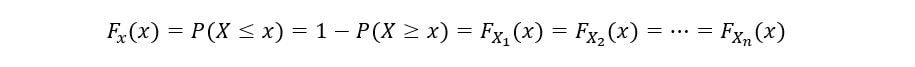
Nous déterminerons le CDF de 1^{S t} statistiques de commande (F₁(X)) comme suit:

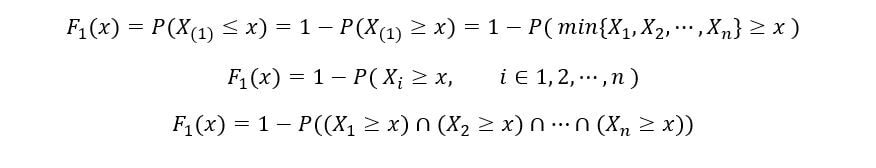
Une fois de plus, en utilisant la propriété d'indépendance des variables aléatoires,

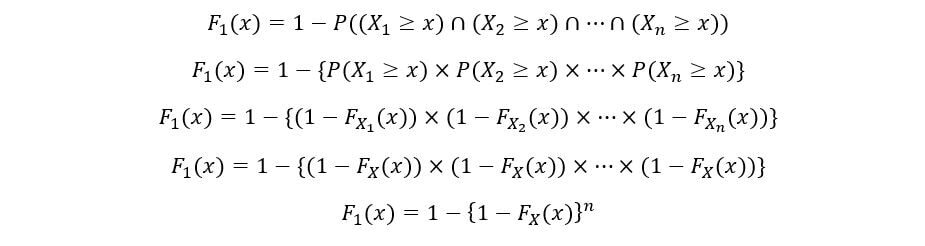
Le PDF du 1^{S t} ordre statistique (F₁(X)) est calculé comme suit:

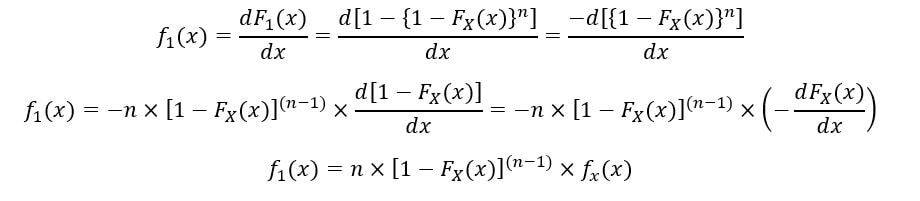
Donc, l'expression pour PDF et CDF de 1^{S t} La statistique de commande a été obtenue.

C) Répartition du k^e Statistiques de commande:

Fourchette^e statistiques de commande, en général, l'équation suivante décrit votre CDF (F_k(X)):

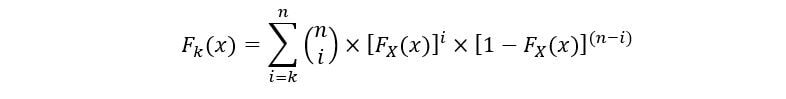
Le PDF de k^e ordre statistique (F_k(X)) est exprimé comme:

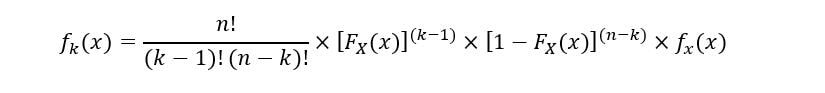
Pour éviter les confusions, nous utiliserons des preuves géométriques pour comprendre l'équation. Comme discuté ci-dessus, l'ensemble des variables aléatoires a le même PDF (F_X(X)). Le graphique ci-dessous montre un exemple de PDF avec le k^e Statistique d'ordre obtenue à partir d'un échantillonnage aléatoire:

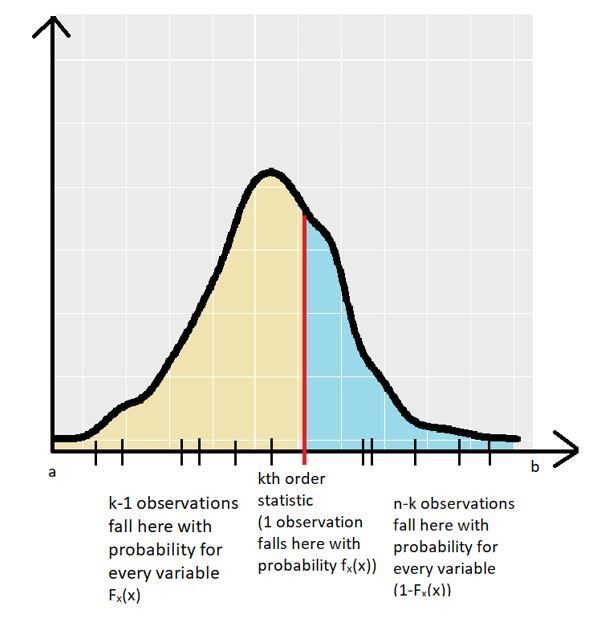
Ensuite, le PDF des variables aléatoires f_X(X) est défini entre l'intervalle [une,b]. La statistique d'ordre k pour un échantillon aléatoire est indiquée par la ligne rouge. Les autres réalisations variables (pour l'échantillon aléatoire) représenté par les petites lignes noires sur l'axe des x.

Il y a exactement (k – 1) observations de variables aléatoires qui tombent dans la région jaune du graphique (la région entre & k^e statistiques de commande). La probabilité qu'une observation particulière tombe dans cette région est donnée par le CDF des variables aléatoires (F_X(X)). Mais nous sommes conscients que (k – 1) les observations sont tombées dans la région, ce qui nous donne le terme (pour l'indépendance) (F_X(X))^{(k – 1)}.

Il y a exactement (m – k) observations de variables aléatoires qui tombent dans la région bleue du graphique (la région entre k^e ordre statistique & b). La probabilité qu'une observation particulière tombe dans cette région est donnée par le 1 – CDF des variables aléatoires (1- F_X(X)). Mais nous sommes conscients que (m – k) les observations sont tombées dans la région, ce qui nous donne le terme (pour l'indépendance) (1-F_X(X))^{(m – k)}.

Finalement, exactement 1 l'observation tombe exactement sur la statistique d'ordre k avec une probabilité f_X(X). Donc, le produit de 3 termes nous donne une idée de la signification géométrique de l'équation pour PDF de la statistique d'ordre k. Mais, D'où vient le terme factoriel? Le scénario ci-dessus n'a montré qu'une des nombreuses commandes. Il peut y avoir plusieurs de ces combinaisons. Le nombre total de ces combinaisons est indiqué ci-dessous:

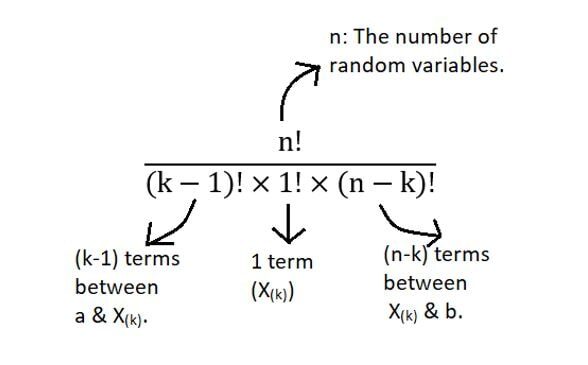
Pourtant, le produit de tous ces termes nous donne la distribution générale de k^e statistiques de commande.

Fonctions utiles des statistiques de commandes

Les statistiques de commande mènent à plusieurs fonctions utiles. Entre eux, los notables incluyen el rango de la muestra y la médianLa médiane est une mesure statistique qui représente la valeur centrale d’un ensemble de données ordonnées. Pour le calculer, Les données sont organisées de la plus basse à la plus élevée et le numéro au milieu est identifié. S’il y a un nombre pair d’observations, La moyenne des deux valeurs fondamentales est calculée. Cet indicateur est particulièrement utile dans les distributions asymétriques, puisqu’il n’est pas affecté par les valeurs extrêmes.... de la muestra.

1) Gamme d'échantillons: Il est défini comme la différence entre la plus grande et la plus petite valeur. Il s'exprime comme suit:

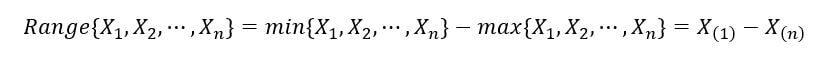
2) Médiane de l'échantillon: La médiane de l'échantillon divise l'échantillon aléatoire (réalisations de l'ensemble des variables aléatoires) en deux moitiés, l'un contenant les échantillons de valeur la plus faible et l'autre contenant les échantillons de valeur la plus élevée. C'est comme la statistique d'ordre intermédiaire / central. Il est mathématiquement défini comme:

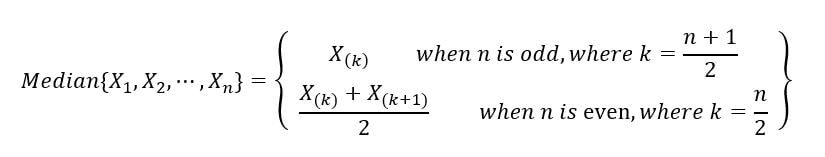
Ensemble de statistiques de commande PDF

Une fonction de densité de probabilité conjointe peut nous aider à mieux comprendre la relation entre deux variables aléatoires (statistiques à deux ordres
dans notre cas). L'ensemble PDF pour toutes les statistiques de 2 X commandes_(une) & X_(B), tel que 1 ≤ a ≤ b ≤ n est donné par l'équation suivante:

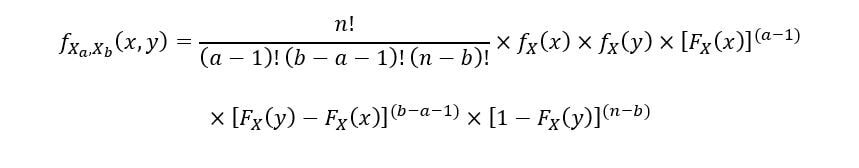
Exemple

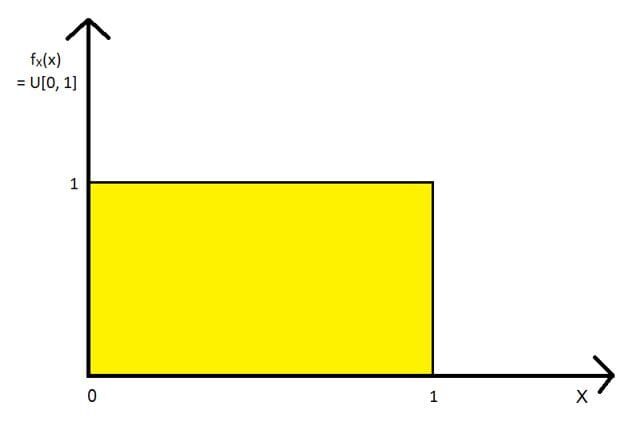
Nous allons utiliser un exemple très simple pour illustrer la répartition des statistiques de commandes: la distribution uniforme standard (U[0, 1] Distribution). Nous prendrons 5 variables aléatoires X₁, X₂, X₃, X₄, X₅, tout le monde a le U[0, 1] Distribution. Pour cet ensemble de variables aléatoires, nous allons calculer et tracer le 1^{S t}, 3^rd (la médiane de l'échantillon) Oui 5^e (Nord^e) statistiques de commande. La siguiente chiffre"Chiffre" est un terme utilisé dans divers contextes, De l’art à l’anatomie. Dans le domaine artistique, fait référence à la représentation de formes humaines ou animales dans des sculptures et des peintures. En anatomie, désigne la forme et la structure du corps. En outre, en mathématiques, "chiffre" Il est lié aux formes géométriques. Sa polyvalence en fait un concept fondamental dans de multiples disciplines.... muestra la U[0, 1] Distribution:

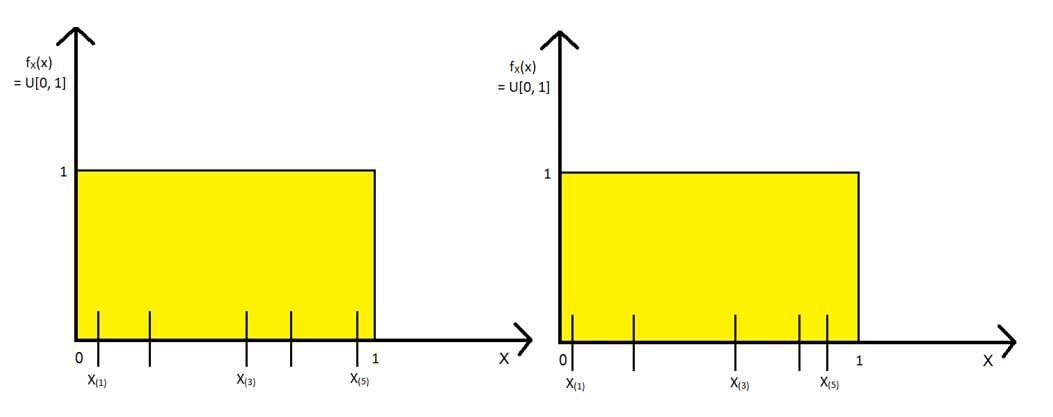
Nous allons tirer des échantillons aléatoires comme suit et trouver le 1^{S t}, 3^rd & 5^e statistique de commande pour chaque échantillon. Vous trouverez ci-dessous deux des échantillons:

La distribution uniforme standard PDF et CDF sont données comme:

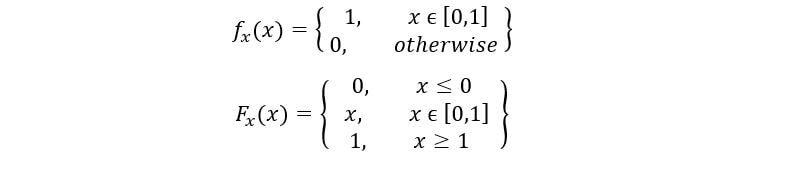
Nous utiliserons ces informations et calculerons X₍₁₎, X₍₃₎ & X₍₅₎ en utilisant les formules que nous avons dérivées. Nous ne prendrons le cas que lorsque x est compris entre 0 Oui 1 (pour les autres cas, la statistique de commande est nulle puisque PDF est nul).

UNE) À 1^{S t} statistiques de commande:

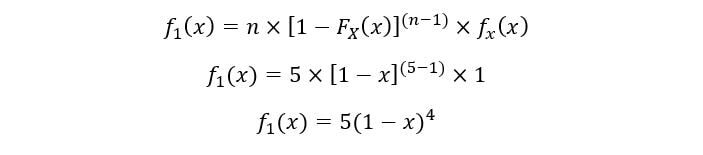
Terrain pour f₁(X):

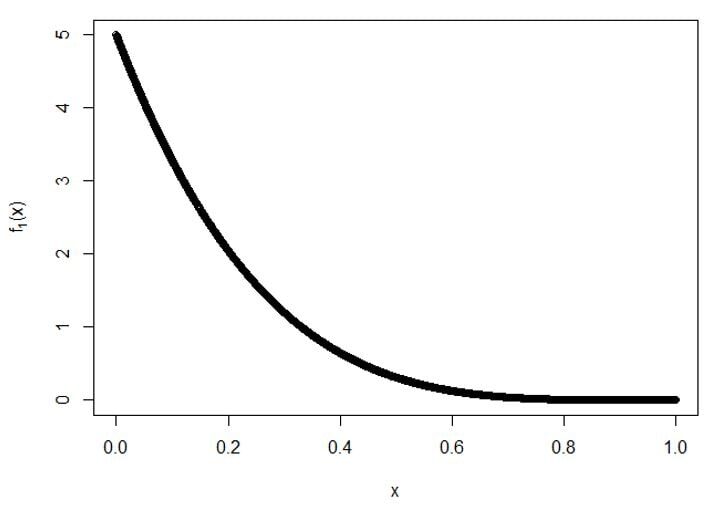
B) À 3^rd statistiques de commande:

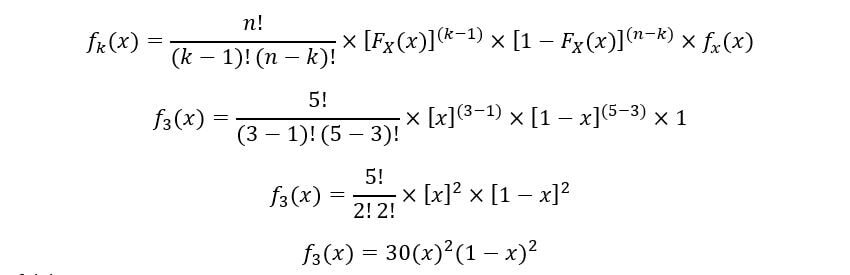
Terrain pour f₅(X):

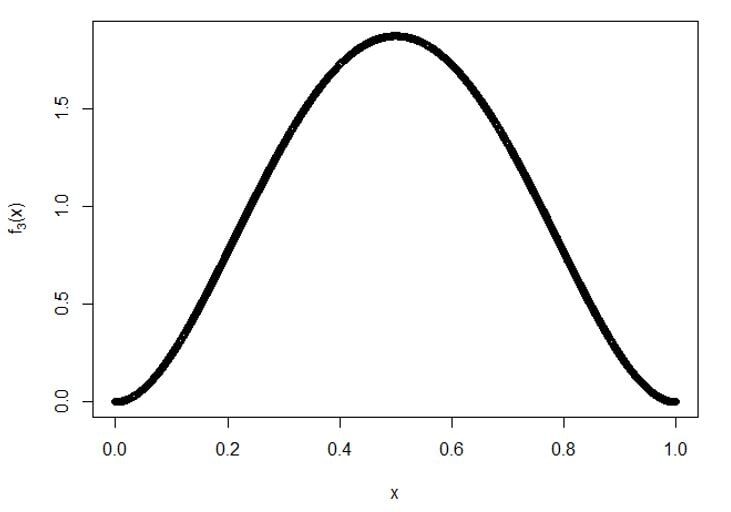
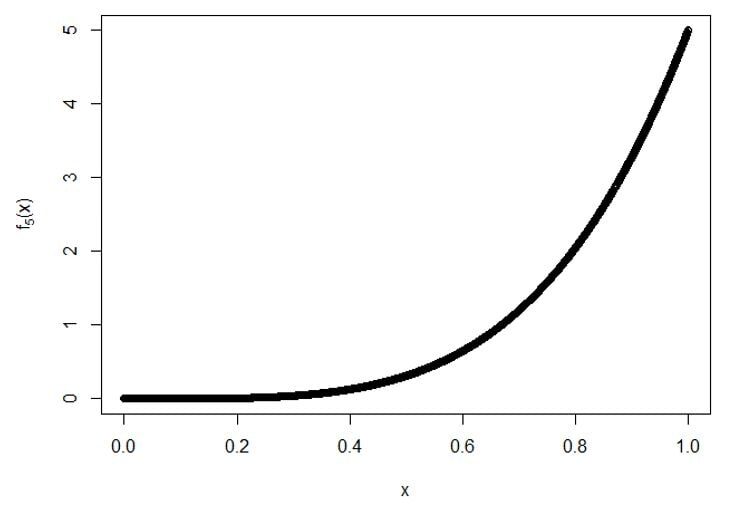
C) À 5^e statistiques de commande:

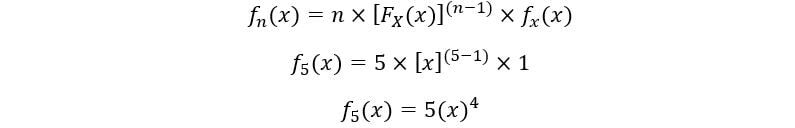
Terrain pour f₅(X):

conclusion

Donc, nous avons exploré les concepts de statistiques d'ordre en profondeur. Un large éventail de processus physiques peut être modélisé grâce aux statistiques de commande, exploiter ses propriétés, en particulier leurs distributions.

Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.

En rapport