Grandi dati

Coefficiente di correlazione di Pearson: una guida per principianti

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.

introduzione

Consideriamo l'esempio del rilevamento del prezzo dell'auto in cui dobbiamo rilevare il prezzo considerando tutte le variabili che influenzano il prezzo dell'auto, come la lunghezza della macchina, peso a vuoto, l'altezza della macchina, la larghezza dell'auto, il tipo di carburante, il corpo, il potere, eccetera.

La correlazione tra variabili continue può essere trovata usando Python:

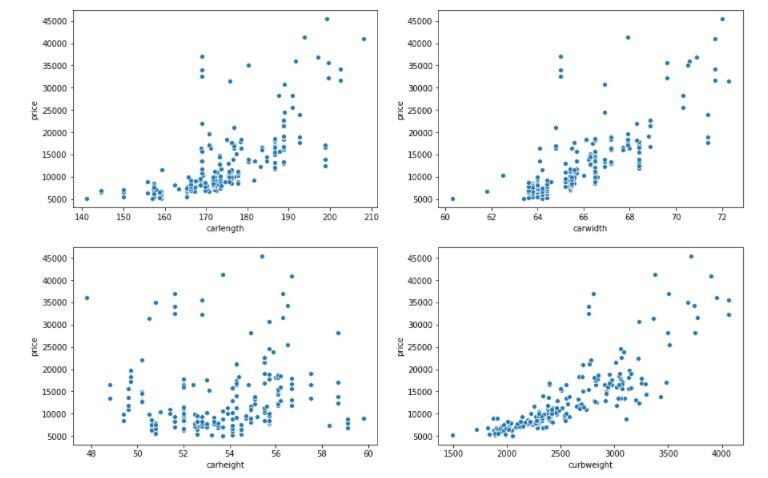
Possiamo vedere nel Diagramma di dispersioneIl grafico a dispersione è uno strumento grafico utilizzato in statistica per visualizzare la relazione tra due variabili. Consiste in un insieme di punti in un piano cartesiano, dove ogni punto rappresenta una coppia di valori corrispondenti alle variabili analizzate. Questo tipo di grafico consente di identificare i modelli, Tendenze e possibili correlazioni, facilitare l'interpretazione dei dati e il processo decisionale sulla base delle informazioni visive presentate.... anteriore, poiché la lunghezza della macchina, il peso a vuoto e la larghezza dell'auto aumentano, aumenta anche il prezzo dell'auto. Quindi, possiamo dire che esiste una correlazione positiva tra le tre variabili precedenti con il prezzo dell'auto. Qui, vediamo anche che non c'è correlazione tra l'altezza dell'auto e il prezzo dell'auto.

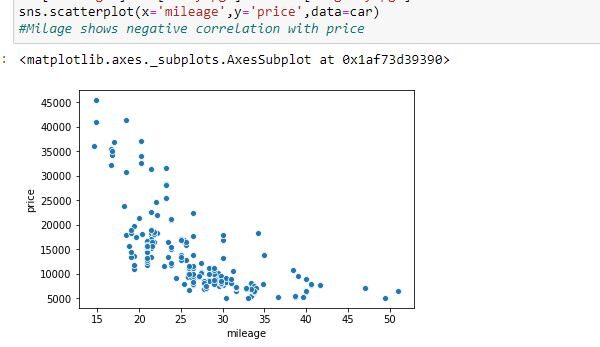
Le auto costose hanno un chilometraggio notevolmente ridotto rispetto alle auto di fascia bassa. Perciò, in questo caso, possiamo dire che c'è una correlazione negativa tra il prezzo dell'auto e il chilometraggio.

Definizione

Concentriamoci su una spiegazione statistica di esso. Il coefficiente di correlazione di Pearson è rappresentato come "r", misura quanto è forte l'associazione lineare tra due variabili continue usando la formula:

I valori di correlazione di Pearson sono:

Il valore di 'r’ varia da '-1’ un '+1'. Il valore ‘0’ specifica che non esiste alcuna relazione tra le due variabili. Un valore maggiore di ‘0’ indica una relazione positiva tra due variabili in cui un aumento del valore di un variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... Aumenta il valore di un'altra variabile. Un valore inferiore a ‘0’ indica una relazione negativa tra due variabili dove un aumento del valore di una diminuisce il valore di un'altra variabile.

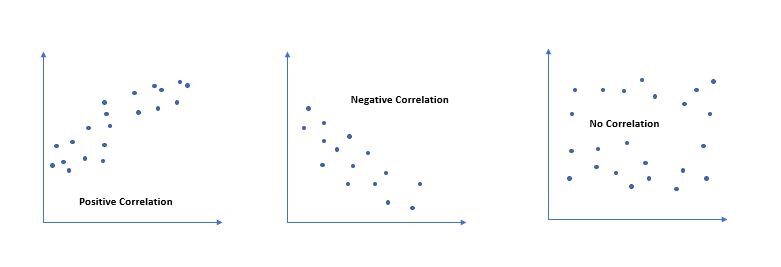
La correlazione di Pearson tenta di tracciare una linea di miglior adattamento attraverso la dispersione di due variabili. Perciò, specifica la distanza di tutti questi punti dati dalla linea di miglior adattamento. valore r’ uguale a circa +1 oh -1, il che significa che tutti i punti dati sono inclusi in corrispondenza o vicino alla linea di miglior adattamento, rispettivamente. Il valore di 'r’ più vicino ai punti dati ‘0’ è intorno alla linea della migliore vestibilità.

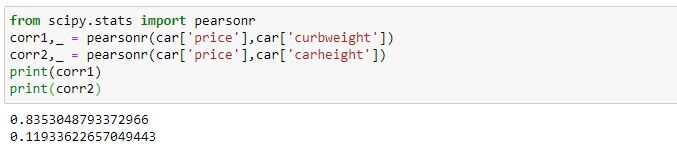
Considerando lo stesso esempio del prezzo dell'auto, Scopriamo il valore 'r’ utilizzando la "funzione di peersonr"’ e Python.

Come sopra, il valore della correlazione di Pearson per il prezzo rispetto al peso a vuoto è 0,835 e, in quanto non vi è alcuna correlazione tra il prezzo e l'altezza dell'auto, il valore della correlazione di Pearson tra il prezzo e l'altezza dell'auto è vicino a 0, Che cos'è 0,12.

Ipotesi per una correlazione di Pearson:

1. I dati devono essere derivati da campioni casuali o meno rappresentativi, trarre un'inferenza statistica significativa.

2. Entrambe le variabili devono essere continue e normalmente distribuite.

3. Ci deve essere omoschedasticità, il che significa che la variazione intorno alla linea di miglior adattamento dovrebbe essere simile.

4. I valori anomali estremi influenzano il coefficiente di correlazione di Pearson. Dovresti considerare valori anomali che sono insoliti in una sola variabile, denominada ‘variabile univariante’ o per entrambe le variabili note come "valori atipici multivariati". Guardami 2 variabili indipendentemente l'una dall'altra. Ad esempio, se riportiamo l'età in funzione dell'importo, poi, possiamo certamente vedere che c'è una correlazione tra l'età di una persona e il prestito, l'importo viene assegnato a quella persona, un misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... tale età aumenta l'importo del prestito concesso alla persona.

la persona diminuisce e viceversa. Ma se rappresentiamo l'importo del prestito in base all'età, non è possibile trarre alcuna conclusione. Violerebbe l'ipotesi.