Spiegazione chiara del raggruppamento gerarchico a collegamento singolo.

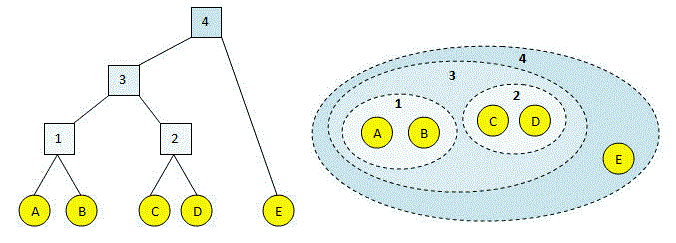
Come sappiamo tutti, Il raggruppamento gerarchico aggregato inizia con il trattamento di ogni osservazione come un singolo gruppo e quindi l'unione iterativa dei gruppi fino a quando tutti i punti dati vengono uniti in un singolo gruppo. Los dendrogramas se utilizan para representar resultados de raggruppamentoIl "raggruppamento" È un concetto che si riferisce all'organizzazione di elementi o individui in gruppi con caratteristiche o obiettivi comuni. Questo processo viene utilizzato in varie discipline, compresa la psicologia, Educazione e biologia, per facilitare l'analisi e la comprensione di comportamenti o fenomeni. In ambito educativo, ad esempio, Il raggruppamento può migliorare l'interazione e l'apprendimento tra gli studenti incoraggiando il lavoro.. jerárquico.

I cluster vengono uniti in base alla distanza tra loro e per calcolare la distanza tra i cluster abbiamo diversi tipi di link.

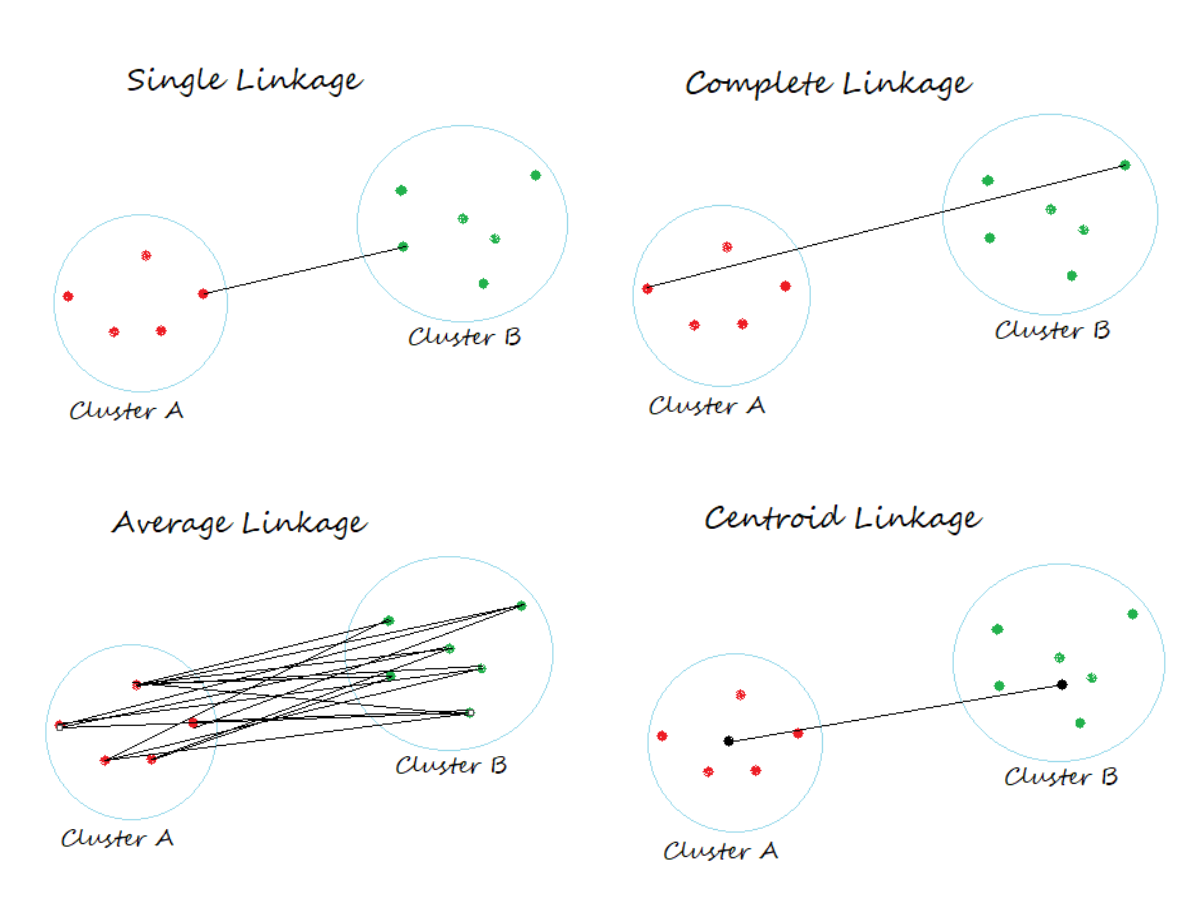
Criteri di collegamento:

Determinare la distanza tra insiemi di osservazioni in base alla distanza a coppie tra osservazioni.

• Sopra Collegamento singolo, la distanza tra due gruppi è la distanza minima tra i membri dei due gruppi
• Sopra Abbinamento completo, la distanza tra due gruppi è la distanza massima tra i membri dei due gruppi
• Sopra Collegamento medio, la distanza tra due cluster è la media di tutte le distanze tra i membri dei due cluster
• Sopra Collegamento centroide, la distanza tra due gruppi è la distanza tra i loro baricentri

In questo articolo, il nostro obiettivo è comprendere il processo di clustering utilizzando il metodo del collegamento singolo.

Raggruppamento a link singolo:

Inizia importando le librerie necessarie

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import scipy.cluster.hierarchy as shc
from scipy.spatial.distance import squareform, pdist

Creemos datos de juguetes usando numpy.random.random_sample

a = np.random.random_sample(dimensione = 5)
b = np.random.random_sample(dimensione = 5)

Una vez que generamos los puntos de datos aleatorios, crearemos un marco de datos de pandas.

point = ['P1','P2','P3','P4','P5']
data = pd.DataFrame({'Point':point, 'un':np.round(un,2), 'B':np.round(B,2)})
data = data.set_index('Point')
dati

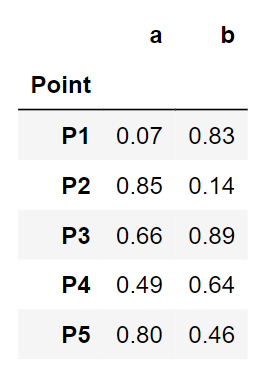
Uno sguardo ai dati dei nostri giocattoli. Sembra pulito. Passiamo ai passaggi di raggruppamento.

passo 1: visualice los datos usando un Diagramma di dispersioneIl grafico a dispersione è uno strumento grafico utilizzato in statistica per visualizzare la relazione tra due variabili. Consiste in un insieme di punti in un piano cartesiano, dove ogni punto rappresenta una coppia di valori corrispondenti alle variabili analizzate. Questo tipo di grafico consente di identificare i modelli, Tendenze e possibili correlazioni, facilitare l'interpretazione dei dati e il processo decisionale sulla base delle informazioni visive presentate....

plt.figure(figsize=(8,5))
plt.scatter(dati['un'], dati['B'], c="R", marcatore="*")
plt.xlabel('Colonna a')
plt.ylabel('colonna b')
plt.titolo('Grafico a dispersione di x e y')per j in data.ittuples():
    plt.annotate(j.Indice, (j.a, j.b), dimensione del carattere = 15)

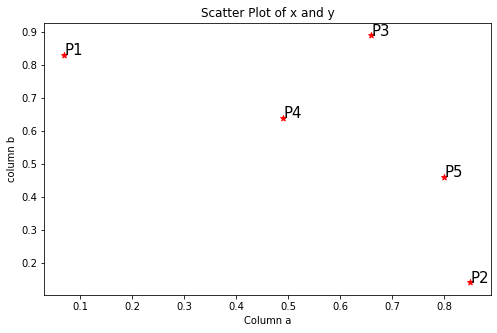
passo 2: calcolo della matrice delle distanze nel metodo euclideo usando pdist

dist = pd.DataFrame(forma quadrata(pdist(dati[['un', 'B']]), 'euclideo'), colonne=data.index.values, indice=dati.indice.valori)

Per nostra comodità, considereremo solo i valori del limite inferiore dell'array come mostrato di seguito.

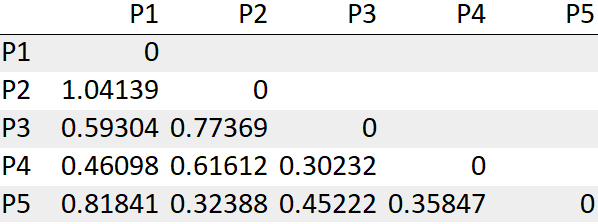
passo 3: trova la distanza più breve e combinali in un gruppo

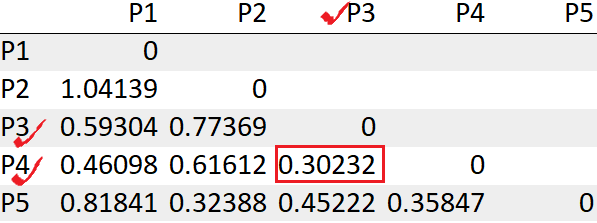
Vediamo i punti P3, P4 ha la distanza minima “0.30232”. Quindi, prima li uniremo in un gruppo.

passo 4: Ricalcola la matrice delle distanze dopo aver formato un gruppo

Aggiorna la distanza tra il gruppo (P3, P4) un P1

= Min (dist (P3, P4), P1)) -> min (dist (P3, P1), dist (P4, P1))

= Min (0.59304, 0.46098)

= 0,46098

Aggiorna la distanza tra il gruppo (P3, P4) un P2

= Min (dist (P3, P4), P2) -> min (dist (P3, P2), dist (P4, P2))

= Minimo (0,77369, 0,61612)

= 0,61612

Aggiorna la distanza tra il gruppo (P3, P4) un P5

= Min (dist (P3, P4), P5) -> min (dist (P3, P5), dist (P4, P5))

= Minimo (0.45222, 0.35847)

= 0.35847

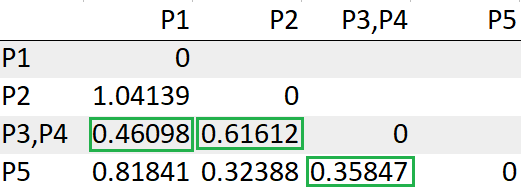
Ripeti i passaggi 3, 4 finché non restiamo con un solo gruppo.

Dopo aver ricalcolato la matrice delle distanze, debemos buscar nuevamente la distancia mínima para hacer un grappoloUn cluster è un insieme di aziende e organizzazioni interconnesse che operano nello stesso settore o area geografica, e che collaborano per migliorare la loro competitività. Questi raggruppamenti consentono la condivisione delle risorse, Conoscenze e tecnologie, promuovere l'innovazione e la crescita economica. I cluster possono coprire una varietà di settori, Dalla tecnologia all'agricoltura, e sono fondamentali per lo sviluppo regionale e la creazione di posti di lavoro.....

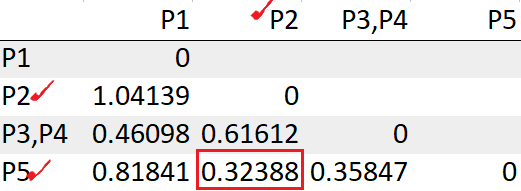
Vediamo i punti P2, P5 ha la distanza minima “0.32388”. Quindi li raggrupperemo in un gruppo e ricalcoleremo la matrice delle distanze.

Aggiorna la distanza tra il gruppo (P2, P5) un P1

= Min (dist ((P2, P5), P1)) -> min (dist (P2, P1), dist (P5, P1))

= Min (1.04139, 0.81841)

= 0,81841

Aggiorna la distanza tra il gruppo (P2, P5) un (P3, P4)

= Min (dist ((P2, P5), (P3, P4))) -> = Min (dist (P2, (P3, P4)), dist (P5, (P3, P4)))

= Min (dist (0.61612, 0.35847))

= 0.35847

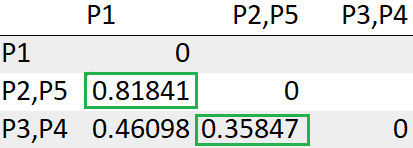
Dopo aver ricalcolato la matrice delle distanze, dobbiamo cercare ancora la distanza minima.

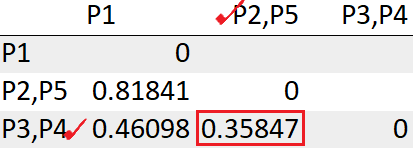
Il gruppo (P2, P5) ha la distanza minima dal gruppo (P3, P4) “0.35847”. Quindi li raggrupperemo insieme.

Aggiorna la distanza tra il gruppo (P3, P4, P2, P5) un P1

= Min (dist (((P3, P4), (P2, P5)), P1))

= Min (0,46098, 0,81841)

= 0,46098

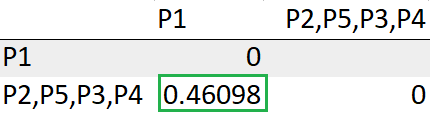
Con questo, finiamo per ottenere un singolo cluster.

Teoricamente, di seguito sono raggruppati i passaggi:

• Punti P3, P4 hanno la distanza più breve e sono fusi
• Punti P2, P5 hanno la distanza più breve e sono fusi
• I gruppi (P3, P4), (P2, P5) sono raggruppati
• Il gruppo (P3, P4, P2, P5) si fonde con il punto dati P1

Possiamo visualizzare lo stesso usando un dendrogramma.

plt.figure(figsize=(12,5)) 
plt.titolo("Dendrogramma con inchiostro singolo")  
dend = shc.dendrogram(shc.linkage(dati[['un', 'B']], metodo='singolo'), etichette=dati.indice)

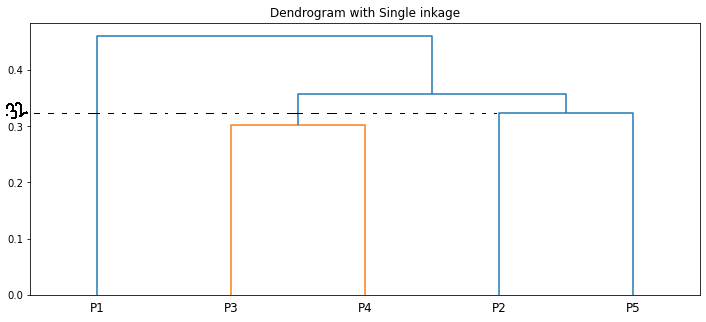
La lunghezza delle linee verticali nel dendrogramma mostra la distanza. Ad esempio, la distanza tra i punti P2, P5 è 0.32388.

Il raggruppamento passo passo che abbiamo fatto è lo stesso del dendrogramma🙌

Note finali:

Alla fine di questo articolo, abbiamo familiarità con il lavoro approfondito del raggruppamento gerarchico a collegamento singolo. Nel prossimo articolo, impareremo gli altri metodi di collegamento.

Riferimenti:

Raggruppamento gerarchico

Raggruppamento di link univoci

Collegamento al repository GitHub per pagare Jupyter Notebook

Spero che questo blog ti aiuti a capire come funziona il raggruppamento gerarchico a link singolo. Per favore, dagli una carezza 👏. Buon apprendimento !! ?

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato