Teoria della decisione bayesiana | Introduzione alla teoria della decisione bayesiana

Questo post è stato pubblicato come parte del Blogathon sulla scienza dei dati

introduzione

Teoria della decisione bayesiana si riferisce all'approccio statistico basato sulla quantificazione dei trade-off tra diverse decisioni di classificazione basate sul concetto di probabilità (Teorema di Bayes) e i costi associati alla decisione.

È semplicemente una tecnica di classificazione che prevede l'uso del teorema di Bayes che viene utilizzato per trovare le probabilità condizionate.

Sopra Accreditamento dei modelli statistici, ci concentreremo sulle proprietà statistiche dei pattern che sono generalmente espressi in densità di probabilità (pdf e pmf), e questo attirerà la maggior parte della nostra attenzione in questo post e cercheremo di sviluppare gli argomenti della teoria della decisione bayesiana.

Prerequisiti

VariabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... aleatoria

Una variabile casuale è una funzione che assegna un insieme ammissibile di risultati ad alcuni valori, come lanciare una moneta e ottenere il lato H come 1 e la coda a T come 0, dove 0 e 1 sono variabili casuali.

Teorema di Bayes

La probabilità condizionata di A dato B, rappresentato da P (UN | B) è la probabilità che si verifichi A dato che si è verificato B.

P (UN | B) = P (UN, B) / P (B) oh

Quando si utilizza la regola della catena, questo può anche essere scritto come:

P (UN, B) = P (UN | B) P (B) = P (B | UN) P (UN)

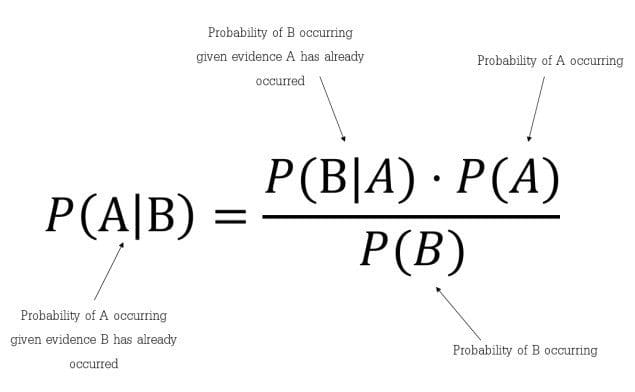
P (UN | B) = P (B | UN) P (UN) / P (B) ——- (1)

In cui si, P (B) = P (B, UN) + P (B, UN ') = P (B | UN) P (UN) + P (B | UN') P (UN ')

Qui, L'equazione (1) è conosciuto come Teorema di probabilità di Bayes

Il nostro obiettivo è esplorare ciascuno dei componenti inclusi in questo teorema. Esploriamo passo dopo passo:

(un) Precedente o Stato di Natura:

• Le probabilità a priori rappresentano la probabilità che ogni classe si verifichi.
• Quanto sopra è noto prima della procedura di formazione.
• Lo stato di natura è una variabile casuale P (w_io).
• Se ci sono solo due classi, allora la somma di quanto sopra è P (w₁) + P (w₂) = 1, se le lezioni sono esaurienti.

(B) Probabilità condizionali di classe:

• Rappresenta la probabilità della probabilità che si verifichi una caratteristica x dato che appartiene alla particolare classe. È indicato da, P (X | UN) dove x è una caratteristica particolare
• È la probabilità della probabilità che si verifichi la caratteristica x dato che appartiene alla classe w_io.
• Qualche volta, è anche conosciuto come Probabilità.
• È la quantità che dobbiamo esaminare durante l'addestramento dei dati. A lo largo del procedimiento de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina...., abbiamo l'ingresso (caratteristiche) X etichettato alla rispettiva classe w e calcoliamo la probabilità di occorrenza di quell'insieme di caratteristiche data l'etichetta della classe.

(C) Prova:

• È la probabilità che si verifichi una particolare caratteristica, In altre parole P (X).
• Può essere calcolato usando la regola della catena come, P (X) =_Su P (X | w_io) P (w_io)
• Come abbiamo bisogno della probabilità di probabilità condizionata di classe, inoltre, i valori delle prove sono calcolati durante l'allenamento.

(D) Probabilità a posteriori:

• È la probabilità che la classe A si verifichi quando si verificano determinate caratteristiche.
• È ciò che intendiamo calcolare nella fase di test in cui abbiamo input o caratteristiche di test (l'entità data) e dobbiamo scoprire quanto è probabile che il modello addestrato possa prevedere caratteristiche che appartengono alla particolare classe w_io.

Per una migliore comprensione della teoria di cui sopra, consideriamo un esempio

Descrizione del problema

Supponiamo di avere un'affermazione di un ostacolo di classificazione in cui dobbiamo categorizzare tra l'oggetto 1 e l'oggetto 2 con il dato insieme di caratteristiche. X = [X₁, X₂, …, X_n]^T.

obbiettivo

L'obiettivo principale della progettazione di un tale classificatore è suggerire azioni quando presentate con caratteristiche invisibili., In altre parole, un oggetto non ancora visto, In altre parole, non nei dati di allenamento.

In questo esempio, w denota lo stato di natura con w = w₁ per oggetto-1 e w = w₂ per oggetto-2. Qui, dobbiamo sapere che in realtà, lo stato di natura è così imprevedibile che in generale si considera che quello descritto probabilisticamente fosse variabile.

Priori

• In genere, assumiamo che ci sia qualche valore precedente P (w₁) che il prossimo oggetto è l'oggetto-1 e P (w₂) che l'oggetto successivo è l'oggetto-2. Se non abbiamo un altro oggetto come in questo problema, allora la somma dei suoi precedenti è 1, In altre parole, quanto sopra è esaustivo.
• Le probabilità a priori riflettono la conoscenza a priori della probabilità che otterremo l'oggetto 1 e l'oggetto 2. Dipende dal dominio, poiché il precedente può cambiare in base al periodo dell'anno in cui viene rilevato.

Sembra un po' strano e quando si giudicano più oggetti (come in uno scenario più realistico) rende stupida questa regola decisionale in quanto prendiamo sempre la stessa decisione in base al maggiore precedente anche se sappiamo che qualsiasi altro tipo di obiettivo potrebbe anche apparire governato dalle probabilità a priori in eccesso (poiché quanto sopra è di natura esaustiva).

Considera i seguenti diversi scenari:

• e P (?₁) >>> P (?₂), la nostra decisione a favore di ω₁ sarà corretto la maggior parte delle volte che prevediamo.
• Ma si P (?₁) = P (?₂), probabile mezzo della nostra previsione per essere corretto. Generalmente, la probabilità di errore è il minimo di P (?₁) y P (?₂), e più avanti in questo post, vedremo che in queste condizioni nessun'altra regola decisionale può produrre una maggiore probabilità di essere corretta.

Procedura di estrazione delle caratteristiche (Estrai funzionalità dalle immagini)

Una serie di funzionalità suggerite Lungo, larghezza, alternative per un oggettoeccetera.

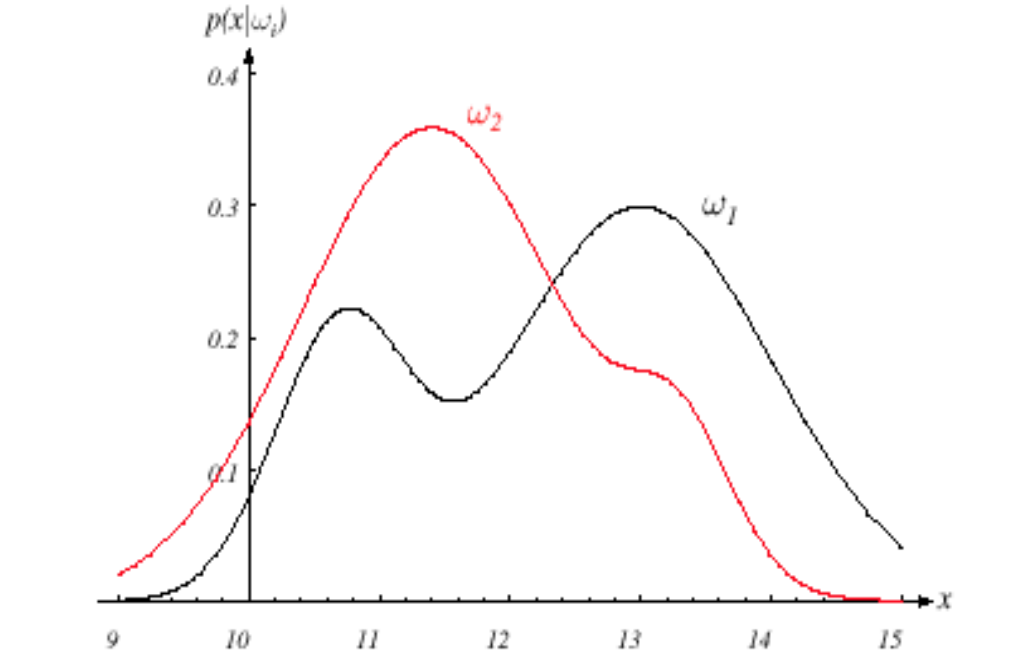
Nel nostro esempio, noi usiamo il larghezza x, Che è di più discriminatorio per guidare la regola decisionale del nostro classificatore. I diversi oggetti produrranno diverse letture di ampiezza variabile e in generale vediamo questa variabilità in termini probabilistici e consideriamo anche che x sia una variabile casuale continua la cui distribuzione dipende dal tipo di oggetto. w_J, ed è espresso come p (X | ?_J) (funzione di distribuzione di probabilità pdf come variabile continua) e nota come funzione di densità di probabilità condizionata di classe. Perché,

Il pdf p (X | ?₁) è la funzione di densità di probabilità per la caratteristica x dato che lo stato di natura è ω₁ e la stessa interpretazione per p (X | w₂).

Fig. Immagine che mostra pdf per entrambe le classi

Fonte immagine: Google Immagini

Supponiamo di conoscere bene le probabilità a priori P (?_J) e le densità condizionate p (X | ?_J). Ora, possiamo arrivare alla formula di Bayes per trovare le probabilità a posteriori:

Fig. Formula del teorema di Bayes

Fonte immagine: Google Immagini

La fórmula de Bayes nos da la intuición de que al observar la misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... de x podemos convertir la P (?_J) a dopo, indicato con P (?_J| X) che è la probabilità di_J poiché il valore caratteristico x è stato misurato.

P (X | ?_J) è nota come probabilità di_J rispetto all'ascia.

Il fattore evidenza, P (X), funziona semplicemente come un fattore di scala assicurando che le probabilità a posteriori si sommino a uno per tutte le classi.

Regola decisionale di Bayes

La regola decisionale date le probabilità a posteriori è la successiva

e P (w₁| X)> P (w₂| X) vorremmo decidere che l'oggetto appartiene alla classe w₁, o altrimenti classe w₂.

Probabilità di errore

Per giustificare la nostra decisione, esaminiamo la probabilità di errore, purché osserviamo x, avere,

P (errore | X) = P (w₁| X) se decidiamo w₂, e P (w₂| X) se decidiamo w₁

Come sono esaustivi e se scegliamo la natura corretta di un oggetto con probabilità P, quindi la rimanente probabilità (1-P) mostrerà quanto è probabile la decisione che non è l'oggetto deciso.

Possiamo minimizzare la probabilità di errore decidendo quale ha un posteriore maggiore e il resto poiché la probabilità di errore sarà la minima ammissibile. Quindi per finire otteniamo

P (errore | X) = min [P(?₁|X),P(?₂|X)]

E la nostra decisione di Bayes regola come,

Elegir₁ e P (?₁| X)> P (?₂| X); altrimenti decidi₂

Questo tipo di regola decisionale evidenzia il ruolo delle probabilità a posteriori. Con l'aiuto del teorema di Bayes, possiamo esprimere la regola in termini di probabilità a priori e condizionate.

Le prove sono irrilevanti per quanto riguarda la decisione. Come abbiamo già commentato, funziona semplicemente come un fattore di scala che indica la frequenza con cui misureremo la caratteristica con il valore x; assicura P (?₁| X) + P (?₂| X) = 1.

Quindi, eliminando il fattore di scala non richiesto nella nostra regola di decisione, abbiamo la regola di decisione simile del teorema di Bayes come,

Elegir₁ e P (X | ?₁) P (?₁)> p (X | ?₂) P (?₂); altrimenti decidi₂

Ora, consideriamo 2 casi:

• Caso 1: Se i condizionali di classe sono uguali, In altre parole, P (X | ?₁) = p (X | ?₂), arriviamo quindi alla nostra regola di decisione prematura governata solo a priori.
• Caso 2: D'altra parte, se quanto sopra è lo stesso, In altre parole, P (?₁) = P (?₂) allora la decisione si basa interamente su condizionali di classe p (X | ?_J).

Questo completa la nostra formulazione di esempio!!

Generalizzazione delle idee di cui sopra per più classi e caratteristiche

Classificazione di Bayes: posteriore, verosimiglianza, precedenti e prove

P (w_io | X) = P (X | w_io) P (w_io) / P (X)

Posteriore = Probabilità * Precedente / Prova

Ora discutiamo di quei casi che hanno caratteristiche multiple, così come più classi,

Lascia che siano più funzioni X₁, X₂, … X_Nord e più classi sono w₁, w₂,… W_Nord, dopo:

P (w_io | X₁,…. X_Nord) = P (X₁,…. , X_Nord| w_io) * P (w_io) / P (X₁,… X_Nord)

In cui si,

Posteriore = P (w_io | X₁,…. X_Nord)

Probabilità = P (X₁,…. , X_Nord| w_io)

Precedente = P (w_io)

Prova = P (X₁,… ,X_Nord)

In caso degli stessi modelli in entrata, potremmo aver bisogno di usare una funzione di costo drasticamente diversa, che porterà ad azioni assolutamente diverse. In genere, compiti decisionali diversi possono richiedere caratteristiche e limiti di prestazione molto diversi da quelli utili per il nostro problema di categorizzazione originale.

Quindi, nei post successivi, parleremo di Funzione di costo, Analisi del rischio, e azione decisiva che aiuterà a comprendere meglio la teoria delle decisioni di Bayes.

Note finali

Grazie per aver letto!

Se ti è piaciuto e vuoi saperne di più, visita gli altri miei post su data science e machine learning facendo clic su Collegamento

Sentiti libero di contattarmi a Linkedin, E-mail.

Tutto ciò che non è stato menzionato o vuoi condividere i tuoi pensieri? Sentiti libero di commentare qui sotto e ti ricontatterò.

Circa l'autore

Chirag Goyal

Oggi, Sto perseguendo il mio Bachelor of Technology (B.Tech) in informatica e ingegneria da Istituto indiano di tecnologia Jodhpur (IITJ). Sono molto entusiasta dell'apprendimento automatico, il apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute... y la inteligencia artificial.

Il supporto mostrato in questo post non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato