Analisi del componente principale | Guida all'analisi dei componenti principali

Sommario

• introduzione

• Panoramica fluida

• Contro dell'utilizzo di PCA

• Esempio pratico

• conclusione

introduzione

“L'intelligenza artificiale è l'ultima invenzione che l'umanità dovrà realizzare". La citazione chiarisce decisamente che l'apprendimento automatico è il futuro e grandi opportunità e vantaggi per tutti. Lascia che questo sia un nuovo inizio per imparare un algoritmo davvero interessante nell'apprendimento automatico.

Come tutti sanno, spesso ci imbattiamo nei problemi di archiviazione ed elaborazione dei big data nelle attività di apprendimento automatico, poiché è un processo che richiede tempo e sorgono difficoltà anche nell'interpretazione. Non tutte le funzionalità dei dati sono necessarie per le previsioni. Questi dati rumorosi possono portare a prestazioni scadenti e al sovradattamento del modello.. Attraverso questo articolo, lascia che ti presenti una tecnica di apprendimento senza supervisione PCA (Analisi del componente principale) che può aiutarti ad affrontare efficacemente questi problemi in una certa misura e fornire risultati di previsione più accurati.

La PCA è stata inventata all'inizio del XX secolo da Karl Pearson, analogo a teorema dell'asse principale in meccanica ed è ampiamente utilizzato. Attraverso questo metodo, trasformiamo effettivamente i dati in una nuova coordinata, dove quello con la varianza più alta è la componente principale principale. Fornendoci così la migliore rappresentazione possibile dei dati.

Morbido astratto

Dati con molte caratteristiche possono avere al loro interno correlazioni e duplicazioni. Quindi, una volta ottenuti i dati, il passaggio principale è pulirli rimuovendo le funzionalità irrilevanti e applicando tecniche di ingegneria delle funzionalità che possono persino fornire risultati migliori rispetto alle funzionalità originali. Analisi del componente principale (PCA) è una di quelle tecniche con cui è possibile la riduzione della dimensionalità (trasformazione lineare di attributi esistenti) e analisi multivariata. Ha diversi vantaggi, inclusa la riduzione delle dimensioni dei dati (così, esecuzione più veloce), visualizzazioni migliori con meno dimensioni, massimizzare la varianza, riduce il sovradattamento, eccetera.

Il componente principale significa in realtà le sequenze del vettore di direzione che differiscono in base alle linee di miglior adattamento. Si può anche affermare che queste componenti sono autovettori della matrice di covarianza. Esamineremo questo concetto di seguito..

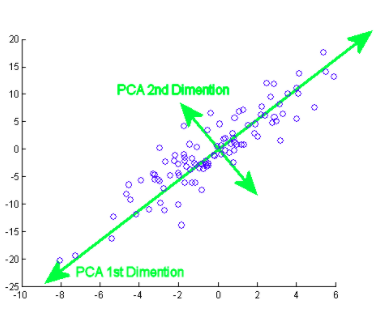
Come fai a fare questo? Inizialmente, necesitas encontrar los componentes principales desde diferentes puntos de vista durante la fase de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina...., da quelli che prendi le componenti importanti e meno correlate e ignori il resto, riducendo così la complessità. Il numero di componenti principali può essere inferiore o uguale al numero totale di attributi.

Supponiamo che due colonne X e Y siano le 2 caratteristiche,

XY

1 4

2 3

3 4

4 6

5 8

per significare

X ‘= 3, E’ = 5

Covarianza

il (X, e) = (Xi – X ') (Yi – E') / n – 1, dove io = 1 un

C = [ il(X,X) il (X,e) ]
[il(e,X) il(e,e) ]

Allo stesso modo, per ulteriori funzioni, troviamo la matrice di covarianza completa con più dimensioni. Continuando a calcolare gli autovalori, vettore, eccetera., possiamo trovare i componenti principali. L'importazione di algoritmi e l'utilizzo di librerie esatte semplifica l'identificazione dei componenti senza calcoli / operazioni manuali. Si noti che il numero di autovalori / Gli autovettori ti daranno il numero di dimensioni e la quantità di varianza associata a tali componenti.

però, poiché ci sono numerosi componenti principali dei big data, viene selezionato principalmente in base a quello che rappresenta la maggiore variazione possibile. Di conseguenza, anche le seguenti componenti vengono decise in ordine decrescente di varianza delle componenti precedenti ordinando gli autovalori, purché anche queste non abbiano una correlazione con le componenti principali precedenti. Quindi scartiamo quei componenti con meno autovalori / vettore (meno significativo).

Nell'ultimo passaggio, utilizziamo vettori di feature per orientare i dati verso quelli rappresentati dalle componenti principali (Analisi del componente principale). Questo viene fatto moltiplicando la trasposizione del set di dati originale per la trasposizione del vettore delle caratteristiche.

Contro dell'utilizzo di PCA / Svantaggi

Dovresti essere consapevole che la standardizzazione dei dati (che include anche la conversione di variabili categoriali in numeriche) è un must prima di usare PCA. Quando si applica PCA, le caratteristiche indipendenti diventano meno interpretabili perché anche questi componenti principali non sono leggibili o interpretabili. Ci sono anche possibilità che tu perda informazioni durante la PCA.

Esempio pratico

Ora, vediamo come viene implementato un algoritmo in un set di dati. Ti guiderò passo dopo passo attraverso ogni parte del codice.

Date un'occhiata al questo set di dati. Questo è il famoso set di dati sui fiori IRIS, contenenti caratteristiche come la lunghezza dei sepali, lunghezza del petalo, la larghezza del sepalo e la larghezza del petalo, y la variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... objetivo es la especie. Cosa intendi per variabile target è il valore / classe che devi prevedere, che in questo caso è il tipo di specie a cui appartiene il fiore.

fonte: Wikipedia

Importazione di set di dati e librerie di base

Primo, iniziamo importando le librerie necessarie,

importa numpy come np
importa panda come pd
importa matplotlib.pyplot come plt
da sklearn.datasets import load_iris

Carica i dati e visualizza i nomi delle caratteristiche e delle classi per la tua comprensione,

iris = load_iris()
#Nomi delle funzioni e codifica delle variabili di destinazione
Stampa(iris.feature_names)
Stampa(iris.target_names)
data = pd.DataFrame(iris.data)
data.columns = iris.feature_names
dati['CLASSE'] = iride.target
data.head()

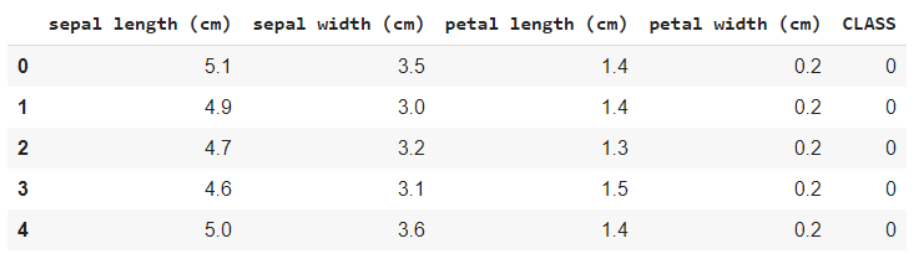
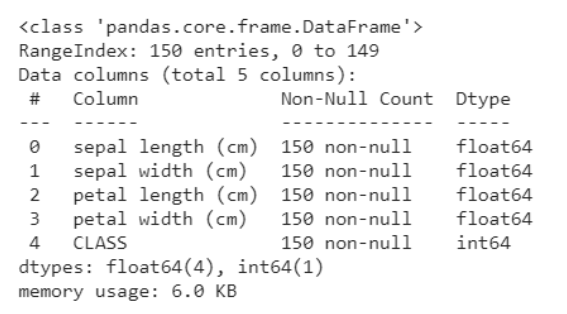
Il seguente frammento di codice ti aiuta a ottenere un'analisi dei dati, ovvero quante variabili sono categoriali e quante numeriche. Cosa c'è di più, è chiaro sotto che tutte le righe non sono nulle, in caso di oggetti nulli, otteniamo il conteggio e le righe / colonne in cui sono presenti. Questo ci aiuta a passare attraverso le fasi di pre-elaborazione per ripulire i dati.

data.info()

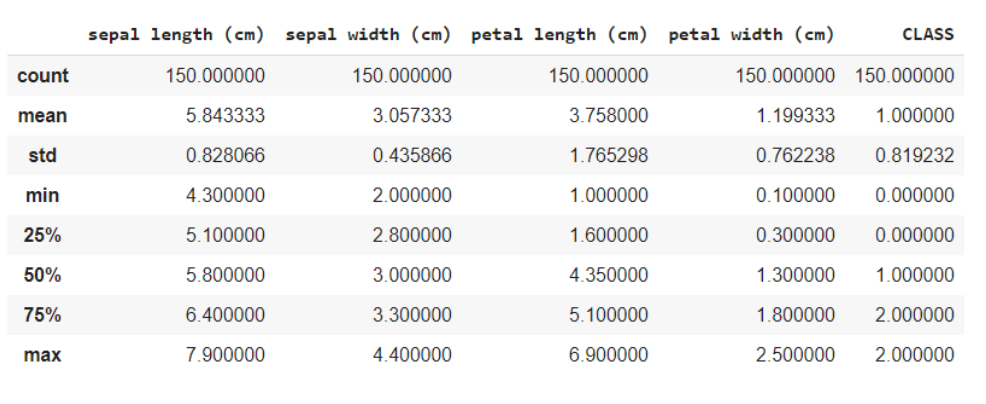
La funzione data.describe () fornisce generalmente una descrizione statistica del set di dati. Questi potrebbero essere utili in molti modi, puoi usare questi dati per riempire i valori mancanti o creare una nuova caratteristica, e molti altri.

dati.descrivi()

Qui stai dividendo i dati nelle caratteristiche e nelle variabili target come X e e rispettivamente. E quando si utilizza il metodo della forma, sa che i dati hanno 150 righe e 5 colonne in totale, di cui 1 la colonna è la tua variabile di destinazione e altre 4 sono le caratteristiche / attributi.

x = data.iloc[:,:4]  #caratteristiche
y = data.iloc[:,4] #obbiettivo
x.forma, y.forma

Fuori da: ((150, 4), (150,))

Poiché tutte le caratteristiche sono numeriche, è facile per il modello per l'allenamento. Se i dati contenevano variabili categoriali, dobbiamo prima convertirli in numerici, poiché le macchine / i computer possono gestire meglio i numeri.

Importazione libreria PCA

da sklearn.decomposition import PCA
pca = PCA()
X = pca.fit_transform(X)
pca.get_covariance()

spiegazione_varianza=pca.explained_variance_ratio_
spiegazione_varianza

Visualizzazioni

con plt.style.context('sfondo_scuro'):
    plt.figure(figsize=(6, 4))
    plt.bar(gamma(4), spiegazione_varianza, alfa=0,5, allinea='centro',
            etichetta="varianza spiegata individualmente")produzione
    plt.ylabel('Rapporto di varianza spiegato')
    plt.xlabel("Componenti principali")
    plt.legend(loc ="migliore")
    plt.tight_layout()

Dalle visualizzazioni si ricava l'intuizione che ci sono principalmente solo 3 componenti con varianza significativa, così, selezioniamo il numero di componenti principali come 3.

pca = PCA(n_components=3)
X = pca.fit_transform(X)

Test del treno diviso

La divisione del test del treno è un metodo comune di formazione e valutazione. Generalmente, le previsioni sugli stessi dati addestrati possono portare a sovradattamento, dando così cattivi risultati per dati sconosciuti. In questo caso, dividendo i dati in training set e test set, ti alleni e poi prevedi usando il modello in 2 diversi set, risolvendo così il problema del sovradattamento.

da sklearn.model_selection import train_test_split
X_treno, X_test, y_train, y_test = train_test_split(X, e, test_size = 0.3, stato_casuale=20, stratificare=y)

Formazione modello

Il nostro obiettivo è identificare la classe / specie a cui il fiore appartiene date alcune sue caratteristiche. Perciò, questo è un problema di classificazione e il modello che usiamo usa K vicini più prossimi.

da sklearn.neighbors import KNeighborsClassifier
modello = KNeighborsClassifier(7)
model.fit(X_treno,y_train)
y_pred = model.predict(X_test)

Predizioni

da sklearn.metrics import confusione_matrix
da sklearn.metrics import precision_score
cm = confusione_matrice(y_test, y_pred)  #confusione_matrice
Stampa(cm)
Stampa(precision_score(y_test, y_pred))

La matrice di confusione ti mostrerà il conteggio dei falsi positivi, falsi negativi, veri positivi e veri negativi.

La puntuación de precisión le indicará en qué misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... nuestro modelo ha sido eficaz a la hora de ofrecer predicciones para nuevos datos. Il 97% è un ottimo punteggio, ed è per questo che possiamo dire che il nostro è un buon modello.

Puoi vedere il codice completo su questa collaborazione google previsto.

conclusione

Spero davvero che tu abbia avuto un'intuizione sulla PCA e che tu abbia familiarità con l'esempio discusso sopra. Non è così complesso da digerire, resta concentrato. Assicurati di leggerlo ancora una volta se lo trovi utile e sviluppa tu stesso l'algoritmo per capirlo meglio..

Buona giornata !! ?

Imparentato