Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Regressione lineare:
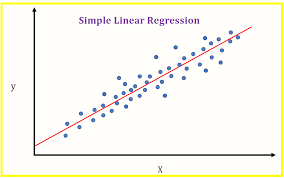
Figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... 1.0: Visualizzazione del modello di regressione lineare di base
Il modello lineare (regressione lineare) è stato probabilmente il primo modello che ha imparato e creato, utilizzo del modello per prevedere valori target continui. Sicuramente devi essere stato felice di aver completato un modello. Probabilmente ti hanno anche insegnato le teorie dietro la sua funzionalità: minimizzazione empirica del rischio, perdita media al quadrato, el descenso del gradienteGradiente è un termine usato in vari campi, come la matematica e l'informatica, per descrivere una variazione continua di valori. In matematica, si riferisce al tasso di variazione di una funzione, mentre in progettazione grafica, Si applica alla transizione del colore. Questo concetto è essenziale per comprendere fenomeni come l'ottimizzazione negli algoritmi e la rappresentazione visiva dei dati, consentendo una migliore interpretazione e analisi in..., il tasso di apprendimento, tra l'altro.
Bene, è fantastico e all'improvviso sono stato chiamato per spiegare un modello che ho creato al manager, tutti quei termini erano come uno slang per lui, e quando hai chiesto di vedere il modello (come in figura 1.0) questo è il modello adatto all'iperpiano (la linea rossa) e i punti dati (i puntini blu). Mi sono bloccato fino ai piedi non sapendo come crearlo nel codice Python.
Bene, questo è ciò che riguarda la prima parte di questo articolo sulla creazione della visualizzazione del modello lineare di base nel tuo notebook Jupyter in Python.
Iniziamo a utilizzare questi dati casuali:
| X | e |
| 1 | 2 |
| 2 | 3 |
| 3 | 11 |
| 4 | 13 |
| 5 | 28 |
| 6 | 32 |
| 7 | 50 |
| 8 | 59 |
| 9 | 85 |
Metodo 1: Formulazione manuale
Importazione della nostra libreria e creazione del frame di dati:

Ora, in questa fase, ci sono due modi per fare questa visualizzazione:
1.) Usa le conoscenze matematiche
2.) L'utilizzo dell'attributo Linear_regression per scikit apprende Linear_model.
- Iniziamo con la matematica😥😥.
vai avanti, non è così difficile, definiamo prima l'equazione per una relazione lineare tra e (variabili dipendenti / obbiettivo) e X (variabile indipendente / caratteristiche) Che cosa:
y = mX + C
dove y = obiettivo
X = caratteristiche
a = pendenza
b = costante dell'intercetta y
Per creare l'equazione del modello dobbiamo ottenere il valore di myc, possiamo ottenere questo da Y e X con le seguenti equazioni:
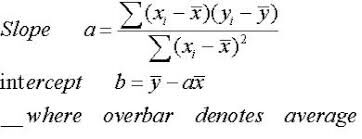
Pendenza, a è interpretato come il Prodotto tra la somma della differenza tra ogni singolo valore x e la sua media y TLa somma della differenza tra ogni punto e individuo e la sua media dopo Diviso di la somma dei quadrati di ogni individuo x e la sua media.
L'intersezione è semplicemente il media di y meno il prodotto della pendenza e la media di x
È molto da accettare. Probabilmente lo leggerai più e più volte finché non lo capisci, prova a leggere con l'immagine
👆👆 quella era l'unica sfida; Se hai capito, congratulazioni, andiamo avanti.
Ora scrivere questo nel codice Python è 'eazy-pizzy’ usando la biblioteca numpy, controllalo.
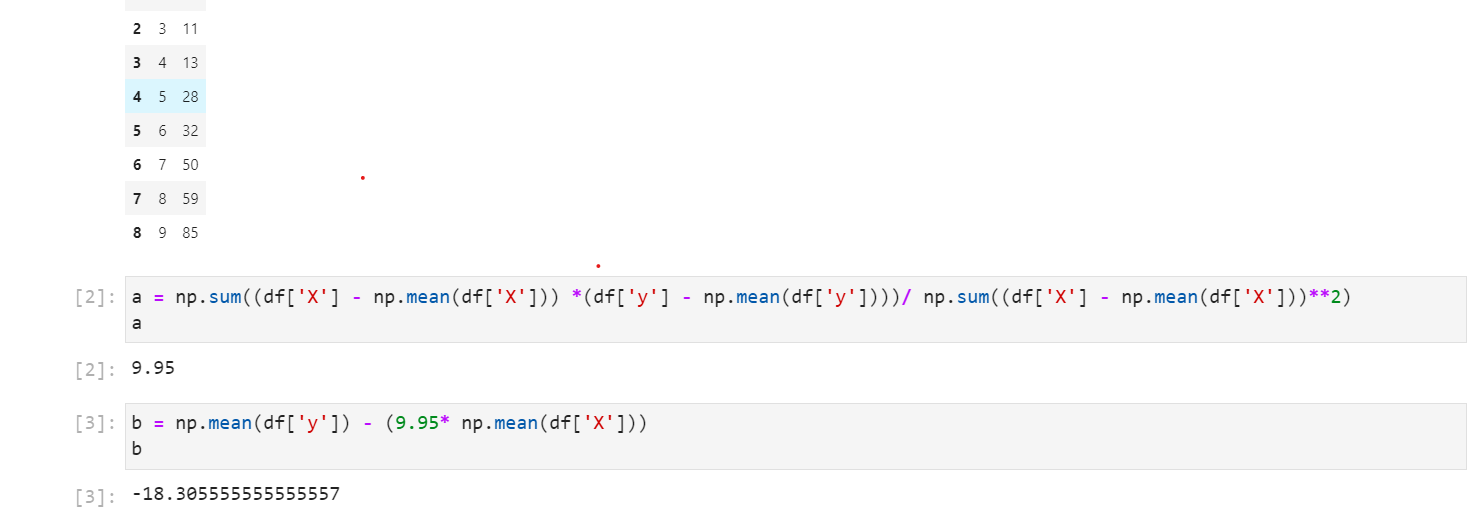
ora abbiamo i nostri a e b, lo inseriamo semplicemente nell'equazione —-> y = 9,95 -1218,56X
Per farti impazzire adesso, Lo sapevi che questa è l'equazione del modello?? e abbiamo appena creato un modello senza usare scikit learn. Lo confermeremo ora usando il secondo metodo che è il pacchetto scikit learn Linear Regression
Metodo 2: usa la regressione lineare scikit-learn
Wnoi saremo importazione di regressione lineare da scikit learn, adatta i dati nel modello e quindi conferma la pendenza e l'intercetta. I passaggi sono nell'immagine qui sotto.
quindi puoi vedere che non c'è quasi nessuna differenza, ora visualizziamolo come in figura 1.

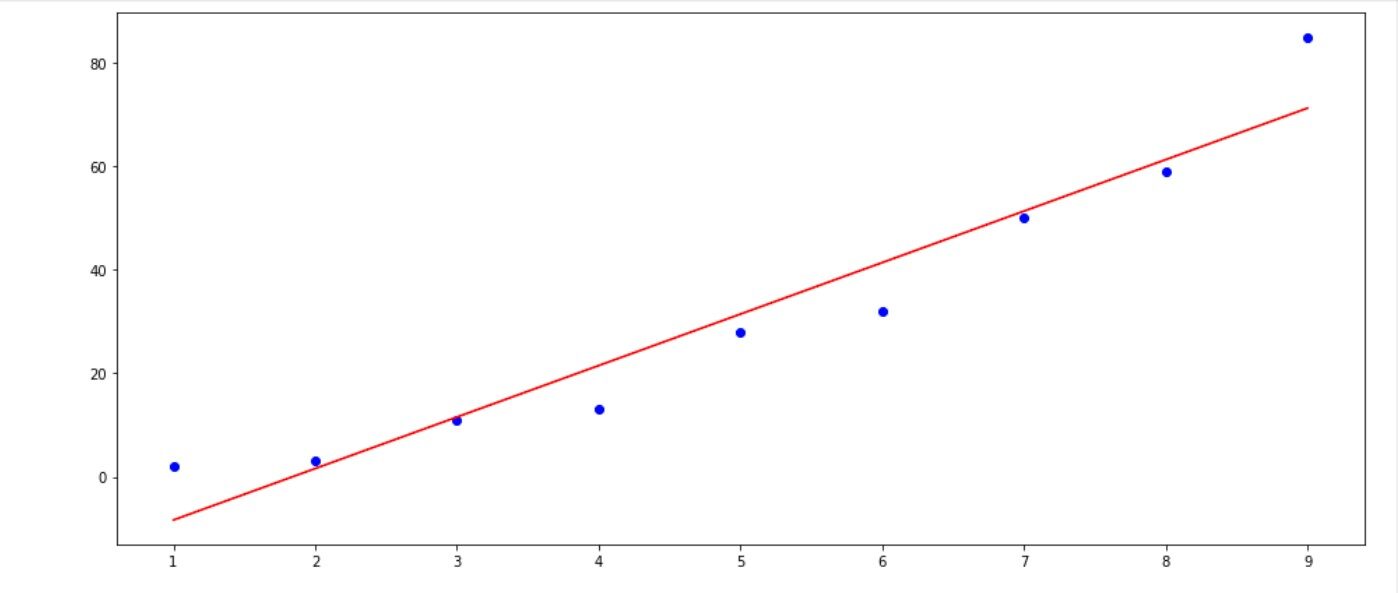
La linea rossa è la nostra linea più adatta da utilizzare per la previsione e il punto blu è il nostro dato iniziale. Con questo, aveva qualcosa da riferire al manager. L'ho fatto in particolare per ogni funzione con l'obiettivo di aggiungere più informazioni.
Ora abbiamo raggiunto il nostro obiettivo di creare un modello e visualizzare il suo grafico tracciato.
Questa tecnica può richiedere molto tempo quando si tratta di dati di dimensioni maggiori e dovrebbe essere utilizzata solo quando si visualizza la linea più adatta con una particolare caratteristica a scopo di analisi.. Non proprio necessario durante la modellazione se non richiesto. Errori e calcoli possono consumare tempo e risorse di calcolo, soprattutto se stai lavorando con dati 3D e superiori. Ma le informazioni ottenute ne valgono la pena.
Spero che l'articolo ti sia piaciuto, si è così bello, puoi anche dirmi come migliorare in qualche modo. Ho ancora molto da condividere, soprattutto sulle regressioni (lineare, logistico e polinomiale).
Grazie per aver letto.
Imparentato
Articoli correlati:
- Modellazione predittiva in Excel | Come creare un modello di regressione lineare
- Regressione lineare | Introduzione alla regressione lineare per la scienza dei dati
- Regressione lineare e logistica | Regressione lineare e logistica
- Regressione lineare | Prevedere utilizzando la regressione lineare in R






