Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Un metodo statistico popolare e ampiamente utilizzato per la previsione delle serie temporali è il modello ARIMA.. Il livellamento esponenziale e i modelli ARIMA sono i due approcci più utilizzati per la previsione delle serie temporali e forniscono approcci complementari al problema.. Mentre i modelli di livellamento esponenziale si basano su una descrizione dell'andamento e della stagionalità dei dati, I modelli ARIMA mirano a descrivere le autocorrelazioni nei dati.
Per conoscere la stagionalità, controlla questo blog.
Prima di parlare del modello ARIMA, parliamo del concetto di stazionarietà e della tecnica di differenziazione delle serie temporali.
stazionarietà
I dati di una serie temporale stazionaria sono quelli le cui proprietà non dipendono dal tempo, da qui la serie storica con le tendenze, o con la stagionalità, non sono stazionari. la tendenza e la stagionalità influenzeranno il valore della serie temporale in momenti diversi. In secondo luogo, per la stazionarietà non importa quando la guardi, dovrebbe essere molto simile in qualsiasi momento. Generalmente, una serie storica stazionaria non avrà modelli prevedibili a lungo termine.
ARIMA è l'acronimo di Auto-Regressive Integrated Moving Average. È una classe modello che cattura un insieme di diverse strutture temporali standard nei dati delle serie temporali.
In questo tutorial, parleremo di come sviluppare un modello ARIMA per la previsione delle serie temporali in Python.
Un modello ARIMA è una classe di modelli statistici per l'analisi e la previsione dei dati delle serie temporali. È davvero semplificato in termini di utilizzo. tuttavia, questo modello è davvero potente.
ARIMA sta per Media Mobile Integrata Auto-regressiva.
I parametri del modello ARIMA sono definiti come segue:
P: Il numero di osservazioni di ritardo incluse nel modello, chiamato anche ordine di ritardo.
D: Il numero di volte in cui le osservazioni grezze differiscono, chiamato anche grado di differenza.
Q: La dimensione della finestra della media mobile, chiamato anche ordine a media mobile.
Viene costruito un modello di regressione lineare che include il numero e il tipo di termini specificati, e i dati sono preparati da un grado di differenziazione per renderli stazionari, vale a dire, eliminare le strutture di tendenza e stagionali che influiscono negativamente sul modello di regressione.
PASSI
1. Visualizzare i dati delle serie temporali
2. Identificare se la data è stazionaria
3. Tracciare i grafici di correlazione e correlazione automatica
4. Creare il modello ARIMA o ARIMA stagionale in base ai dati
Cominciamo
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
In questo tutorial, Sto usando il seguente set di dati.
df=pd.read_csv('time_series_data.csv')
df.head()
# Updating the header
df.columns=["Mese","Saldi"]
df.head()
df.descrivi()
df.set_index('Mese',inplace=Vero)
from pylab import rcParams
rcParams['figura.figsize'] = 15, 7
df.plot()
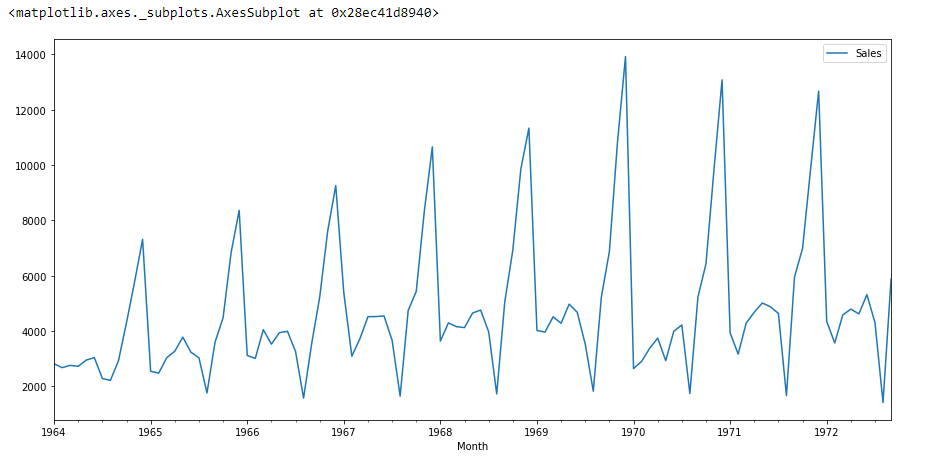
Se vediamo il grafico precedente, possiamo trovare una tendenza che c'è un momento in cui le vendite sono alte e viceversa. Ciò significa che possiamo vedere che i dati seguono la stagionalità.. ad ARIMA, la prima cosa che facciamo è identificare se i dati sono stazionari o non stazionari. se i dati non sono stazionari, proveremo a renderli stazionari e poi ad elaborarne altri.
Verifichiamo che se il dato set di dati è stazionario o meno, per questo usiamo adfuller.
da statsmodels.tsa.stattools import adfuller
Ho importato l'adfuller eseguendo il codice sopra.
test_result=adfuller(df['Saldi'])
Per identificare la natura dei dati, useremo l'ipotesi nulla.
H0: L'ipotesi nulla: È un'affermazione sulla popolazione che si crede sia vera o usata per fare un'argomentazione a meno che non si possa dimostrare che è errata oltre ogni ragionevole dubbio.
H1: L'ipotesi alternativa: È un'affermazione sulla popolazione che contraddice h0 e cosa concludiamo quando rifiutiamo h0.
#come: non è stazionario
# H1: è fermato
Considereremo l'ipotesi nulla che i dati non siano stazionari e l'ipotesi alternativa che i dati siano stazionari.
def adfuller_test(saldi):
risultato=adfuller(saldi)
etichette = ["Statistiche test ADF",'valore p','#Lag utilizzati',"Numero di osservazioni"]
per valore,etichetta in zip(risultato,etichette):
Stampa(etichetta+' : '+str(valore) )
se risultato[1] <= 0.05:
Stampa("forti prove contro l'ipotesi nulla(come), rifiutare l'ipotesi nulla. I dati sono stazionari")
altro:
Stampa("prove deboli contro l'ipotesi nulla,indicando che non è stazionario ")
adfuller_test(df['Saldi'])
Dopo aver eseguito il codice precedente otterremo il valore P,
Statistica test ADF : -1.8335930563276237 valore p : 0.3639157716602447 #Ritardi utilizzati : 11 Numero di osservazioni : 93
Qui il valore di P è 0.36, che è maggiore di 0.05, il che significa che i dati accettano l'ipotesi nulla, il che significa che i dati non sono stazionari.
Proviamo a vedere la prima differenza e la differenza stagionale:
df['Vendite prima differenza'] = df['Saldi'] - df['Saldi'].spostare(1) df["Prima differenza stagionale"]=df['Saldi']-df['Saldi'].spostare(12) df.head()
# Again testing if data is stationary
adfuller_test(df["Prima differenza stagionale"].gocciolare())
Statistica test ADF : -7.626619157213163
valore p : 2.060579696813685e-11
#Lags Used : 0
Numero di osservazioni : 92
Qui il valore di P è 2.06, il che significa che rifiuteremo l'ipotesi nulla. Entonces los datos son estacionarios.
df["Prima differenza stagionale"].complotto()
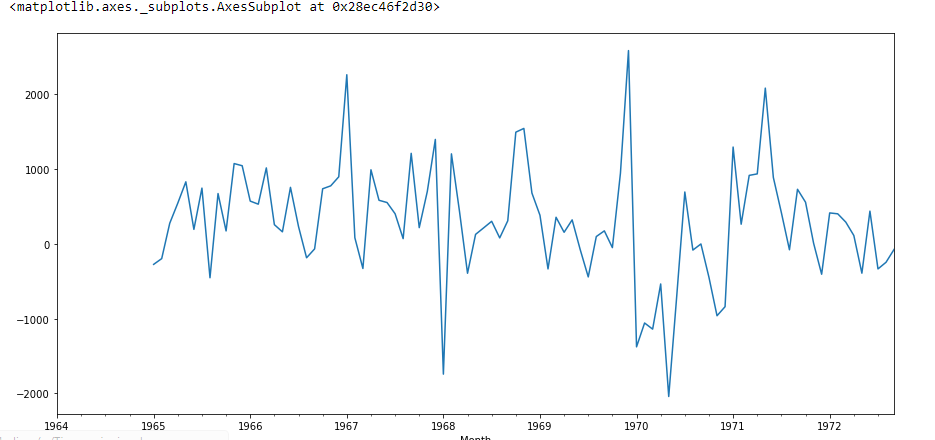
Voy a crear autocorrelación:
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(df['Saldi'])
plt.mostra()
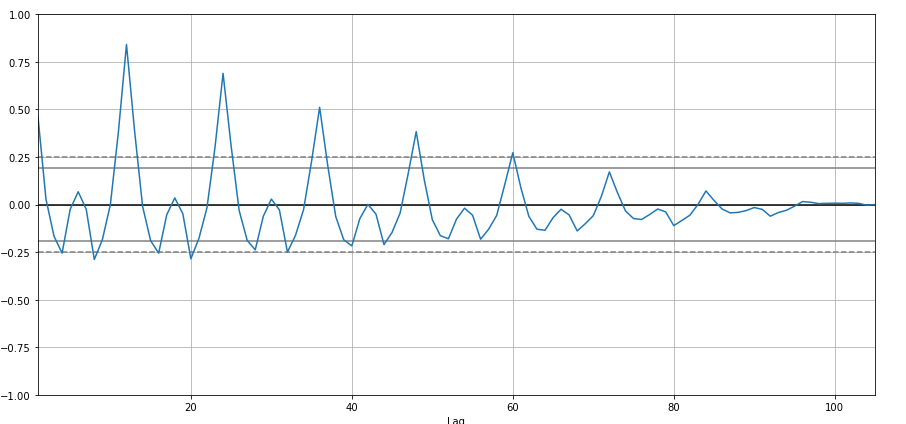
da statsmodels.graphics.tsaplots importare plot_acf,plot_pacf
import statsmodels.api as sm
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fico = sm.graphics.tsa.plot_acf(df["Prima differenza stagionale"].gocciolare(),lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fico = sm.graphics.tsa.plot_pacf(df["Prima differenza stagionale"].gocciolare(),lags=40,ax=ax2)
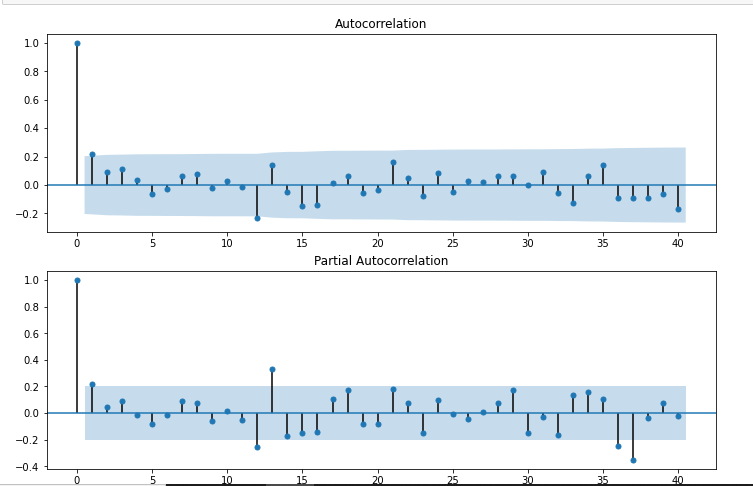
# For non-seasonal data #p=1, d=1, q=0 o 1 from statsmodels.tsa.arima_model import ARIMA model=ARIMA(df['Saldi'],ordine=(1,1,1)) model_fit=model.fit() model_fit.sommario()
| Dep. Variabile: | D. Saldi | No. Osservazioni: | 104 |
|---|---|---|---|
| Modello: | ARIMA (1, 1, 1) | Probabilidad logarítmica | -951.126 |
| Metodo: | css-mle | SD de innovaciones | 2227.262 |
| Data: | Mié ·, 28 ott 2020 | AIC | 1910.251 |
| Tempo metereologico: | 11:49:08 | BIC | 1920.829 |
| Spettacoli: | 02-01-1964 | HQIC | 1914.536 |
| – 09-01-1972 |
| coef | std err | Insieme a | P> | Insieme a | | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| costante | 22.7845 | 12.405 | 1.837 | 0.066 | -1.529 | 47.098 |
| Ar. L1. D.Vendite | 0.4343 | 0,089 | 4.866 | 0.000 | 0,259 | 0,609 |
| mamma. L1. D.Vendite | -1,0000 | 0,026 | -38.503 | 0.000 | -1.051 | -0,949 |
| Vero | Imaginario | R Marketing e i suoi istruttori accreditati forniscono formazione faccia a faccia in Australia e formazione dal vivo e unica in tutto il mondo | Frequenza | |
|---|---|---|---|---|
| AR.1 · | 2.3023 | + 0,0000J | 2.3023 | 0,0000 |
| MA.1 · | 1,0000 | + 0,0000J | 1,0000 | 0,0000 |
df['previsione']=model_fit.predict(start=90,end=103,dynamic=True) df[['Saldi','previsione']].complotto(figsize=(12,8))
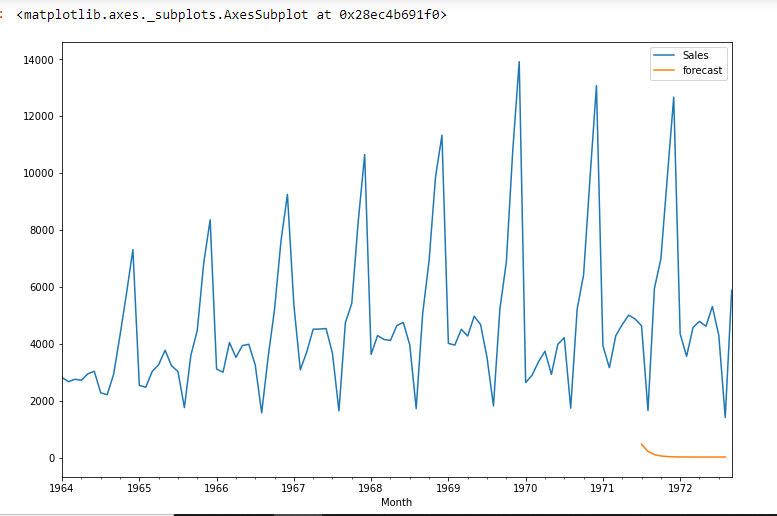
import statsmodels.api as sm
model=sm.tsa.statespace.SARIMAX(df['Saldi'],ordine=(1, 1, 1),seasonal_order=(1,1,1,12))
risultati=model.fit()
df['previsione']=risultati.prevedere(start=90,end=103,dynamic=True)
df[['Saldi','previsione']].complotto(figsize=(12,8))
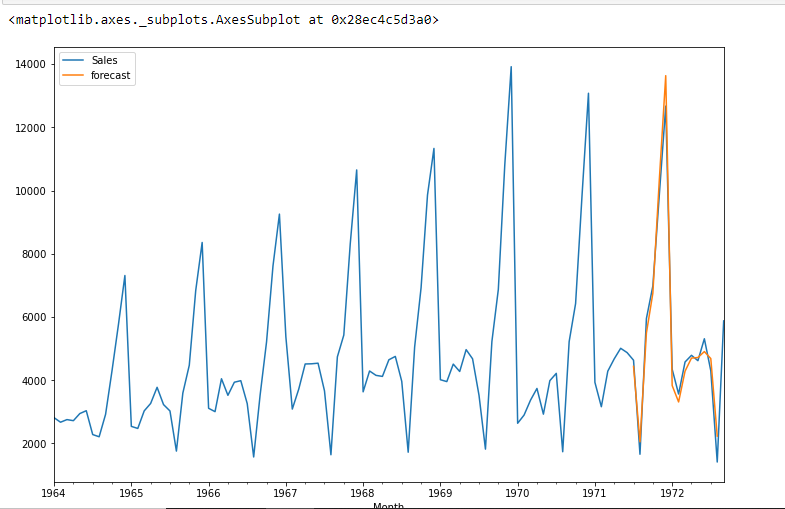
from pandas.tseries.offsets import DateOffset
future_dates=[df.index[-1]+ DataOffset(mesi=x)per x nell'intervallo(0,24)]
future_datest_df=pd. DataFrame(indice=future_dates[1:],colonne=df.columns)
future_datest_df.tail()
future_df=pd.concat([df,future_datest_df])
future_df['previsione'] = risultati.prevedere(inizio = 104, fine = 120, dynamic= Vero)
future_df[['Saldi', 'previsione']].complotto(figsize=(12, 8))
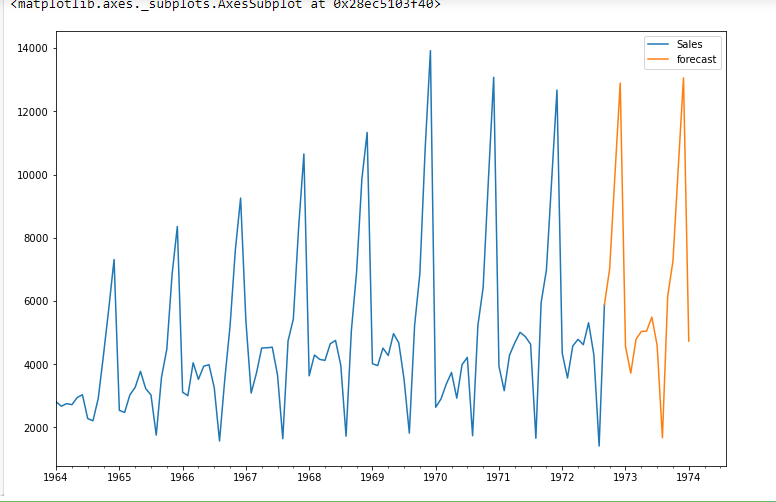
conclusione
La previsione delle serie temporali è davvero utile quando dobbiamo prendere decisioni future o dobbiamo fare analisi, possiamo farlo rapidamente usando ARIMA, ci sono molti altri modelli da cui possiamo fare previsioni di serie temporali, ma ARIMA è davvero facile da capire.
Spero che questo articolo ti aiuti e ti faccia risparmiare una buona quantità di tempo.. Fatemi sapere se avete suggerimenti..
FELICE CODIFICA.
Prabhat Pathak (Profilo LinkedIn) es analista senior.
