Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Il clustering è una tecnica di apprendimento automatico senza supervisione. È il processo di divisione del set di dati in gruppi in cui i membri dello stesso gruppo hanno caratteristiche simili.. Gli algoritmi di clustering più comunemente usati sono il clustering K-means, raggruppamento gerarchico, pooling basato sulla densità, clustering basato su modelli, eccetera. In questo articolo, vamos a discutir el raggruppamentoIl "raggruppamento" È un concetto che si riferisce all'organizzazione di elementi o individui in gruppi con caratteristiche o obiettivi comuni. Questo processo viene utilizzato in varie discipline, compresa la psicologia, Educazione e biologia, per facilitare l'analisi e la comprensione di comportamenti o fenomeni. In ambito educativo, ad esempio, Il raggruppamento può migliorare l'interazione e l'apprendimento tra gli studenti incoraggiando il lavoro.. de K-Means en detalle.
Raggruppamento di K-calze
Es el algoritmo de Apprendimento non supervisionatoL'apprendimento non supervisionato è una tecnica di apprendimento automatico che consente ai modelli di identificare modelli e strutture nei dati senza etichette predefinite. Attraverso algoritmi come k-means e analisi delle componenti principali, Questo approccio viene utilizzato in una varietà di applicazioni, come la segmentazione dei clienti, Rilevamento delle anomalie e compressione dei dati. La sua capacità di rivelare informazioni nascoste lo rende uno strumento prezioso... de tipo iterativo más simple y de uso común. In questo, Inizializziamo in modo casuale il K numero di centroidi nei dati (il numero di k si trova usando il Gomito metodo che sarà discusso più avanti in questo articolo) e iterare questi centroidi fino a quando non si verifica alcun cambiamento nella posizione del centroide. Esaminiamo i passaggi coinvolti in K significa raggruppare per una migliore comprensione.
1) Seleziona il numero di cluster per il set di dati (K)
2) Seleziona K numero di centroidi
3) Quando si calcola la distanza euclidea o la distanza di Manhattan, assegnare punti a baricentro più vicino, creando così gruppi K
4) Ora trova il baricentro originale in ciascun gruppo
5) Rimappa nuovamente l'intero punto dati in base a questo nuovo centroide, quindi ripetere il passaggio 4 finché la posizione del baricentro non cambia.
Trovare il numero ottimale di cluster è una parte importante di questo algoritmo.. Un metodo comunemente usato per trovare il valore ottimale di K è Metodo del gomito.
Metodo del gomito
Nel metodo del gomito, stiamo effettivamente variando il numero di cluster (K) a partire dal 1 un 10. Per ogni valore di K, stiamo calcolando WCSS (Somma del quadrato all'interno del cluster). WCSS è la somma della distanza al quadrato tra ciascun punto e il baricentro in un gruppo. Quando tracciamo il WCSS con il valore K, il grafico sembra un gomito. All'aumentare del numero di cluster, il valore WCSS inizierà a diminuire. Il valore WCSS è maggiore quando K = 1. Quando osserviamo il grafico, possiamo vedere che il grafico cambierà rapidamente in un punto e, così, creerà una forma a gomito. Da questo punto, il grafico inizia a muoversi quasi parallelamente all'asse X. Il valore K corrispondente a questo punto è il valore K ottimale o un numero ottimale di cluster.
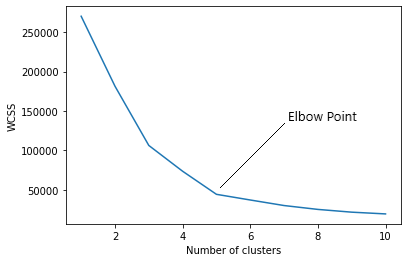
Ora implementiamo il clustering K-Means usando Python.
Implementazione
Primo, dobbiamo importare le librerie essenziali.
importa numpy come np importa matplotlib.pyplot come plt importa panda come pd importa sklearn
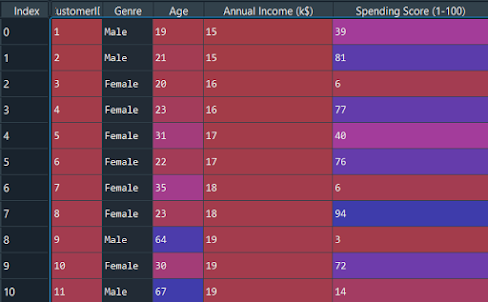
Ora importiamo il set di dati e separiamo le funzionalità importanti.
set di dati = pd.read_csv('Clienti_centro commerciale.csv') X = dataset.iloc[:, [3, 4]].valori
Dobbiamo trovare il valore ottimale di K per raggruppare i dati. Ora stiamo usando il metodo del gomito per trovare il valore ottimale di K.
da sklearn.cluster importa KMeans wcss = [] per io nel raggio d'azione(1, 11): kmsignifica = KMezzi(n_cluster = i, inizia="k-significa++", stato_casuale = 42) kmeans.fit(X) wcss.append(kmeans.inerzia_)
L'argomento “dentro” è il metodo per inizializzare il baricentro. Calcoliamo il valore WCSS per ogni valore K. Ora dobbiamo tracciare il WCSS con valore K
plt.trama(gamma(1, 11), wcss) plt.xlabel('Numero di cluster') plt.ylabel('WCSS') plt.mostra(
Il grafico sarà-
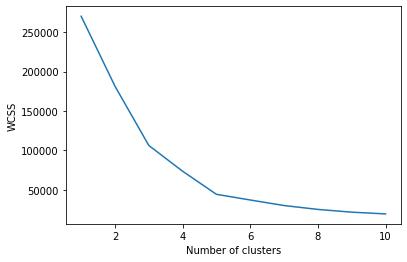
Il punto in cui viene creata la forma del gomito è 5, vale a dire, il nostro valore K o un numero ottimale di cluster è 5. Ora addestriamo il modello sul set di dati con un numero di cluster 5.
kmsignifica = KMezzi(n_cluster = 5, inizia = "k-significa++", stato_casuale = 42) y_kmeans = kmeans.fit_predict(X)
y_kmeans sarà:
Vettore([3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0,
3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 1,
3, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 2, 1, 2, 4, 2, 4, 2,
1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2])plt.scatter(X[y_ksignifica == 0, 0], X[y_ksignifica == 0, 1], s = 60, c="rosso", etichetta="Cluster1") plt.scatter(X[y_ksignifica == 1, 0], X[y_ksignifica == 1, 1], s = 60, c="blu", etichetta="Cluster2") plt.scatter(X[y_ksignifica == 2, 0], X[y_ksignifica == 2, 1], s = 60, c="verde", etichetta="Cluster3) plt.scatter(X[y_ksignifica == 3, 0], X[y_ksignifica == 3, 1], s = 60, c = "Viola', etichetta="Cluster4") plt.scatter(X[y_ksignifica == 4, 0], X[y_ksignifica == 4, 1], s = 60, c="giallo", etichetta="Cluster5") plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="Nero", etichetta="centroidi") plt.xlabel('Reddito annuo (k$)') plt.ylabel('Punteggio di spesa (1-100)') plt.legend() plt.mostra()
Grafico:
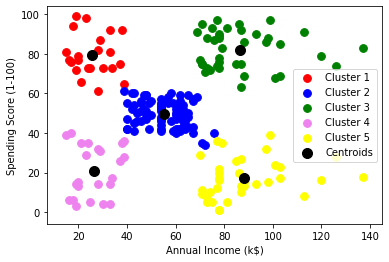
Come puoi vedere c'è 5 gruppi in totale che vengono visualizzati in colori diversi e il baricentro di ciascun gruppo è visualizzato in nero.
Codice completo
# Importazione delle librerie importa numpy come np importa matplotlib.pyplot come plt importa panda come pd # Importazione del set di dati X = dataset.iloc[:, [3, 4]].valori set di dati = pd.read_csv('Clienti_centro commerciale.csv') da sklearn.cluster importa KMeans # Utilizzando il metodo del gomito per trovare il numero ottimale di cluster wcss = [] per io nel raggio d'azione(1, 11): wcss.append(kmeans.inerzia_) kmsignifica = KMezzi(n_cluster = i, inizia="k-significa++", stato_casuale = 42) kmeans.fit(X) plt.trama(gamma(1, 11), wcss) plt.xlabel('Numero di cluster') y_kmeans = kmeans.fit_predict(X) plt.ylabel('WCSS') plt.mostra() # Addestramento del modello K-Means sul dataset kmeans = KMeans(n_cluster = 5, inizia="k-significa++", stato_casuale = 42) y_kmeans = kmeans.fit_predict(X) # Visualizzazione dei cluster plt.scatter( X[y_ksignifica == 1, 0], X[y_ksignifica == 1, 1], s = 60, c="blu", etichetta="Cluster2") plt.scatter( X[y_ksignifica == 0, 0], X[y_ksignifica == 0, 1], s = 60, c="rosso", etichetta="Cluster1") plt.scatter( X[y_ksignifica == 2, 0], X[y_ksignifica == 2, 1], s = 60, c="verde", etichetta="Cluster3") plt.scatter( kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="Nero", etichetta="centroidi") plt.scatter( X[y_ksignifica == 3, 0], X[y_ksignifica == 3, 1], s = 60, c="Viola", etichetta="Cluster4") plt.scatter( X[y_ksignifica == 4, 0], X[y_ksignifica == 4, 1], s = 60, c="giallo", etichetta="Cluster5") plt.xlabel('Reddito annuo (k$)') plt.ylabel('Punteggio di spesa (1-100)') plt.legend() plt.mostra()
conclusione
Questo è il concetto di base dell'algoritmo di clustering K-means nell'apprendimento automatico. Nei prossimi articoli, possiamo saperne di più sui diversi algoritmi di apprendimento automatico.
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.
