Nota: Questo articolo è stato originariamente pubblicato su 10 ottobre 2014 e il 27 marzo 2018.
Panoramica
- Capire il vicino più prossimo (KNN): uno degli algoritmi di apprendimento automatico più popolari
- Scopri come funziona kNN in Python
- Scegli il valore corretto di K in parole povere
introduzione
Nei quattro anni della mia carriera nella scienza dei dati, Ho costruito più di 80% di modelli di classificazione e solo uno 15-20% modelli di regressione. Queste proporzioni possono essere più o meno generalizzate in tutto il settore. La ragione di questo pregiudizio verso modelli di classificazione è che la maggior parte dei problemi analitici implica prendere una decisione.
Ad esempio, se un cliente si esaurirà o meno, se andiamo al cliente X per le campagne digitali, se il cliente ha un alto potenziale o no, eccetera. Queste analisi sono più approfondite e sono direttamente collegate a una roadmap di implementazione.
In questo articolo, parleremo di un altro machine learning ampiamente utilizzato. tecnica di classificazioneme chiamati K-vicini più vicini (KNN). Il nostro focus sarà principalmente su come funziona l'algoritmo e su come il parametro di input influenza l'output / predizione.
Nota: Le persone che preferiscono imparare attraverso i video possono imparare lo stesso attraverso il nostro corso gratuito – Algoritmo K-vicini più vicini (KNN) in Python e R. E se sei un principiante assoluto nella scienza dei dati e nell'apprendimento automatico, dai un'occhiata al nostro programma Certified BlackBelt:
Sommario
- Quando usiamo l'algoritmo KNN??
- Come funziona l'algoritmo KNN??
- Come scegliamo il fattore K??
- Abbattendolo – Pseudo codice KNN
- Implementazione di Python da zero
- Confrontando il nostro modello con scikit-learn
Quando usiamo l'algoritmo KNN??
KNN può essere utilizzato per la classificazione predittiva e problemi di regressione. tuttavia, più ampiamente utilizzato nei problemi di classificazione nell'industria. Per valutare qualsiasi tecnica, di solito guardiamo 3 aspetti importanti:
1. Facilità di interpretazione dell'output
2. Tempo di calcolo
3. Potere predittivo
Facciamo alcuni esempi per posizionare KNN sulla bilancia:
Ferias de algoritmos KNN a través de todos los parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... de consideraciones. È comunemente usato per la sua facile interpretazione e il basso tempo di calcolo.
Come funziona l'algoritmo KNN??
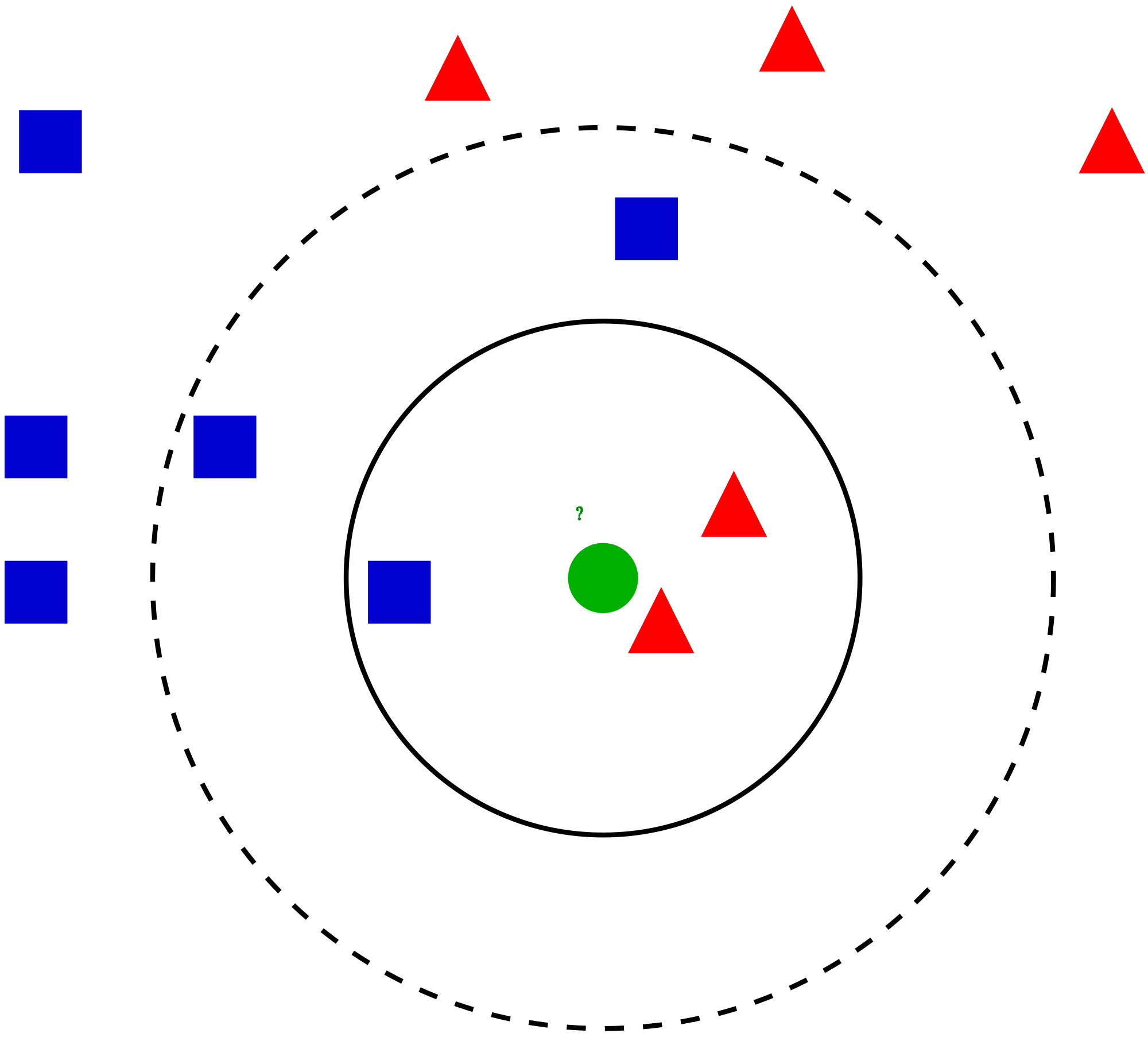
Prendiamo un caso semplice per capire questo algoritmo. Di seguito è riportata un'estensione dei cerchi rossi (RC) e quadrati verdi (GS):
Ha intenzione di scoprire la classe della stella blu (BS). BS può essere RC o GS e nient'altro. L'algoritmo “K” it KNN è il vicino più prossimo per cui vogliamo votare. Diciamo che K = 3. Perciò, ora faremo un cerchio con BS come centro così grande da racchiudere solo tre punti dati nel piano. Si prega di fare riferimento allo schema seguente per maggiori dettagli:
I tre punti più vicini a BS sono tutti RC. Perciò, con un buon livello di fiducia, possiamo dire che il BS dovrebbe appartenere alla classe RC. Qui, la scelta è diventata molto ovvia in quanto i tre voti del vicino più prossimo sono andati a RC. La scelta del parametro K è molto importante in questo algoritmo. Prossimo, capiremo quali sono i fattori da considerare per concludere al meglio K.
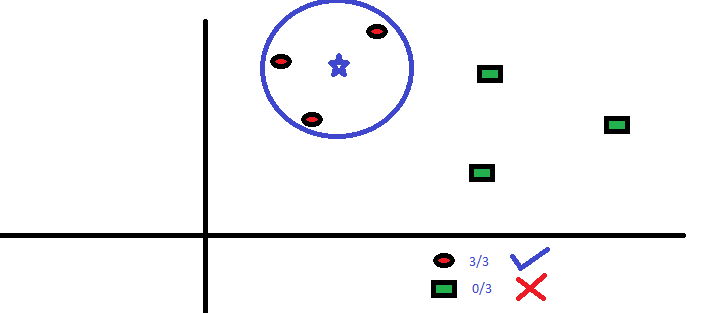
Come scegliamo il fattore K??
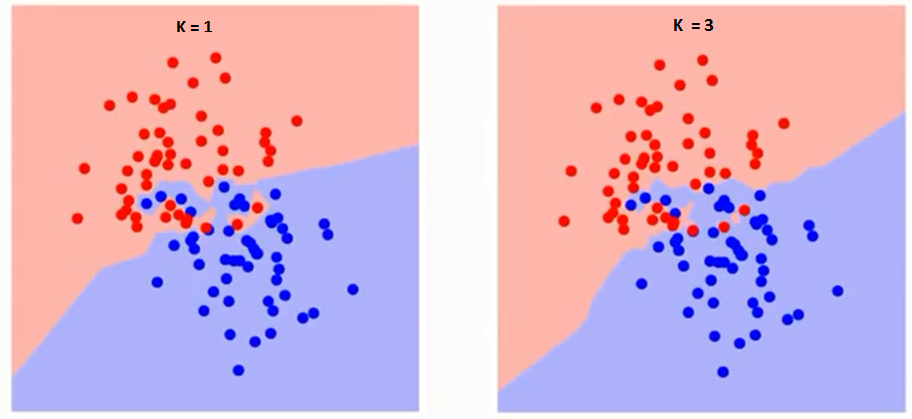
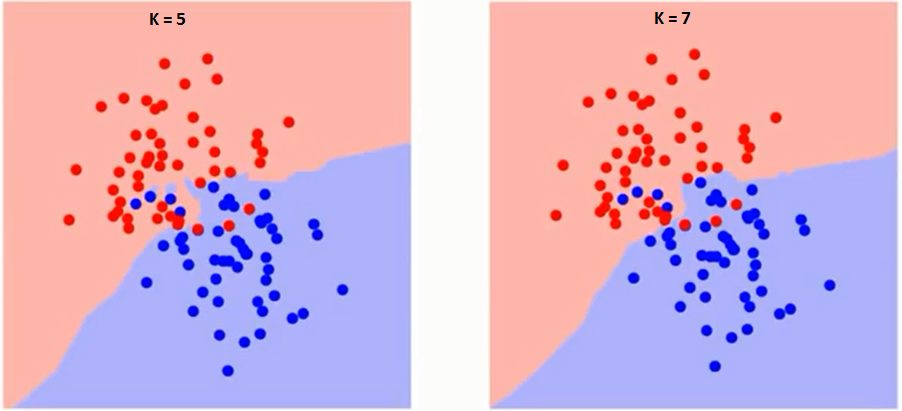
Cerchiamo prima di capire cosa esattamente K influenza l'algoritmo. Se vediamo l'ultimo esempio, dal momento che 6 observaciones de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.... permanecen constantes, con un dato valore di K possiamo porre dei limiti per ogni classe. Questi limiti separeranno RC da GS. Nello stesso modo, proviamo a vedere l'effetto del valore “K” nei limiti della classe. Di seguito i diversi limiti che separano le due classi con differenti valori di K.
Se guardi da vicino, puoi vedere che il limite diventa più liscio all'aumentare del valore di K. Con K crescente all'infinito, alla fine diventa tutto blu o tutto rosso, a seconda della maggioranza totale. Il tasso di errore di addestramento e il tasso di errore di convalida sono due parametri di cui abbiamo bisogno per accedere a diversi valori K.. A continuación se muestra la curva para la tasa de error de entrenamiento con un valor variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... de K:
Come potete vedere, il tasso di errore in K = 1 è sempre zero per il campione di allenamento. Questo perché il punto più vicino a qualsiasi punto dati di addestramento è se stesso, quindi la previsione è sempre accurata con K = 1. Se la curva dell'errore di convalida fosse stata simile, la nostra scelta di K sarebbe stata 1. Di seguito è riportata la curva dell'errore di validazione con un valore variabile di K:
Questo cancella la storia. E K = 1, stavamo oltrepassando i limiti. Perciò, il tasso di errore inizialmente diminuisce e raggiunge il minimo. Dopo il punto di minimo, aumenta con l'aumentare di K. Per ottenere il valore ottimale di K, può separare la formazione e la convalida iniziale del set di dati. Ora traccia la curva dell'errore di convalida per ottenere il valore ottimale di K. Questo valore di K dovrebbe essere utilizzato per tutte le previsioni.
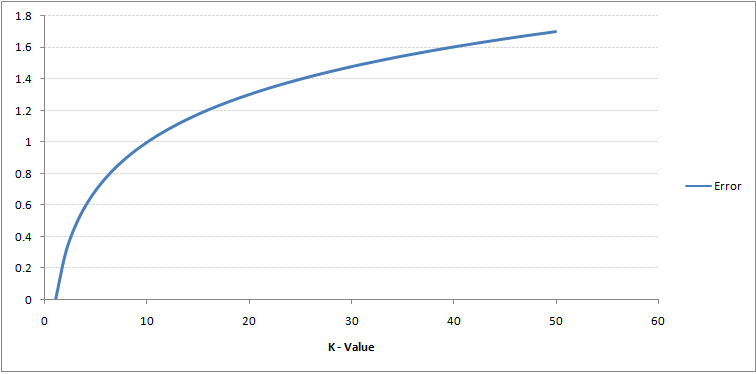
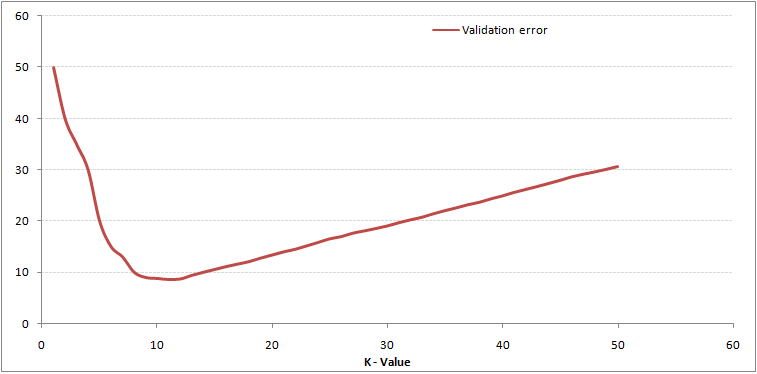
Il contenuto di cui sopra può essere compreso in modo più intuitivo utilizzando il nostro corso gratuito: Algoritmo dei vicini più vicini (KNN) in Python e R
Abbattendolo – Pseudo codice KNN
Possiamo implementare un modello KNN seguendo i passaggi seguenti:
- Caricare dati
- Inizializza il valore di k
- Per ottenere la classe prevista, ripetere da 1 fino al numero totale di punti dati di formazione
- Calcolare la distanza tra i dati del test e ogni riga di dati di allenamento. Qui useremo la distanza euclidea come metrica della distanza, in quanto è il metodo più popolare. Le altre metriche che possono essere utilizzate sono Chebyshev, coseno, eccetera.
- Ordinare le distanze calcolate in ordine crescente in base ai valori di distanza
- Ottenere le prime k righe dell'array ordinato
- Ottieni la classe più frequente in queste righe
- Restituisce la classe prevista
Implementazione di Python da zero
Useremo il popolare set di dati Iris per costruire il nostro modello KNN. Puoi scaricarlo da qui.
Confrontando il nostro modello con scikit-learn
from sklearn.neighbors import KNeighborsClassifier neigh = KNeighborsClassifier(n_neighbors=3) neigh.fit(data.iloc[:,0:4], dati['Nome']) # Predicted class print(neigh.predict(test)) -> ['Iris-virginica'] # 3 nearest neighbors print(neigh.kneighbors(test)[1]) -> [[141 139 120]]
Possiamo vedere che entrambi i modelli hanno previsto la stessa classe ('Iris-virginica') e gli stessi vicini più vicini ( [141 139 120] ). Perciò, possiamo concludere che il nostro modello funziona come previsto.
Implementazione di kNN in R
passo 1: importare i dati
passo 2: Verificare i dati e calcolare il riepilogo dei dati
Produzione
#Top observations present in the data SepalLength SepalWidth PetalLength PetalWidth Name 1 5.1 3.5 1.4 0.2 Iris-setosa 2 4.9 3.0 1.4 0.2 Iris-setosa 3 4.7 3.2 1.3 0.2 Iris-setosa 4 4.6 3.1 1.5 0.2 Iris-setosa 5 5.0 3.6 1.4 0.2 Iris-setosa 6 5.4 3.9 1.7 0.4 Iris-setosa #Check the dimensions of the data [1] 150 5 #Summarise the data SepalLength SepalWidth PetalLength PetalWidth Name Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 Iris-setosa :50 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 Iris-versicolor:50 Mediare :5.800 Mediare :3.000 Mediare :4.350 Mediare :1.300 Iris-verginica :50 Significare :5.843 Significare :3.054 Significare :3.759 Significare :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
passo 3: suddivisione dei dati
passo 4: Calcola la distanza euclidea
passo 5: Scrivere la funzione per prevedere KNN
passo 6: Calcolo dell'etichetta (Nome) per K = 1
Produzione
Per K=1 [1] "Iris-verginica"
Nello stesso modo, può calcolare altri valori di K.
Confronto della nostra funzione di previsione kNN con la libreria “Classe”
Produzione
Per K=1 [1] "Iris-verginica"
Possiamo vedere che entrambi i modelli hanno previsto la stessa classe ('Iris-virginica').
Note finali
L'algoritmo KNN è uno degli algoritmi di classificazione più semplici. Anche con tanta semplicità, può dare risultati altamente competitivi. L'algoritmo KNN può essere utilizzato anche per problemi di regressione. L'unica differenza con la metodologia discussa sarà l'uso delle medie dei vicini più prossimi invece di votare per i vicini più prossimi.. KNN può essere codificato su una singola riga in R. Devo ancora esplorare come possiamo usare l'algoritmo KNN in SAS.
L'articolo ti è stato utile?? Hai usato altri strumenti di machine learning di recente?? Hai intenzione di utilizzare KNN in uno qualsiasi dei tuoi problemi aziendali?? Se è così, dicci come pensi di farlo.
