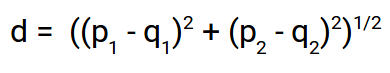Somiglianza immagine | Implementa la somiglianza delle immagini in Python

Se pensi che la nostra immagine di prova sia simile alla nostra prima immagine di riferimento, È giusto. Se credi il contrario, Scopriamolo insieme al potere della matematica e della programmazione.

“Il futuro della ricerca si concentrerà sulle immagini anziché sulle parole chiave”. – Ben Silbermann, CEO di Pinterest.

Immagine vettoriale

Ogni immagine è memorizzata nel nostro computer sotto forma di numeri e un vettore di tali numeri che può descrivere completamente la nostra immagine è noto come Image Vector.

distanza euclidea:

La distanza euclidea rappresenta la distanza tra due punti qualsiasi in uno spazio n-dimensionale. Dal momento che rappresentiamo le nostre immagini come vettori di immagini, non sono altro che un punto in uno spazio di n dimensioni e useremo la distanza euclidea per trovare la distanza tra loro.

Istogramma:

Un istogramma è una visualizzazione grafica di valori numerici. Useremo il vettore immagine per le tre immagini e poi troveremo la distanza euclidea tra loro. In base ai valori restituiti, l'immagine con una distanza minore è più simile dell'altra.

Per trovare la somiglianza tra le due immagini, useremo il seguente approccio:

1. Leggi i file immagine come un array.
2. Poiché i file di immagine sono colorati, ci sono 3 canali per i valori RGB. Li appiattiremo in modo che ogni immagine sia una singola matrice 1-D.
3. Una volta che abbiamo i nostri file immagine come un array, genereremo un istogramma per ogni immagine dove per ogni indice 0-255 contiamo l'occorrenza di quel valore di pixel nell'immagine.
4. Una volta che abbiamo i nostri istogrammi, useremo la regola L2 o la distanza euclidea per trovare la differenza tra i due istogrammi.
5. In base alla distanza tra l'istogramma della nostra immagine di prova e le immagini di riferimento, possiamo trovare l'immagine a cui la nostra immagine di prova è più simile..

Codifica per la somiglianza delle immagini in Python

Importare le dipendenze che useremo

from PIL import Image
from collections import Counter
import numpy as np

Useremo NumPy per salvare l'immagine come matrice NumPy, Immagine per leggere l'immagine in termini di valori numerici e Contatore per contare il numero di volte in cui si verifica ogni valore di pixel (0-255) nelle immagini.

Leggi l'immagine

reference_image_1 = Image.open('Immagine_di_riferimento1.jpg')
reference_image_arr = np.asarray(reference_image_1)
Stampa(np.forma(reference_image_arr))
>>> (250, 320, 3)

Possiamo vedere che la nostra immagine è stata letta correttamente come una matrice 3D. Nel prossimo passo, dobbiamo appiattire questa matrice 3D in una matrice unidimensionale.

flat_array_1 = array1.flatten()
Stampa(np.forma(flat_array_1))
>>> (245760, )

Faremo gli stessi passaggi per le altre due immagini. Lo salterò qui così puoi testarlo ulteriormente.

Generazione del vettore dell'istogramma di conteggio:

RH1 = Contatore(flat_array_1)

La riga di codice successiva restituisce un dizionario in cui la chiave corrisponde al valore del pixel e il valore della chiaveèil numero di volte in cui il pixelèpresente nell'immagine.

Una limitazione della distanza euclidea è che ha bisogno di tutti i vettori per essere normalizzati, In altre parole, entrambi i vettori devono avere le stesse dimensioni. Per assicurarci che il nostro vettore dell'istogramma sia normalizzato, useremo un ciclo per of 0-255 e genereremo il nostro istogramma con il valore della chiave se la chiave è presente nell'immagine; caso opposto, aggiungiamo a 0.

H1 = []
per io nel raggio d'azione(256):
    se sono in RH1.keys():
        H1.append(D1[io])
    altro:
        H1.append(0)

Il frammento di codice sopra genera un vettore di dimensioni (256,) donde cada indiceIl "Indice" È uno strumento fondamentale nei libri e nei documenti, che consente di individuare rapidamente le informazioni desiderate. In genere, Viene presentato all'inizio di un'opera e organizza i contenuti in modo gerarchico, compresi capitoli e sezioni. La sua corretta preparazione facilita la navigazione e migliora la comprensione del materiale, rendendolo una risorsa essenziale sia per gli studenti che per i professionisti in vari settori.... corresponde al valor del píxel y el valor corresponde al recuento del píxel en esa imagen.

Seguiamo gli stessi passaggi per le altre due immagini e otteniamo i loro corrispondenti Count-Histogram-Vectors. A questo punto, abbiamo i nostri vettori finali sia per le immagini di riferimento che per l'immagine di prova e tutto ciò che faremo è calcolare le distanze e prevedere.

Funzione di distanza euclidea:

def L2Norm(H1, H2):
    distance =0
    for i in range(len(H1)):
        distanza += np.quadrato(H1[io]-H2[io])
    ritorno np.sqrt(distanza)

La función anterior toma dos istogrammiGli istogrammi sono rappresentazioni grafiche che mostrano la distribuzione di un set di dati. Sono costruiti dividendo l'intervallo di valori in intervalli, oh "Bidoni", e il conteggio della quantità di dati che cadono in ogni intervallo. Questa visualizzazione consente di identificare i modelli, tendenze e variabilità dei dati in modo efficace, facilitare l'analisi statistica e il processo decisionale informato in varie discipline.... y devuelve la distancia euclidiana entre ellos.

Valutazione:

Dal momento che abbiamo tutto il necessario per trovare le somiglianze nell'immagine, Scopriamo la distanza tra l'immagine di prova e la nostra prima immagine di riferimento.

dist_test_ref_1 = L2Norm(H1, test_H)
Stampa("La distanza tra Reference_Image_1 e Test Image è : {}".formato(dist_test_ref_1))
>>> La distanza tra Reference_Image_1 e Test Image è : 9882.175468994668

Scopriamo ora la distanza tra l'immagine di prova e la nostra seconda immagine di riferimento.

dist_test_ref_2 = L2Norm(H2, test_H)
Stampa("La distanza tra Reference_Image_2 e Test Image è : {}".formato(dist_test_ref_2))
>>> La distanza tra Reference_Image_2 e Test Image è : 137929.0223122023

conclusione

Sulla base dei risultati precedenti, possiamo vedere che la distanza tra la nostra immagine di prova e la nostra prima immagine di riferimento è molto più piccola della distanza tra il nostro test e la nostra seconda immagine di riferimento, il che ha senso perché sia ​​l'immagine di prova che la nostra prima immagine di riferimento sono immagini Piegon mentre la nostra seconda immagine di riferimento è di un pavone.

Nel prossimo tutorial, abbiamo imparato come usare la matematica di base e poca programmazione per costruire il nostro predittore di somiglianza dell'immagine con risultati abbastanza decenti.

Il codice completo lo trovate insieme alle immagini. qui.

Circa l'autore

Mi chiamo Prateek Agrawal e sono uno studente del terzo anno presso l'Indian Institute of Design and Manufacturing of Information Technology Kancheepuram, perseguire la mia doppia laurea B.Tech e M.Tech in Informatica. Ho sempre avuto un talento per l'apprendimento automatico e la scienza dei dati e l'ho praticato nell'ultimo anno circa e ho alcune vittorie alle spalle..

Personalmente credo che La passione è tutto ciò di cui hai bisogno. Ricordo di essermi spaventato nel sentire la gente parlare della CNNS, RNN e Deep Learning perché non riuscivo a capire una singola parte, ma non mi sono arreso. Ho avuto la passione e ho iniziato a fare piccoli passi verso l'apprendimento ed eccomi qui a postare il mio primo blog. Spero che ti sia piaciuto leggere questo e ti senti un po' sicuro di te. Fidati di me su questo, sì posso, Puoi.

Per favore, scrivimi in caso di domande o solo per salutarmi.

LinkedIn: https://www.linkedin.com/in/prateekagrawal1405/
Github: https://github.com/prateekagrawaliiit

Titoli di coda

• Wikipedia
• AnalisiL'analisi si riferisce al processo di raccolta, Misura e analizza i dati per ottenere informazioni preziose che facilitano il processo decisionale. In vari campi, come business, Salute e sport, L'analisi può identificare modelli e tendenze, Ottimizza i processi e migliora i risultati. L'utilizzo di strumenti avanzati e tecniche statistiche è fondamentale per trasformare i dati in conoscenze applicabili e strategiche.... Vidhya
• Metà
• Google Immagini