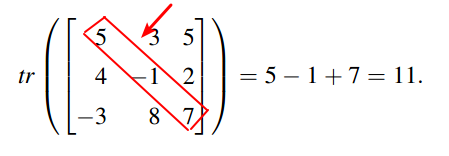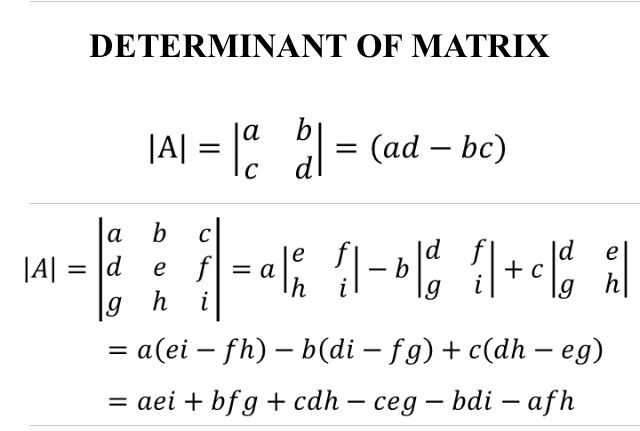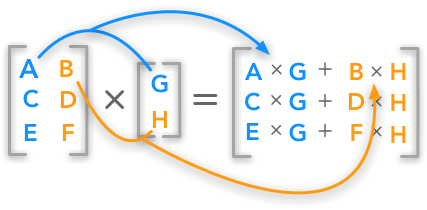Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati
introduzione
Si comienza a aprender el apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute..., La prima cosa a cui verrai esposto sono i concetti di algebra lineare che ti danno una migliore intuizione su come gli algoritmi funzionano effettivamente sotto il cofano., permettendoti di prendere decisioni migliori. En Deep Learning, un neuronale rossoLe reti neurali sono modelli computazionali ispirati al funzionamento del cervello umano. Usano strutture note come neuroni artificiali per elaborare e apprendere dai dati. Queste reti sono fondamentali nel campo dell'intelligenza artificiale, consentendo progressi significativi in attività come il riconoscimento delle immagini, Elaborazione del linguaggio naturale e previsione delle serie temporali, tra gli altri. La loro capacità di apprendere schemi complessi li rende strumenti potenti.. de avance es una red muy simple y muy útil. Underhood, la rete neurale che alimenta in avanti è solo una funzione composita, che moltiplica tra loro alcune matrici e vettori.
Fonte immagine: Collegamento
Non è che vettori e matrici siano l'unico modo per eseguire queste operazioni, ma diventano altamente efficienti se lo fai. Le strutture di dati centrali alla base del deep learning includono
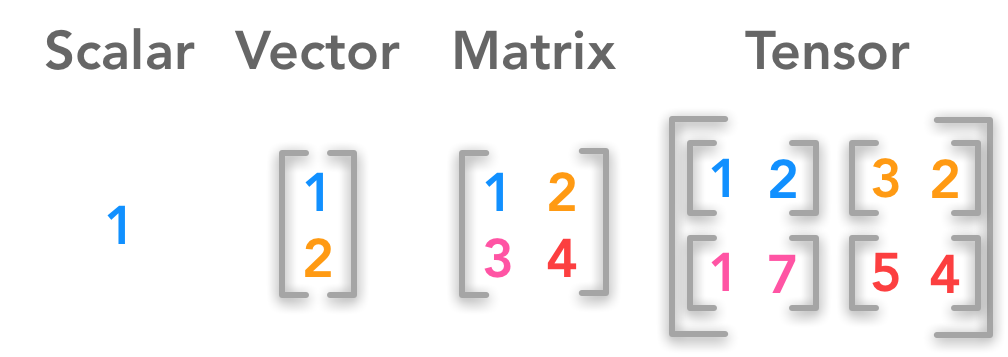
- scalari
- Vettore dei cartoni animati,
- Matrici e
- Tenditori.
Le operazioni di matrice sono utilizzate nella descrizione di molti algoritmi di deep learning.
Fonte immagine: Collegamento
Quindi, se vuoi davvero essere un professionista nel campo del Deep Learning, non puoi smettere di padroneggiare alcuni di questi concetti. Quindi, in questo articolo, Discuteremo importanti operazioni di matrice di algebra lineare che vengono utilizzate nella descrizione dei metodi di deep learning..
Sommario
Gli argomenti che tratteremo in questo articolo sono i seguenti:
- Cosa sono le matrici?
- Come aggiungere e sottrarre matrici diverse?
- Come trovare la forma e la dimensione di un dato array?
- Come convertire una matrice densa in una matrice sparsa?
- Come trovare la trasposta di una matrice?
- Come trovare il mezzo, la varianza e la deviazione standard di una matrice?
- Come trovare la traccia di una matrice?
- Come estrarre gli elementi minimo e massimo da un array?
- Come trovare il determinante di una matrice?
- Come moltiplicare le matrici date?
- Come applicare la particolare operazione a ciascun elemento di un array?
- Come trovare l'inversa di una matrice?
- Come rimodellare la matrice in una dimensione diversa?
Cosa sono le matrici?
Gli array sono array rettangolari composti da numeri e possono essere visualizzati come 2Nord Dakota-ordine dei tenditori. Se m e n sono numeri interi positivi, vale a dire, m, n ∈ ℕ allora la matrice m × n contiene m * n numero di elementi, con m numero di righe e n numero di colonne.
La rappresentazione pittorica di una matrice m × n è mostrata di seguito:
Fonte immagine: Collegamento
Qualche volta, invece di descrivere i componenti completi dell'array, usiamo la seguente abbreviazione di matrice:
Ad esempio-
In questo esempio, con l'aiuto di numpy library, creeremo un array. Y también verifique la dimensione"Dimensione" È un termine che viene utilizzato in varie discipline, come la fisica, Matematica e filosofia. Si riferisce alla misura in cui un oggetto o un fenomeno può essere analizzato o descritto. In fisica, ad esempio, Si parla di dimensioni spaziali e temporali, mentre in matematica può riferirsi al numero di coordinate necessarie per rappresentare uno spazio. Comprenderlo è fondamentale per lo studio e... de la matriz formada.
importa numpy come np
matrice = np.array([[45,34],[67,58]])
# Crea una matrice
Stampa("La matrice originale è data da n", matrice)
# Controlla la dimensione della matrice
Stampa("La dimensione della matrice data è", matrice.ndim)
Produzione:
La matrice originale è data da [[45 34] [67 58]] La dimensione della matrice data è 2
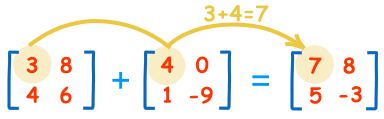
Addizione e sottrazione di matrici
Fonte immagine: Collegamento
In questa sezione, eseguiremo addizioni e sottrazioni di matrici usando il metodi addizione e sottrazione. Questi metodi accettano due argomenti e restituiscono rispettivamente la somma e la differenza di quelle matrici. Se la forma delle matrici non è la stessa, genera un errore che dice, l'addizione o la sottrazione non è possibile.
matrice_1 = np.array([[45,34],[67,58]])
matrice_2 = np.array([[35,24],[57,48]])
# Somma le due matrici
Stampa("Il risultato dopo aver aggiunto la matrice 1 e matrice 2 è dato da n" , np.add(matrice_1, matrice_2))
# Sottrarre una matrice dalle altre matrici
Stampa("Il risultato dopo aver sottratto matrice 1 da matrice 2 è dato da n" , np.sottrarre(matrice_1, matrice_2))
Stampa("Il risultato dopo aver sottratto matrice 2 da matrice 1 è dato da n" , np.sottrarre(matrice_2, matrice_1))
Produzione:
Il risultato dopo aver aggiunto la matrice 1 e matrice 2 è dato da [[ 80 58] [124 106]] Il risultato dopo aver sottratto matrice 1 da matrice 2 è dato da [[10 10] [10 10]] Il risultato dopo aver sottratto matrice 2 da matrice 1 è dato da [[-10 -10] [-10 -10]]
Forma e dimensione di un array
In questa sezione, troveremo la strada, vale a dire, il numero di righe e colonne nella matrice data e la dimensione, vale a dire, il numero di elementi nell'array di un dato array.
matrice = np.array([[45,34,75],[67,58,89]])
# Trovare il numero di righe e colonne nella matrice
Stampa("Il numero di righe e colonne nella matrice data è " + str(matrice.forma[0]) + " e " + str(matrice.forma[1]) + " rispettivamente")
# Numero di elementi nella matrice
Stampa("La dimensione della matrice data è" , matrice.dimensione)
Produzione:
Il numero di righe e colonne nella matrice data è 2 e 3 rispettivamente La dimensione della matrice data è 6
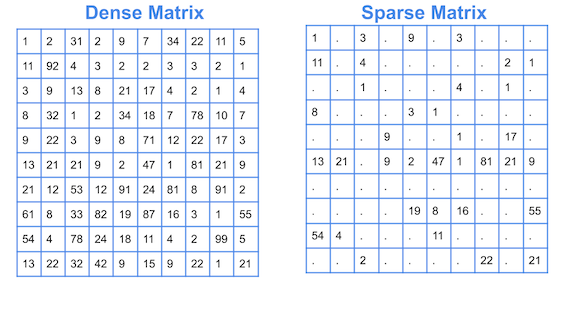
Conversione di una data matrice densa in una matrice sparsa
Capiamo prima cosa si intende esattamente per matrice sparsa e densa.
Una matrice sparsa è una matrice che consiste principalmente di valori zero. E le matrici sparse sono diverse dalle matrici con valori per lo più diversi da zero, che sono note come matrici dense.
Fonte immagine: Collegamento
da scipy import sparse
# Crea una matrice densa
matrice_densa = np.array([[0,0],[0,17],[78,0]])
# Converti matrice densa in matrice sparsa
sparse_matrix = sparse.csr_matrix(matrice_densa)
Stampa("La matrice sparsa corrispondente ad una data matrice densa è data da n" , matrice_sparsa)
Produzione:
La matrice sparsa corrispondente a una data matrice densa è data da (1, 1) 17 (2, 0) 78
Trasposizione della matrice
En Matrix Transpose, possiamo convertire un vettore riga in un vettore colonna e viceversa, vale a dire, la riga diventa colonne e le colonne diventano righe.
Se abbiamo la matrice A = [unij]mxn, quindi la trasposta di questa matrice è AT = [undal]n × m
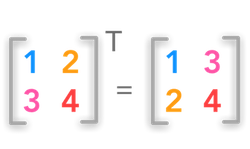
importa numpy come np
matrice = np.array([[45,34],[67,58]])
Stampa("La matrice originale è data da n" , matrice)
Stampa("La matrice trasposta della matrice data è n" , matrice.T)
Produzione:
La matrice originale è data da [[45 34] [67 58]] La matrice trasposta della matrice data è [[45 67] [34 58]]
Media, varianza e deviazione standard di una matrice
In questa sezione, proveremo a trovare alcune cose statistiche relative a un array. Qui calcoliamo la media, la varianza e la deviazione standard della matrice utilizzando le funzioni numpy.
importa numpy come np
matrice = np.array([[45,34],[67,58], [23,89]])
# Trovare la media degli elementi di una matrice
Stampa("La media degli elementi di una matrice è uguale a", np.significa(matrice))
# Trovare la varianza di elementi di una matrice
Stampa("La varianza degli elementi di una matrice è uguale a", np.var(matrice))
# Trovare la Deviazione Standard di elementi di una matrice
Stampa("La deviazione standard degli elementi di una matrice è uguale a", ad es. std(matrice))
Stampa("La deviazione standard degli elementi di una matrice è uguale a", np.sqrt(np.var(matrice)))
Produzione:
La media degli elementi di una matrice è uguale a 52.666666666666664 La varianza degli elementi di una matrice è uguale a 473.5555555555555 La deviazione standard degli elementi di una matrice è uguale a 21.761331658599286 La deviazione standard degli elementi di una matrice è uguale a 21.761331658599286
Traccia di una matrice
Fonte immagine: Collegamento
In questa sezione, proverò a trovare la traccia di una matrice, vale a dire, la somma di tutti gli elementi diagonali presenti in una data matrice.
importa numpy come np
matrice = np.array([[1,2,3],[4,5,6], [7,8,9]])
# Ottieni gli elementi diagonali di una matrice
Stampa("Gli elementi diagonali di una data matrice sono n", matrice.diagonale())
# Trovare la traccia della matrice
Stampa("La traccia di una data matrice è uguale a", matrice.diagonale().somma())
Produzione:
Gli elementi diagonali di una data matrice sono [1 5 9] La traccia di una data matrice è uguale a 15
Trova gli elementi minimi e massimi di una matrice
In questa sezione, proveremo a trovare gli elementi minimo e massimo di una matrice, vale a dire, l'articolo con il valore più alto e più basso tra tutti gli articoli.
importa numpy come np
matrice = np.array([[1,2,3],[4,5,6], [7,8,9]])
# Trova l'elemento minimo della matrice
Stampa("L'elemento minimo in una data matrice è", ad esempio min(matrice))
# Trova l'elemento massimo della matrice
Stampa("L'elemento massimo in una data matrice è", np.max(matrice))
Produzione:
L'elemento minimo in una data matrice è 1 L'elemento massimo in una data matrice è 9
Determinante di una matrice
Fonte immagine: Collegamento
In questa sezione, proveremo a trovare il determinante di una matrice. Qui, calcolare il determinante, usiamo il modulo di algebra lineare presente nel pacchetto Numpy.
importa numpy come np
matrice = np.array([[1,2,4],[3,4,6], [7,8,5]])
# Trova il determinante della matrice
Stampa("Il determinante della matrice data è uguale a", np.linalg.det(matrice))
Produzione:
Il determinante della matrice data è uguale a 9.999999999999993
Moltiplicazione di matrici
Una serie di forme (mxn) e una matrice B di forma (nxp) moltiplicato da C di forma (mxp). Ricorda che quando si moltiplicano le matrici è che il numero di colonne nella prima matrice è uguale al numero di righe nella seconda matrice per eseguire la moltiplicazione senza errori.
Fonte immagine: Collegamento
In questa sezione, proveremo a trovare la moltiplicazione di due matrici.
importa numpy come np
matrice_1 = np.array([[45,34],[67,58]])
matrice_2 = np.array([[35,24],[57,48]])
Stampa("La moltiplicazione matriciale di due matrici date è data da n", ad es. matmul(matrice_1, matrice_2))
Produzione:
La moltiplicazione matriciale di due matrici date è data da [[3513 2712] [5651 4392]]
Operazioni intelligenti con elementi che utilizzano una funzione in linea (Lambda)
In questo esempio, proveremo ad aggiungere un certo valore a ciascuno degli elementi di un array.
importa numpy come np
matrice = np.array([[1,2,4],[3,4,6], [7,8,5]])
addizione = lambda i:io+5
add_5_vec = np.vectorize(addizione)
Stampa("La matrice dopo aver aggiunto 5 a tutti i suoi elementi è n", add_5_vec(matrice))
Produzione:
La matrice dopo aver aggiunto 5 a tutti i suoi elementi è [[ 6 7 9] [ 8 9 11] [12 13 10]]
Inversa di una matrice
In questa sezione, proveremo a trovare l'inversa di una matrice.
importa numpy come np
matrice = np.array([[1,2,4],[3,4,6], [7,8,5]])
# Trovare l'inversa di una matrice
Stampa("La matrice inversa di una data matrice è n", np.linalg.inv(matrice))
Produzione:
La matrice inversa di una data matrice è [[-2.8 2.2 -0.4] [ 2.7 -2.3 0.6] [-0.4 0.6 -0.2]]
Rimodellare una determinata matrice
In questa sezione, proveremo a rimodellare una data matrice, vale a dire, cambia la forma della matrice data. Ma qui dobbiamo notare che la dimensione rimane costante dopo aver rimodellato la matrice, vale a dire, il numero di elementi rimane lo stesso.
importa numpy come np
matrice = np.array([[1,2,4],[3,4,6],[7,8,5],[9,2,1]])
Stampa("La matrice rimodellata è data da n", matrice.rimodellare(6,2))
Produzione:
La matrice rimodellata è data da [[1 2] [4 3] [4 6] [7 8] [5 9] [2 1]]
Altri miei post sul blog
Puoi anche dare un'occhiata ai miei precedenti post sul blog.
Post precedenti del blog sulla scienza dei dati.
Ecco qui il mio profilo Linkedin nel caso tu voglia connetterti con me. Sarò felice di essere connesso con te.
Per qualsiasi domanda, puoi scrivermi a Gmail.
Note finali
Grazie per aver letto!
Spero che l'articolo ti sia piaciuto. Se ti piace, condividilo anche con i tuoi amici. Tutto ciò che non è stato menzionato o vuoi condividere i tuoi pensieri? Sentiti libero di commentare qui sotto e ti ricontatterò. ?
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.