Ottimizzazione del portafoglio in Python | Teoria del portafoglio moderna in Python

introduzione

In questo articolo, Impareremo i concetti di gestione del portafoglio e li implementeremo utilizzando le librerie Python.

L'articolo è diviso in tre parti al fine di coprire i fondamenti della gestione del portafoglio come mostrato di seguito:

1. Rendimento su un asset e un portafoglio

2. Rischio associato a un asset e a un portafoglio

3. Teoria del portafoglio moderna: trova il portafoglio ottimale

Rendimento su un asset e un portafoglio

Prima di addentrarci nel calcolo dei rendimenti di un asset e di un portafoglio, visitiamo brevemente la definizione di portafoglio e rendimenti.

valigetta: Un portafoglio è una raccolta di strumenti finanziari come le azioni, obbligazioni, materiali grezzi, Liquidità e mezzi equivalenti, così come le loro controparti di fondi. [Investopedia]

In questo articolo, avremo il nostro portfolio che contiene 4 risorse (“Portafoglio incentrato sull'azionario“): Azioni di Apple Inc., Nike (NKC), Google e Amazon. L'anteprima dei nostri dati è mostrata di seguito:

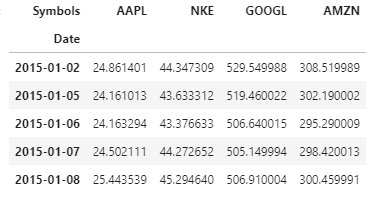
ritorna: Si riferisce al guadagno o alla perdita dei nostri beni / portafoglio a tempo determinato. In questa analisi, otteniamo un rendimento come variazione percentuale del prezzo di chiusura dell'attività rispetto al prezzo di chiusura del giorno precedente. Calcoleremo i rendimenti utilizzando.pct_change () funzione in Python.

Di seguito è riportato il codice Python per fare lo stesso e il 5 righe in alto (intestazione) di ritorni

Nota: la prima riga è Null se non esiste una riga precedente per facilitare il calcolo della variazione percentuale.

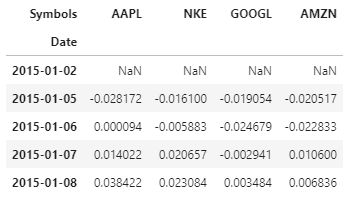
Restituire un portafoglio è definita come la somma ponderata dei rendimenti sulle attività in portafoglio.

Per dimostrare come calcolare le prestazioni del portafoglio in Python, inizializziamo i pesi in modo casuale (che poi ottimizzeremo). Il rendimento del portafoglio viene calcolato come mostrato nel codice seguente e viene visualizzata anche l'intestazione dei rendimenti del portafoglio:

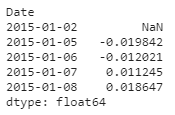
Abbiamo visto come calcolare i rendimenti, ora spostiamo la nostra attenzione su un altro concetto: Rischio

Il rischio associato alle attività e al portafoglio

Il metodo per calcolare il rischio di un portafoglio è scritto di seguito e successivamente spieghiamo e diamo la formulazione matematica per ciascuno dei passaggi:

• Calcola la matrice di covarianza sui dati delle prestazioni.
• Annualizzare la covarianza moltiplicando per 252
• Calcola la varianza del portafoglio moltiplicandolo per i vettori di peso.
• Calcola la radice quadrata della varianza calcolata sopra per ottenere la deviazione standard. Questa deviazione standard è chiamata volatilità del portafoglio.

La formula per calcolare la covarianza e annualizzarla è:

covarianza = restituisce.cov () * 252

Com'è lì 252 giorni lavorativi, moltiplichiamo la covarianza per 252 annualizzarlo.

La variazione del portafoglio, da calcolare in step 3 anteriore, dipende dai pesi delle attività in portafoglio ed è definita come:

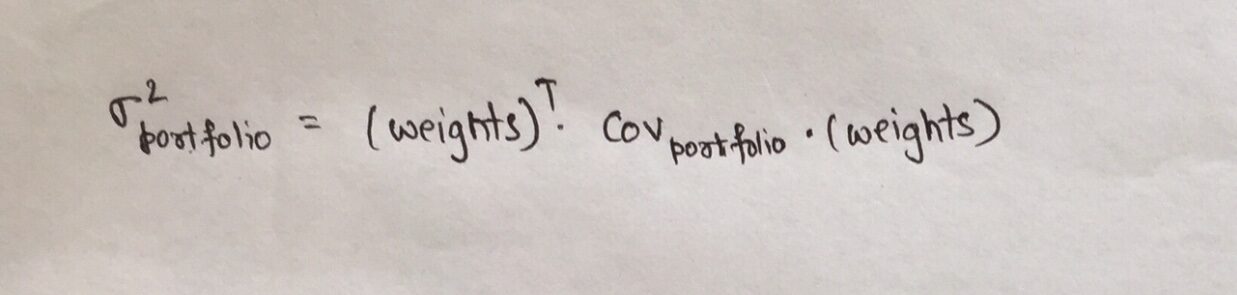
dove,

• Il_valigetta è la matrice di covarianza del portafoglio
• pesi è il vettore dei pesi assegnati a ciascun asset nel portafoglio

Di seguito è riportato l'approccio per calcolare il rischio patrimoniale in Python.

Come spiegato sopra, moltiplichiamo la matrice di covarianza con 252, visto che ci sono 252 giorni di negoziazione in un anno.

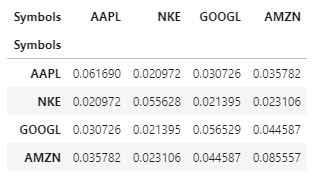
Gli elementi diagonali di varnce_matrix rappresentano la varianza di ciascun asset, mentre i termini fuori diagonale rappresentano la covarianza tra i due asset, ad esempio: l'elemento (1,2) rappresenta la covarianza tra Nike e Apple.

Il codice per calcolare il rischio di portafoglio in Python, il cui metodo abbiamo visto prima, è come mostrato:

Ora, il compito per noi è ottimizzare i pesi. Come mai? In modo che possiamo massimizzare il nostro rendimento o ridurre al minimo il nostro rischio, E lo facciamo usando la moderna teoria del portafoglio!!

Teoria del portafoglio moderna

La moderna teoria del portafoglio sostiene che le caratteristiche di rischio e rendimento di un investimento non dovrebbero essere considerate da sole, Piuttosto, dovrebbero essere valutati in base a come l'investimento influisce sul rischio complessivo e sul rendimento del portafoglio.. MPT mostra che un investitore può costruire un portafoglio di più attività che massimizzeranno i rendimenti per un dato livello di rischio.. Inoltre, dato un livello desiderato di rendimento atteso, un investitore può costruire un portafoglio con il minor rischio possibile. Basato su misure statistiche come varianza e correlazione, la performance di un singolo investitore è meno importante di come influisce sull'intero portafoglio. [Investopedia]

Questa teoria è riassunta nel seguente figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline..... Troviamo la frontiera come mostrato di seguito e massimizziamo il rendimento atteso per il livello di rischio o riduciamo al minimo il rischio per un dato livello di rendimento atteso.

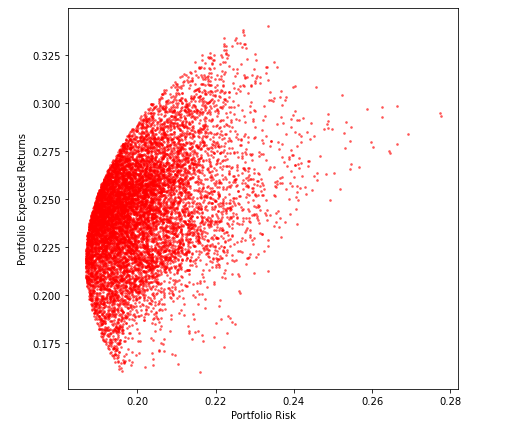
Il nostro obiettivo è scegliere i pesi per ogni asset nel nostro portafoglio in modo da massimizzare il rendimento atteso dato un livello di rischio..

Matematicamente, la funzione obiettivo può essere definita come mostrato di seguito:

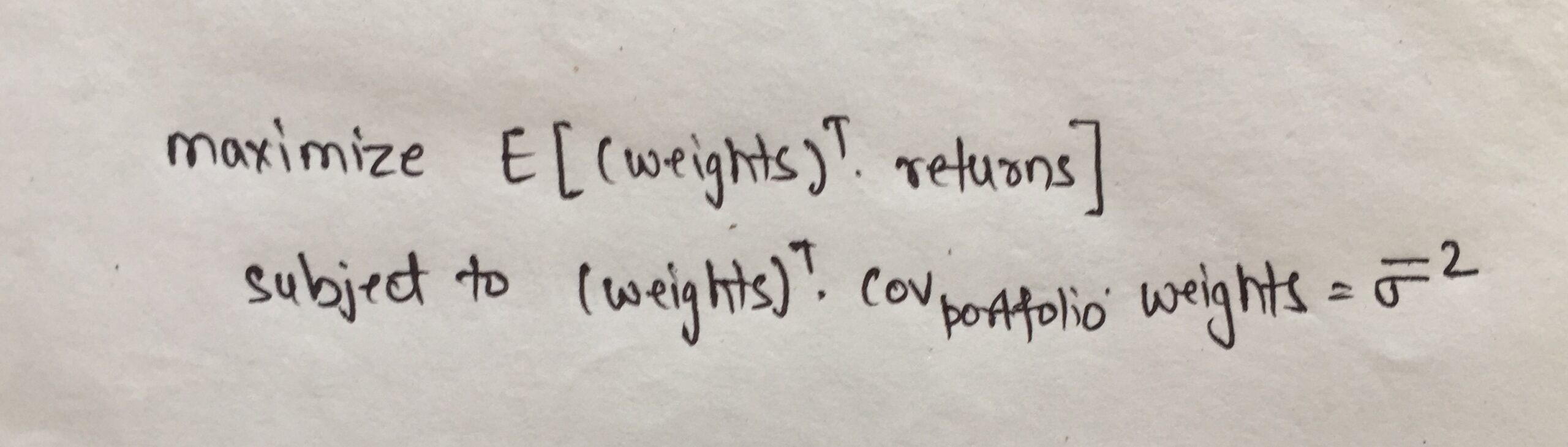
Un altro modo di guardare alla frontiera efficiente e alla funzione obiettivo è che possiamo minimizzare il rischio dato che il rendimento atteso è almeno maggiore del valore dato.. Matematicamente, questa funzione obiettivo può essere scritta come:

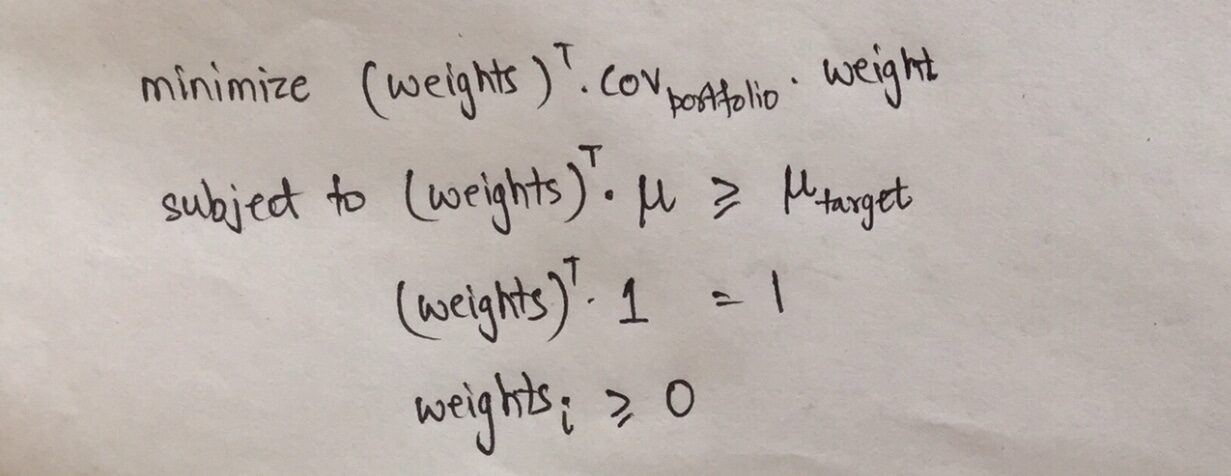
la prima riga rappresenta che l'obiettivo è minimizzare la varianza del portafoglio, vale a dire, a sua volta la volatilità del portafoglio e, perciò, minimizzare il rischio.

Restricted implica che i rendimenti devono essere maggiori di un particolare rendimento target, tutti i pesi devono essere aggiunti 1 e i pesi non devono essere negativi.

Ora che conosciamo il concetto, Passiamo ora alla parte pratica!

Primo, creiamo il confine efficiente eseguendo un ciclo. In ogni ciclo, consideriamo un diverso insieme di pesi assegnati casualmente per le attività nel nostro portafoglio e calcoliamo il rendimento e la volatilità per quella combinazione di pesi.

Per questo creiamo 3 liste vuote, uno per conservare i resi, un altro per memorizzare la volatilità e l'ultimo per memorizzare i pesi del portafoglio.

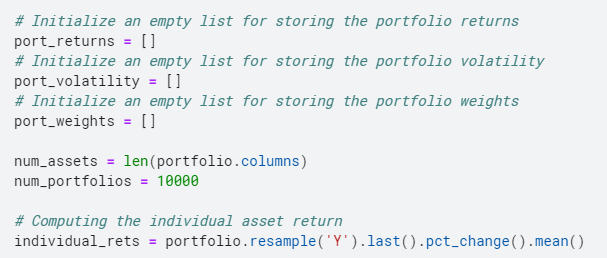
Una volta create le liste, generiamo casualmente i pesi delle nostre risorse ripetutamente, quindi normalizziamo la ponderazione per aggiungere 1. Quindi calcoliamo i rendimenti nello stesso modo in cui abbiamo calcolato sopra. Successivamente, Calcoliamo la varianza del portafoglio e poi prendiamo la radice quadrata e poi la annualizziamo per ottenere la volatilità, il misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... Rischio per il nostro portafoglio.

Ora aggreghiamo i dati in un dizionario e quindi creiamo un frame di dati per vedere la combinazione di pesi degli asset e i corrispondenti rendimenti e volatilità che generano.

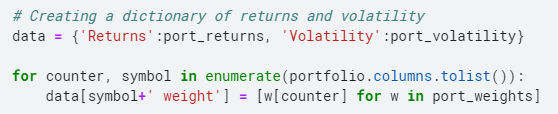
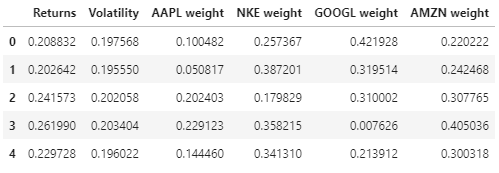
Ecco l'anteprima dei dati di redditività, volatilità e pesi del portafoglio.

Ora abbiamo tutto con noi per entrare nell'ultimo giro di questa gara e trovare il set di pesi ottimale!!

Tracciamo la volatilità rispetto ai rendimenti calcolati in precedenza, questo ci darà la frontiera efficiente che volevamo creare all'inizio di questo articolo.

Ed eccoci!!

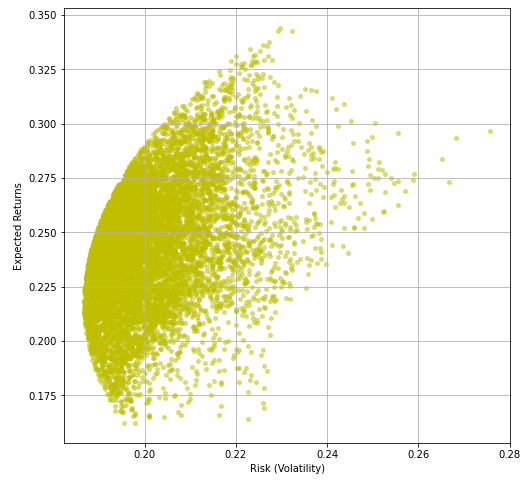
Ora che abbiamo con noi la frontiera efficiente, troviamo i pesi ottimali.

Possiamo ottimizzare l'uso di vari metodi come descritto di seguito:

• Portafoglio con volatilità minima (rischio)
• Portafoglio ottimale (Rapporto massimo di nitidezza)
• Rendimento massimo a livello di rischio; Rischio minimo a un livello di rendimento atteso; Portafoglio con il più alto rapporto Sortino

In questo articolo ottimizzerò attraverso i primi due approcci. Nel terzo segmento, il "Rendimento massimo a livello di rischio"’ e il "Rischio minimo a un livello di rendimento atteso"’ sono abbastanza semplici, mentre quello basato sul indiceIl "Indice" È uno strumento fondamentale nei libri e nei documenti, che consente di individuare rapidamente le informazioni desiderate. In genere, Viene presentato all'inizio di un'opera e organizza i contenuti in modo gerarchico, compresi capitoli e sezioni. La sua corretta preparazione facilita la navigazione e migliora la comprensione del materiale, rendendolo una risorsa essenziale sia per gli studenti che per i professionisti in vari settori.... è simile all'indice di Sharpe.

1. Volatilità minima

Per trovare la combinazione di volatilità minima, selezioniamo la riga nel nostro frame di dati che corrisponde alla varianza minima e troviamo quella riga usando la funzione .idxmin (). Il codice per fare lo stesso è mostrato di seguito:

I pesi che otteniamo da questo sono:

Ora, scopri dove si trova il punto più basso di volatilità sulla curva sopra. La risposta viene visualizzata alla fine! Ma non imbrogliare!

2. Rapporto di nitidezza più elevato

L'indice di Sharpe è il rendimento medio ottenuto in eccesso rispetto al tasso privo di rischio per unità di volatilità o rischio totale.. La formula utilizzata per calcolare l'indice di Sharpe è riportata di seguito:

Rapporto di nitidezza = (R_pagina – R_F)/ DAKOTA DEL ON_pagina

dove,

• R_pagina è il rendimento del portafoglio
• R_F è il tasso privo di rischio
• Dakota del sur_pagina è la deviazione standard dei rendimenti del portafoglio

Il codice per calcolare il portafoglio ottimale, vale a dire, portafoglio con il più alto indice di Sharpe, mostrato sotto:

Prossimo, Sono mostrati i pesi del portafoglio che danno l'indice di Sharpe più alto:

Scopri dove si trova il punto di relazione di Sharpe più alto sulla curva in alto. La risposta è mostrata di seguito! Un'altra volta, non imbrogliare!

Come promesso ecco la risposta alle due domande di cui sopra!!

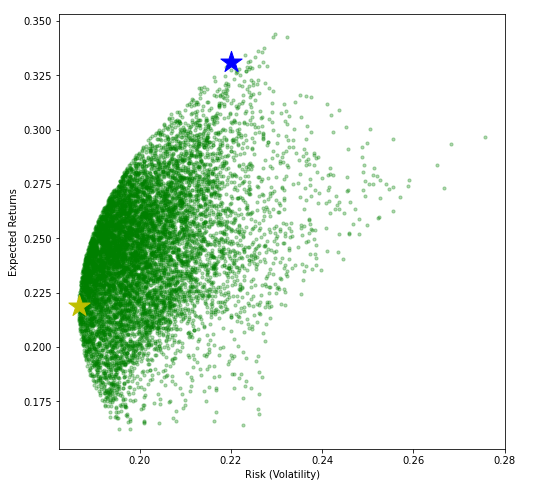
La stella blu corrisponde al punto di relazione Sharpe più alto e la stella gialla corrisponde al punto di minima volatilità.

Ora, prima di finire questo articolo, Ti incoraggio a trovare il portafoglio di rendimento massimo a un livello di rischio "e"’ Rischio minimo a un livello di redditività attesa 'e contrassegnarli nel grafico precedente.

Oltre a usare la relazione di Sharpe, possiamo anche ottimizzare il portafoglio utilizzando la relazione di Sortino.

Dare un breve su di esso:

il relazione Sortino è una variazione dell'indice di Sharpe che differenzia la volatilità dannosa dalla volatilità complessiva utilizzando la deviazione standard degli asset dei rendimenti negativi del portafoglio (deviazione verso il basso) invece della deviazione standard totale dei rendimenti del portafoglio. Il rapporto Sortino prende il rendimento di un'attività o portafoglio e sottrae il tasso privo di rischio, e quindi dividere tale importo per la deriva verso il basso dell'attività. [Investopedia]

Rapporto di ordinamento = (R_pagina – R_F)/ DAKOTA DEL OND

dove,

• R_pagina è il rendimento del portafoglio
• R_F è il tasso privo di rischio
• Dakota del surD è la deviazione standard dell'handicap

In caso di problemi nell'implementazione o nella comprensione del 3 metodi di ottimizzazione che ho descritto sopra, scrivimi a [e-mail protetta] | [e-mail protetta] | oppure contatta LinkedIn su https://www.linkedin.com/in/parth-tyagi-4b867452/

Nota sull'autore: Parth Tyagi sta attualmente studiando PGDBA all'IIM Calcutta, IIT Kharagpur & Indian Statistical Institute-Kolkata e ha completato il B.Tech da IIT Delhi. Ha ~ 4 anni di esperienza lavorativa nell'analisi avanzata.

Imparentato