Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Questo articolo ti darà chiarezza su cos'è la riduzione della dimensionalità, la tua esigenza e come funziona. C'è anche il codice Python per l'illustrazione e il confronto tra PCA, ICA e t-SNE.
Che cos'è la riduzione della dimensionalità e perché abbiamo bisogno di i
La riduzione della dimensionalità significa semplicemente ridurre il numero di funzioni (colonne) mantenendo la massima informazione. Di seguito sono riportati i motivi per la riduzione della dimensionalità:
- La riduzione della dimensionalità aiuta nella compressione dei dati e, così, riduce lo spazio di archiviazione.
- Riduci i tempi di calcolo.
- Aiuta anche a eliminare le funzioni ridondanti, si ci sono.
- Rimuovere le funzioni mappate.
- Ridurre le dimensioni dei dati a 2D o 3D può permetterci di tracciarli e visualizzarli con precisione. Prossimo, può vedere i modelli più chiaramente.
- È anche utile per rimuovere il rumore e, in conseguenza di ciò, possiamo migliorare
Esistono molti metodi per la riduzione della dimensionalità come PCA, ICA, t-SNE, eccetera., vedremo PCA (Analisi del componente principale).
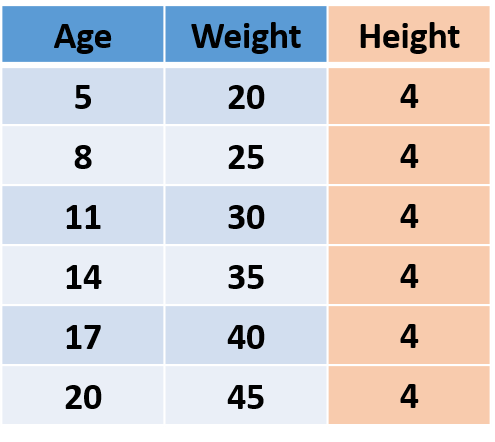
Prima capiamo di cosa si tratta informazione nei dati. Considera i seguenti dati immaginari, chi sono vecchi, il peso e l'altezza delle persone.
Figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... 1
Come "Altezza"’ di tutte le persone è lo stesso, vale a dire, la varianza è 0, quindi non aggiunge alcuna informazione, quindi possiamo eliminare la colonna "Altezza"’ senza perdere nessuna informazione.
Ora che sappiamo che l'informazione è varianza, Capiamo come funziona la PCA. In PCA, troviamo nuove dimensioni (caratteristiche) che catturano la varianza massima (vale a dire, informazione). Per capirlo useremo l'esempio precedente. Dopo aver rimosso "Altezza", Abbiamo "Età"’ e "Peso". Queste due caratteristiche si prendono cura di tutte le informazioni. In altre parole, possiamo dire che abbiamo bisogno 2 caratteristiche (Età e altezza) contenere le informazioni, e se riusciamo a trovare una nuova funzionalità che da sola può contenere tutte le informazioni, possiamo sostituire le caratteristiche di origine 2 con una nuova caratteristica unica, raggiungimento della riduzione della dimensionalità!
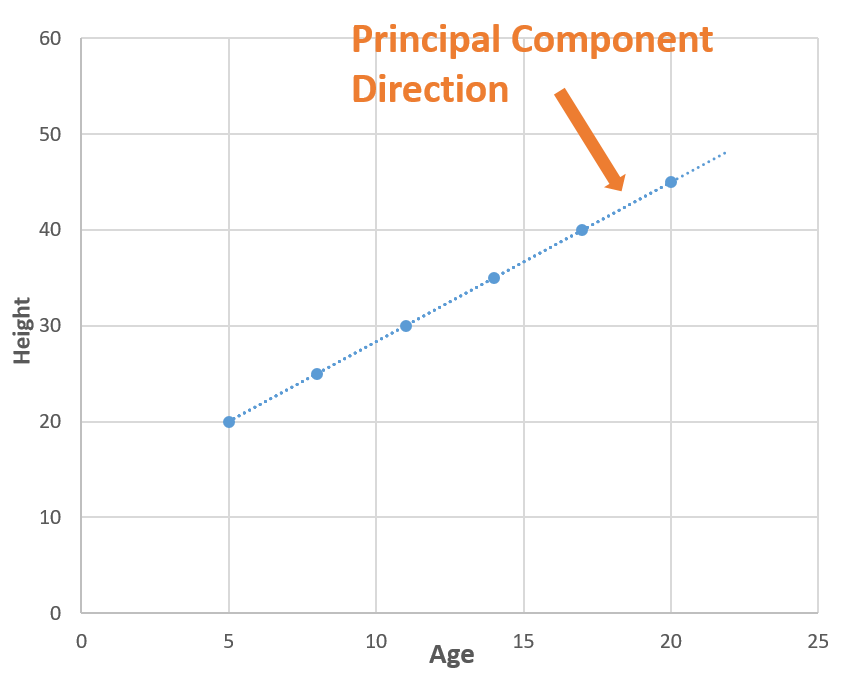
Ora considera una linea (linea tratteggiata blu) cosa passa attraverso tutti i punti?. La linea tratteggiata blu cattura tutte le informazioni, così possiamo sostituire "Età"’ e "Peso"’ (2 dimensioni) con linea tratteggiata blu (1 dimensione"Dimensione" È un termine che viene utilizzato in varie discipline, come la fisica, Matematica e filosofia. Si riferisce alla misura in cui un oggetto o un fenomeno può essere analizzato o descritto. In fisica, ad esempio, Si parla di dimensioni spaziali e temporali, mentre in matematica può riferirsi al numero di coordinate necessarie per rappresentare uno spazio. Comprenderlo è fondamentale per lo studio e...) senza perdere nessuna informazione, e in questo w
Ti chiedi come abbiamo trovato la linea tratteggiata blu (componente principale), quindi c'è molta matematica dietro.. Puoi leggere Questo articolo cosa spiega questo?, ma in parole semplici, troviamo le direzioni in cui possiamo cattura la massima varianza usando autovalori e autovettori.
Illustrazione della PCA in Python
Vediamo come usare PCA con un esempio. Ho usato dati sulla qualità del vino che hanno 12 caratteristiche come l'acidità, residuo zuccherino, cloruri, eccetera., e la qualità del vino per 1600 campioni. Puoi scaricare il taccuino jupyter da qui e seguilo.
Primo, carichiamo i dati.
importa numpy come np importa panda come pd da sklearn.decomposition import PCA
df = pd.read_csv('winequality-red.csv')
df.head()
y = df.pop('qualità')
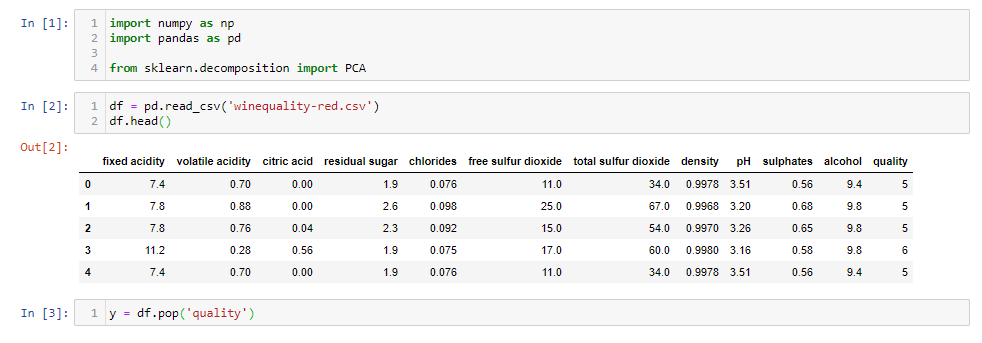
Dopo aver caricato i dati, eliminiamo la 'Qualità'’ del vino, poiché è la caratteristica dell'obiettivo. Ora scaleremo i dati perché in caso contrario, PCA non sarà in grado di trovare i componenti principali ottimali. Ad esempio. abbiamo una caratteristica in "metri"’ e un altro in "chilometri", la caratteristica con l'unità 'metro'’ avrà più varianza di "chilometri"’ (1 km = 1000 m), quindi PCA darà più importanza alla caratteristica con alta varianza . Quindi, facciamo la bilancia.
da sklearn.preprocessing import StandardScaler scalare = StandardScaler() df_scaled = pd.DataFrame(scalar.fit_transform(df), colonne=df.columns) df_scaled
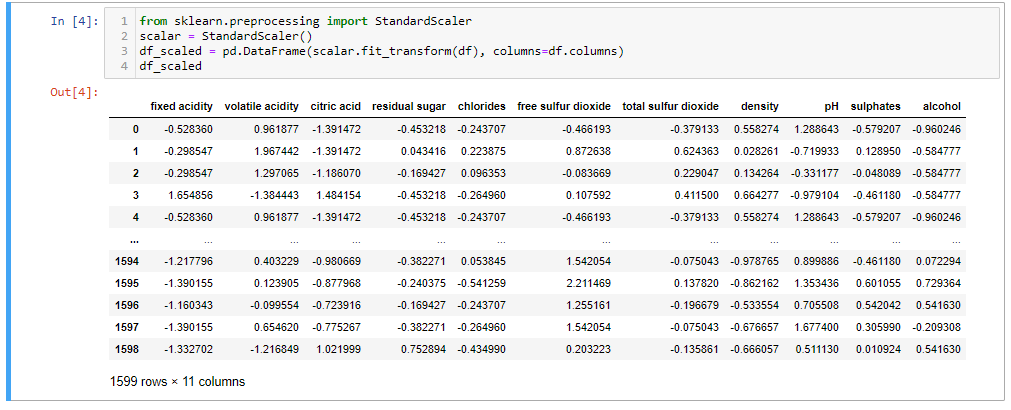
Ora noi
pca = PCA() df_pca = pd.DataFrame(pca.fit_transform(df_scaled)) df_pca
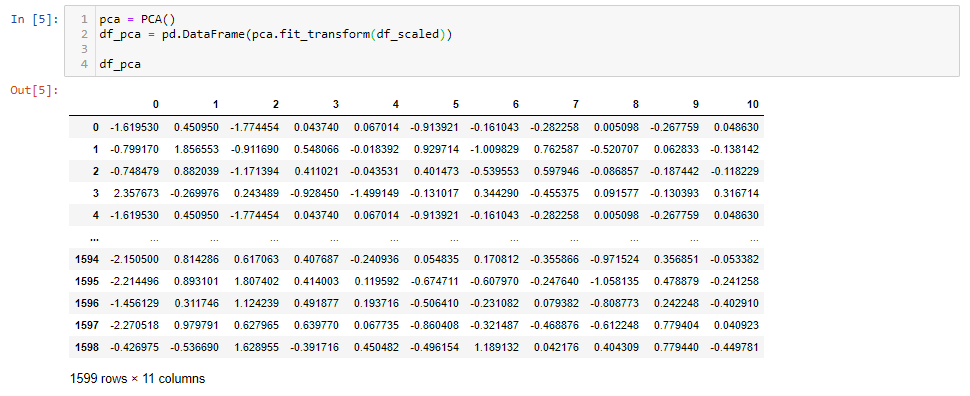
Dopo aver applicato PCA, noi abbiamo 11 componenti principali. È interessante vedere quanta varianza cattura ogni componente principale.
importa matplotlib.pyplot come plt
pd.DataFrame(pca.explained_variance_ratio_).trama.bar()
plt.legend('')
plt.xlabel("Componenti principali")
plt.ylabel("Varianza spiegata");
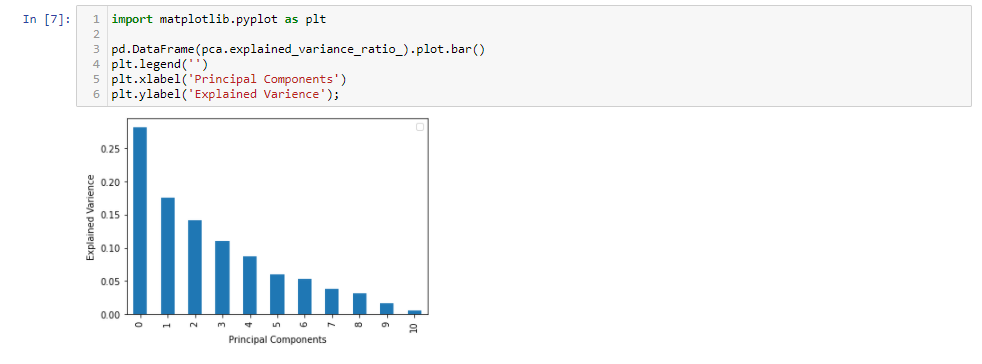
Il primo 5 i componenti principali catturano intorno al 80% della varianza, così possiamo sostituire il 11 caratteristiche originali (acidità, residuo zuccherino, cloruri, eccetera.) con il nuovo 5 caratteristiche che hanno 80% delle informazioni. Perciò, abbiamo ridotto il 11 dimensioni appena 5 dimensioni, mantenendo la maggior parte delle informazioni.
Differenza tra PCA, ICA e t-SNE
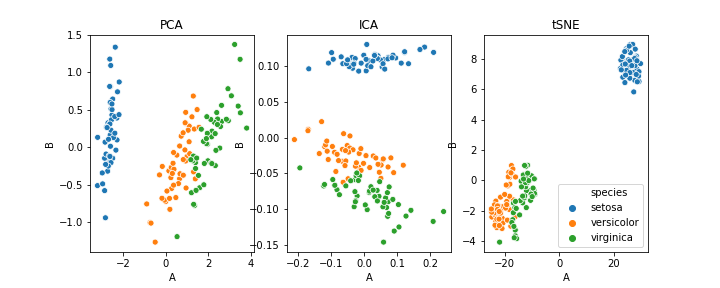
In che modo questo articolo si concentra sulle idee di base alla base della riduzione della dimensionalità e su come funziona la PCA, non entreremo nei dettagli, ma chi è interessato può passare Questo articolo.
In sintesi, PCA riduce la dimensionalità catturando la maggior parte della varianza. Ora, sarebbe entusiasta di applicare la PCA ai tuoi dati, ma prima, Voglio evidenziare alcuni degli svantaggi della PCA:
- Le variabili indipendenti diventano meno interpretabili
- La standardizzazione dei dati è un must prima della PCA
- Perdita di informazioni
Spero che troverai questo articolo informativo. Grazie!
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.






