Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
viene utilizzato per prevedere i valori futuri in base ai valori osservati in precedenza e uno dei migliori strumenti per l'analisi delle tendenze e la previsione futura.
Che cosa sono i dati delle serie temporali??
Viene registrato a intervalli di tempo regolari e l'ordine di questi punti dati è importante. Perciò, cualquier modelo predictivo basado en datos de series de tiempo tendrá el tiempo como variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... Indipendente. L'output di un modello sarebbe il valore previsto o il rango in un momento specifico.
Analisi delle serie temporali vs previsione delle serie temporali
Parliamo di una possibile confusione sull'analisi e la previsione delle serie temporali. La previsione delle serie temporali è un esempio di modellazione predittiva, mentre l'analisi delle serie temporali è una forma di modellazione descrittiva.
Per un nuovo investitore, la ricerca generale associata al mercato azionario o al mercato azionario non è sufficiente per prendere la decisione. La tendenza comune verso il mercato azionario tra la società è altamente rischiosa per gli investimenti, quindi la maggior parte delle persone non può prendere decisioni basate su tendenze comuni. La variación estacional y el flujo constante de cualquier indiceIl "Indice" È uno strumento fondamentale nei libri e nei documenti, che consente di individuare rapidamente le informazioni desiderate. In genere, Viene presentato all'inizio di un'opera e organizza i contenuti in modo gerarchico, compresi capitoli e sezioni. La sua corretta preparazione facilita la navigazione e migliora la comprensione del materiale, rendendolo una risorsa essenziale sia per gli studenti che per i professionisti in vari settori.... ayudarán a los inversores nuevos y existentes a comprender y tomar la decisión de invertir en el mercado de valores.
Per risolvere questo tipo di problemi, la previsione delle serie temporali è la tecnica migliore.
Borsa valori
I mercati azionari sono i luoghi in cui investitori individuali e istituzionali si incontrano per acquistare e vendere azioni in un luogo pubblico.. Oggi, questi scambi esistono come mercati elettronici.
Quella domanda e offerta aiutano a determinare il prezzo di ciascun titolo o i livelli ai quali i partecipanti al mercato azionario (investitori e commercianti) sono disposti a comprare o vendere.
Il concetto alla base del funzionamento del mercato azionario è abbastanza semplice.. Operando proprio come una casa d'aste, il mercato azionario consente ad acquirenti e venditori di negoziare prezzi ed effettuare transazioni.
Definizione di "stock"’
Un'azione o un'azione (conosciuto anche come “capitale” di un'azienda) è uno strumento finanziario che rappresenta la proprietà di una società
Apprendimento automatico in borsa
Il mercato azionario è molto imprevedibile, qualsiasi cambiamento geopolitico può influenzare l'andamento delle azioni nel mercato azionario, di recente abbiamo visto come il covid-19 ha influito sui prezzi delle azioni, quindi nei dati finanziari è molto difficile fare un'analisi di tendenza affidabile. . La forma más eficiente de resolver este tipo de problemas es con la ayuda del aprendizaje automático y el apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute....
In questo tutorial, risolveremo questo problema con il modello ARIMA.
Per conoscere la stagionalità, controlla il mio blog precedente. E per avere una conoscenza di base di ARIMA, Ti consiglio di leggere questo blog, esto lo ayudará a comprender mejor cómo funciona el análisis de series temporales.
Implementar la previsión del precio de las acciones
userò nsepy biblioteca para extraer los datos históricos de SBIN.
Importazioni
import os import warnings warnings.filterwarnings('ignorare') from pylab import rcParams rcParams['figura.figsize'] = 10, 6 from statsmodels.tsa.stattools import adfuller from statsmodels.tsa.seasonal import seasonal_decompose from statsmodels.tsa.arima_model import ARIMA from pmdarima.arima import auto_arima from sklearn.metrics import mean_squared_error, mean_absolute_error import math import numpy as np from nsepy import get_history from datetime import date import matplotlib.pyplot as plt import seaborn as sns import pandas as pd
Eseguire il codice seguente per estrarre i dati storici:
sbin = get_history(simbolo="SBIN ·",
inizio=data(2000,1,1),
fine=data(2020,11,1))
sbin.head()
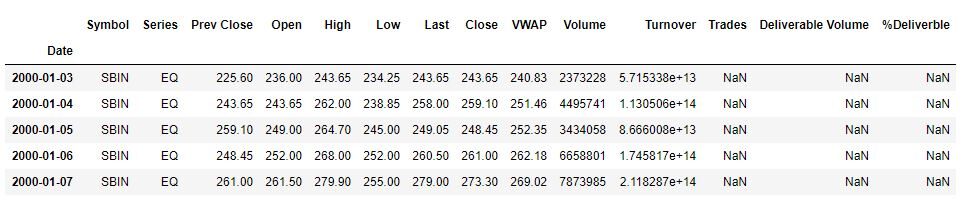
I dati mostrano il prezzo delle azioni di SBIN da 2020-1-1 a 2020-11-1. L'obiettivo è creare un modello che preveda
il prezzo di chiusura del titolo.
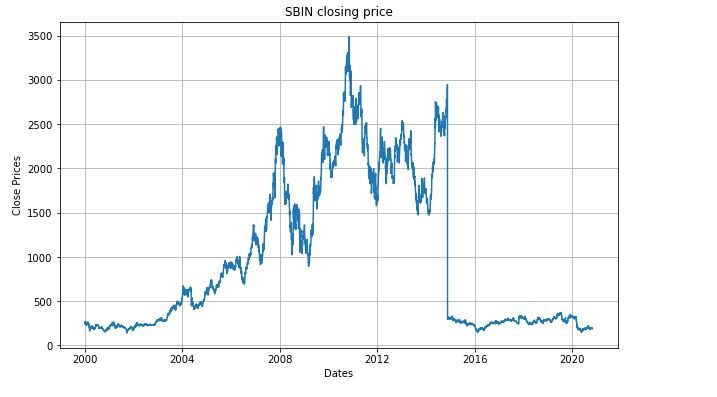
Creiamo una visualizzazione che mostri il prezzo di chiusura giornaliero del titolo.
plt.figure(figsize=(10,6))
plt.grid(Vero)
plt.xlabel('Date')
plt.ylabel("Chiudi prezzi")
plt.trama(sbin['Chiudere'])
plt.titolo('Prezzo di chiusura SBIN')
plt.mostra()
plt.figure(figsize=(10,6))
df_close = sbin['Chiudere']
df_close.plot(stile="K.")
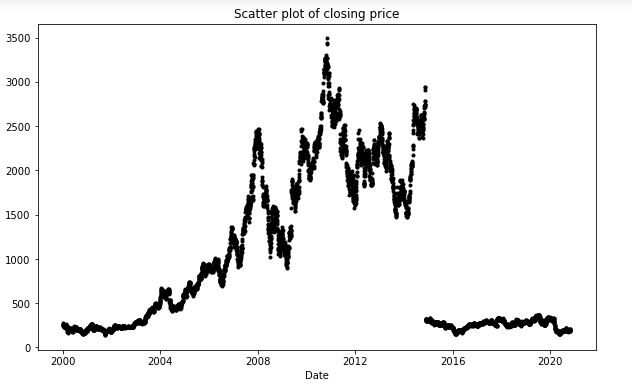
plt.titolo('Grafico a dispersioneUn diagrama de dispersión es una representación gráfica que muestra la relación entre dos variables. Cada punto en el gráfico corresponde a un par de valores, lo que permite identificar patrones, tendencias o correlaciones. Esta herramienta es útil en diversas disciplinas, como la estadística y la investigación científica, ya que facilita el análisis visual de datos y la comprensión de la relación entre los elementos estudiados.... of closing price')
plt.mostra()
plt.figure(figsize=(10,6))
df_close = sbin['Chiudere']
df_close.plot(stile="K.",bambino = 'storico')
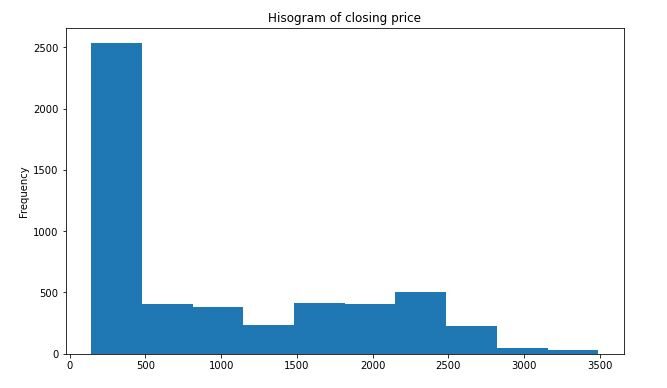
plt.titolo('Isogramma del prezzo di chiusura')
plt.mostra()
Primo, dobbiamo verificare se una serie è stazionaria o meno perché l'analisi delle serie temporali funziona solo con dati stazionari.
Prova di stazionarietà:
Per identificare la natura dei dati, Useremo il ipotesi nullaL'ipotesi nulla è un concetto fondamentale in statistica che stabilisce un'affermazione iniziale su un parametro di popolazione. Il suo scopo è quello di essere testato e, se confutato, ci permette di accettare l'ipotesi alternativa. Questo approccio è essenziale nella ricerca scientifica, in quanto fornisce un quadro di riferimento per valutare le prove empiriche e prendere decisioni basate sui dati. La sua formulazione e analisi sono cruciali negli studi statistici.....
H0: L'ipotesi nulla: È un'affermazione sulla popolazione che si crede sia vera o usata per fare un'argomentazione a meno che non si possa dimostrare che è errata oltre ogni ragionevole dubbio.
H1: L'ipotesi alternativa: È un'affermazione sulla popolazione che contraddice h0 e cosa concludiamo quando rifiutiamo h0.
#come: non è stazionario
# H1: è fermato
Se non rifiutiamo l'ipotesi nulla, possiamo dire che la serie è non stazionaria. Ciò significa che la serie può essere lineare.
Se sia la deviazione standard che la media sono linee piatte (media costante e varianza costante), la serie diventa stazionaria.
da statsmodels.tsa.stattools import adfuller
def test_stazionarietà(serie temporali):
#Determinazione delle statistiche di rotazione
rolmean = timeseries.rolling(12).Significare()
rolstd = timeseries.rolling(12).standard()
#Statistiche di scorrimento della trama:
plt.trama(serie temporali, colore="giallo",etichetta="Originale")
plt.trama(rolmean, colore="rosso", etichetta="Media rotante")
plt.trama(rolstd, colore="Nero", etichetta="Standard di rotolamento")
plt.legend(loc ="migliore")
plt.titolo("Media mobile e deviazione standard")
plt.mostra(blocco=Falso)
Stampa("Risultati del test dickey fuller")
adft = adfuller(serie temporali,autolag = 'AIC')
# l'output per dft ci darà senza definire quali sono i valori.
#quindi scriviamo manualmente quali valori spiega usando un ciclo for
output = pd.Serie(adft[0:4],indice=["Statistiche di prova",'valore p','No. di ritardi utilizzati',"Numero di osservazioni utilizzate"])
per chiave,valori in adft[4].Oggetti():
produzione['valore critico (%S)'%chiave] = valori
Stampa(produzione)
test_stazionarietà(sbin['Chiudere'])
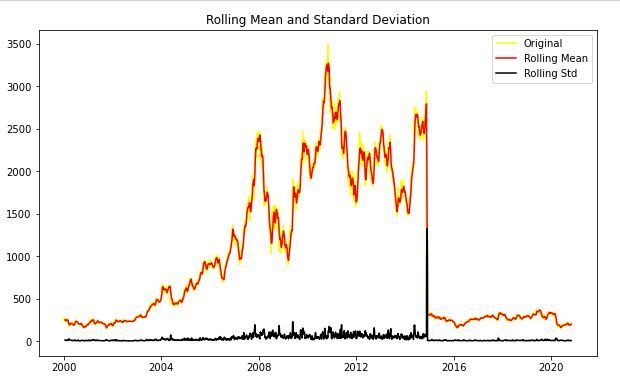
Dopo aver analizzato il grafico sopra, possiamo vedere la media crescente e la deviazione standard e quindi la nostra serie non è stazionaria.
Results of dickey fuller test
Test Statistics -1.914523
valore p 0.325260
No. numero di ritardi utilizzati 3.000000
Numero di osservazioni utilizzate 5183.000000
valore critico (1%) -3.431612
valore critico (5%) -2.862098
valore critico (10%) -2.567067
dtype: float64Vemos que el valor p es mayor que 0.05 por lo que no podemos rechazar el Ipotesi nulla. Cosa c'è di più, las estadísticas de la prueba son mayores que los valores críticos. por lo que los datos no son estacionarios.
Para el análisis de series de tiempo, separamos Tendencia y Estacionalidad de las series de tiempo.
risultato = seasonal_decompose(df_close, modello="moltiplicativo", frequenza = 30) fig = plt.figure() fig = risultato.trama() fig.set_size_inches(16, 9)
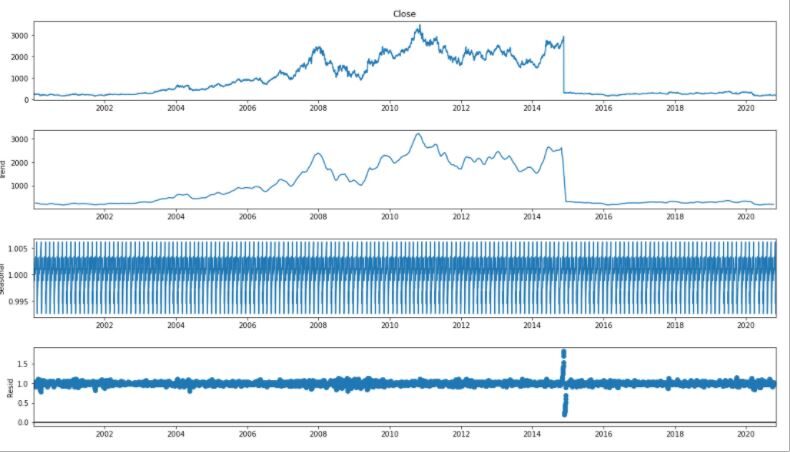
from pylab import rcParams
rcParams['figura.figsize'] = 10, 6
df_log = np.log(sbin['Chiudere'])
Moving_avg = df_log.rolling(12).Significare()
std_dev = df_log.rolling(12).standard()
plt.legend(loc ="migliore")
plt.titolo("Media mobile")
plt.trama(std_dev, colore ="Nero", etichetta = "Deviazione standard")
plt.trama(Moving_avg, colore="rosso", etichetta = "Significare")
plt.legend()
plt.mostra()
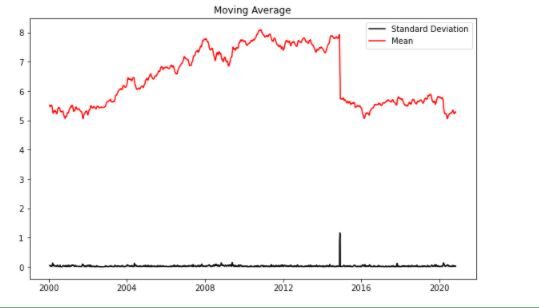
Ora creeremo un modello ARIMA e lo addestreremo con il prezzo di chiusura del titolo nei dati del treno. Así que dividamos los datos en addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.... y conjunto de prueba y visualícelos.
train_data, test_data = df_log[3:int(len(df_log)*0.9)], df_log[int(len(df_log)*0.9):]
plt.figure(figsize=(10,6))
plt.grid(Vero)
plt.xlabel('Date')
plt.ylabel("Prezzi di chiusura")
plt.trama(df_log, 'verde', etichetta="Dati del treno")
plt.trama(dati di test, 'blu', etichetta="Dati di test")
plt.legend()
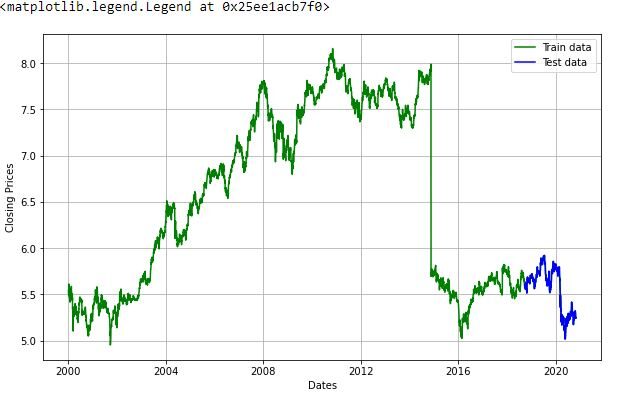
model_autoARIMA = auto_arima(train_data, start_p=0, start_q=0, test="Adf", # usa adftest per trovare la 'd' ottimale max_p=3, max_q=3, # massimo p e q m=1, # frequenza delle serie d=Nessuno, # lascia che il modello determini 'd' stagionale=Falso, # Nessuna stagionalità start_P=0, D=0, trace=Vero, error_action='ignora', sopprimere_avvertimenti=Vero, stepwise=Vero) Stampa(model_autoARIMA.sommario())
Performing stepwise search to minimize aic ARIMA(0,1,0)(0,0,0)[0] intercettare : AIC=-16607,561, Time=2.19 sec ARIMA(1,1,0)(0,0,0)[0] intercettare : AIC=-16607,961, Time=0.95 sec ARIMA(0,1,1)(0,0,0)[0] intercettare : AIC=-16608,035, Time=2.27 sec ARIMA(0,1,0)(0,0,0)[0] : AIC=-16609,560, Time=0.39 sec ARIMA(1,1,1)(0,0,0)[0] intercettare : AIC=-16606,477, Time=2.77 sec Best model: ARIMA(0,1,0)(0,0,0)[0] Tempo di adattamento totale: 9.079 seconds SARIMAX Results ============================================================================== Dep. Variabile: y No. Osservazioni: 4665 Modello: SARIMAX(0, 1, 0) Probabilità del registro 8305.780 Data: mar, 24 Nov 2020 AIC -16609.560 Ore: 20:08:50 BIC -16603.113 Campione: 0 HQIC -16607.293 - 4665 Tipo di covarianza: opg ============================================================================== coef std err z P>|Insieme a| [0.025 0.975] ------------------------------------------------------------------------------ sigma2 · 0.0017 1.06e-06 1566.660 0.000 0.002 0.002 =================================================================================== Ljung-Box (Q): 24.41 Jarque-Bera (JB ·): 859838819.58 Prob(Q): 0.98 Prob(JB ·): 0.00 Eteroskedasticità (h): 7.16 Inclinazione: -37.54 Prob(h) (bilaterale): 0.00 Kurtosi: 2105.12 ===================================================================================
model_autoARIMA.plot_diagnostics(figsize=(15,8)) plt.mostra()
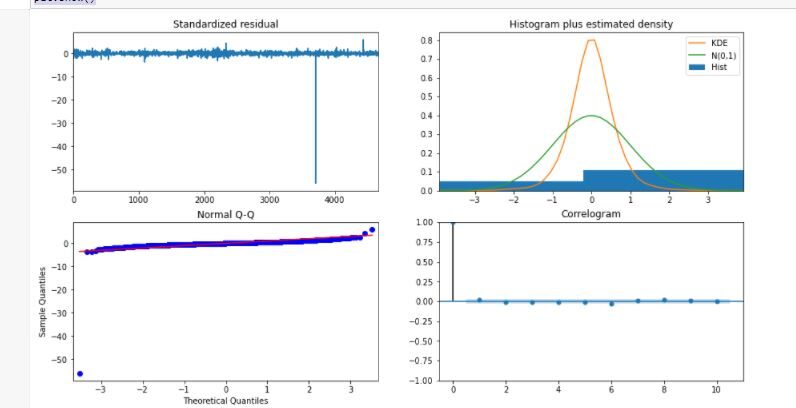
modello = ARIMA(train_data, ordine=(3, 1, 2)) montato = model.fit(disp=-1) Stampa(adattato.sommario())
ARIMA Model Results ============================================================================== Dep. Variabile: D.Chiudi No. Osservazioni: 4664 Modello: ARIMA(3, 1, 2) Probabilità del registro 8309.178 Metodo: css-mle S.D.. di innovazioni 0.041 Data: mar, 24 Nov 2020 AIC -16604.355 Ore: 20:09:37 BIC -16559.222 Campione: 1 HQIC -16588.481 ================================================================================= coef std err z P>|Insieme a| [0.025 0.975] --------------------------------------------------------------------------------- const 8.761e-06 0.001 0.015 0.988 -0.001 0.001 voler. L1. D.Chiudi 1.3689 0.251 5.460 0.000 0.877 1.860 voler. l2. D.Chiudi -0.7118 0.277 -2.567 0.010 -1.255 -0.168 voler. l3. D.Chiudi 0.0094 0.021 0.445 0.657 -0.032 0.051 Me. L1. D.Chiudi -1.3468 0.250 -5.382 0.000 -1.837 -0.856 Me. l2. D.Chiudi 0.6738 0.282 2.391 0.017 0.122 1.226 Roots ============================================================================= Real Imaginary Modulus Frequency ----------------------------------------------------------------------------- AR.1 · 0.9772 -0.6979J 1.2008 -0.0987 AR.2 · 0.9772 +0.6979J 1.2008 0.0987 AR.3 · 74.0622 -0.0000J 74.0622 -0.0000 MA.1 · 0.9994 -0.6966J 1.2183 -0.0969 MA.2 · 0.9994 +0.6966J 1.2183 0.0969 -----------------------------------------------------------------------------
# Forecast
fc, se, conf = fitted.forecast(519, alfa=0,05) # 95% fiduciafc_series = pd.Serie(fc, index=test_data.index)
serie_inferiore = pd.Serie(conf[:, 0], index=test_data.index)
serie_superiore = pd.Serie(conf[:, 1], index=test_data.index)
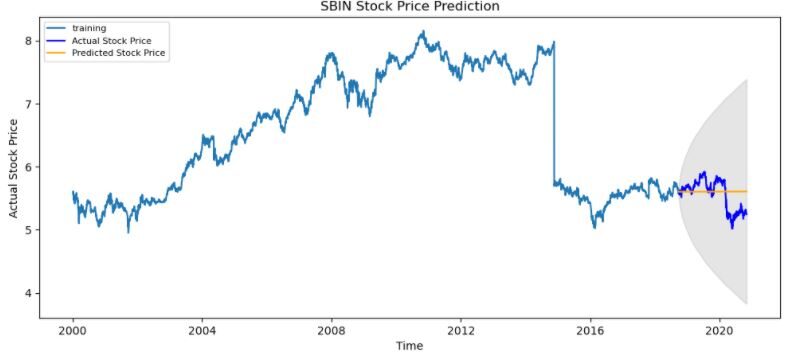
plt.figure(figsize=(12,5), dpi=100)
plt.trama(train_data, etichetta="addestramento")
plt.trama(dati di test, colore="blu", etichetta="Prezzo effettivo delle azioni")
plt.trama(fc_series, colore="arancia",etichetta="Prezzo delle azioni previsto")
plt.fill_between(serie_inferiore.indice, serie_inferiore, serie_superiore,
colore="K", alfa=.10)
plt.titolo("Previsione del prezzo delle azioni SBIN")
plt.xlabel('Tempo')
plt.ylabel("Prezzo effettivo delle azioni")
plt.legend(loc ="superiore sinistro", dimensione del carattere=8)
plt.mostra()
conclusione
La previsione delle serie temporali è davvero utile quando dobbiamo prendere decisioni future o dobbiamo fare analisi, possiamo farlo rapidamente usando ARIMA, ci sono molti altri modelli da cui possiamo fare previsioni di serie temporali, ma ARIMA è davvero facile da capire.
Spero che questo articolo ti aiuti e ti faccia risparmiare una buona quantità di tempo.. Fatemi sapere se avete suggerimenti..
FELICE CODIFICA.
Prabhat Pathak (Profilo LinkedIn) è un analista senior e un appassionato di innovazione.
