introduzione
In questo articolo, esamineremo il popolare set di dati del Titanic e proveremo a prevedere se una persona è sopravvissuta al relitto. Puoi ottenere questo set di dati da Kaggle, collegato qui. Questo articolo si concentrerà su come pensare a questi progetti, più che nella realizzazione. Molti principianti sono confusi su come iniziare, quando finire e tutto il resto, Spero che questo articolo ti serva da manuale per principianti.. Ti suggerisco di praticare il progetto in Kaggle.
L'obiettivo: prevedere se un passeggero è sopravvissuto o meno. 0 per non sopravvivere, 1 per sopravvivere.
Descrizione dei dati
In questo articolo, faremo un'analisi dei dati di base, poi un po' di ingegneria delle funzionalità e, alla fine, useremo alcuni dei modelli popolari per la previsione. Cominciamo.
Analisi dei dati
passo 1: Importazione di librerie di base
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inlinepasso 2: leggere i dati
formazione = pd.read_csv('/kaggle/input/titanic/treno.csv')
test = pd.read_csv('/kaggle/input/titanic/test.csv')addestramento['train_test'] = 1
test['train_test'] = 0
test['Sopravvissuto'] = np.NaN
all_data = pd.concat([addestramento,test])all_data.columns
passo 3: esplorazione dei dati
In questa sezione, cercheremo di estrarre insight dai dati e familiarizzare con essi al fine di creare modelli più efficienti.
training.info()
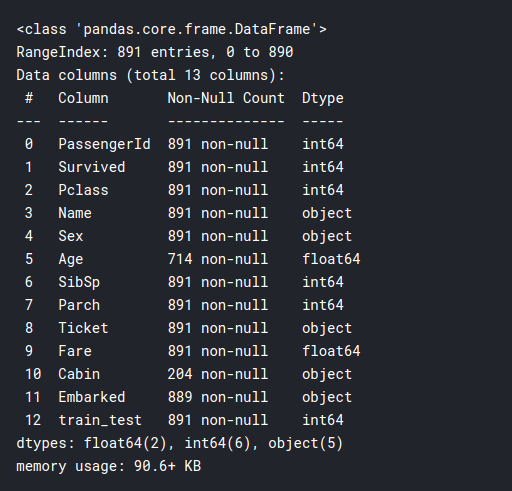
training.descrivere()
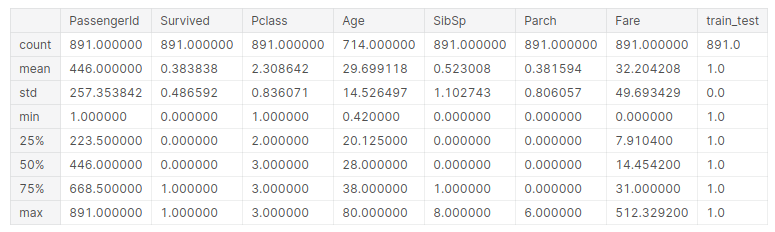
# seperate the data into numeric and categorical
df_num = training[['Età','SibSp','Rispetto',"Tariffa"]]
df_cat = allenamento[['Sopravvissuto','classe','Sesso','Biglietto','Cabina',"Imbarcato"]]Ora graficiamo i dati numerici:
per io in df_num.columns:
plt.hist(df_num[io])
plt.titolo(io)
plt.mostra()
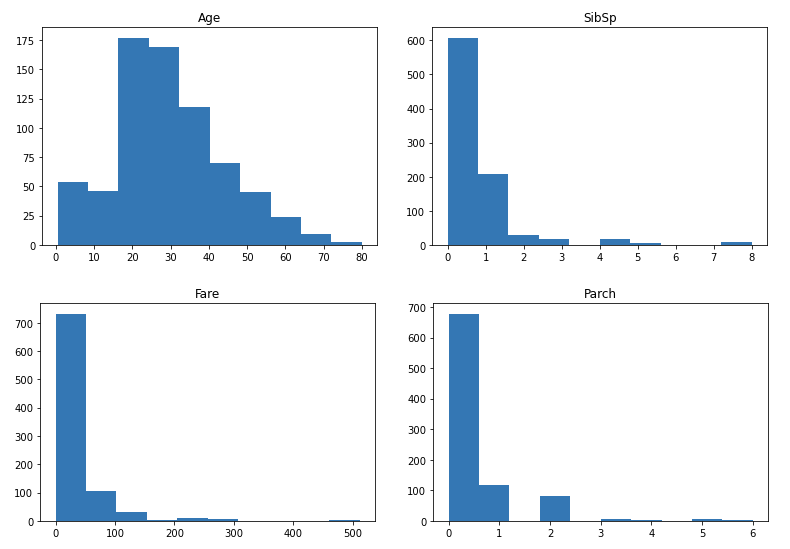
Quindi, come potete vedere, la maggior parte delle distribuzioni sono sparse, tranne l'età, è abbastanza normalizzato. Potremmo considerare di normalizzarli in seguito. Prossimo, trazamos un mappa di caloreun "mappa di calore" è una rappresentazione grafica che utilizza i colori per mostrare la densità dei dati in un'area specifica. Comunemente usato nell'analisi dei dati, Marketing e studi comportamentali, Questo tipo di visualizzazione consente di identificare rapidamente modelli e tendenze. Attraverso variazioni cromatiche, Le mappe di calore facilitano l'interpretazione di grandi volumi di informazioni, aiutando a prendere decisioni informate.... de correlación entre las columnas numéricas:
sns.heatmap(df_num.corr())
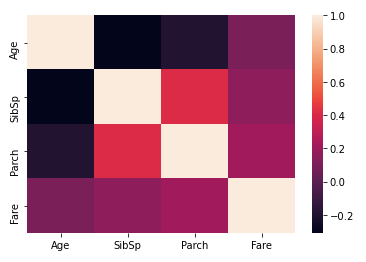
Qui possiamo vedere che Parch e SibSp hanno una correlazione maggiore, il che generalmente ha senso in quanto i genitori hanno maggiori probabilità di viaggiare con i loro più figli e i coniugi tendono a viaggiare insieme. Prossimo, confrontiamo i tassi di sopravvivenza tra variabili numeriche. Questo potrebbe rivelare alcune idee interessanti:
pd.pivot_table(addestramento, indice = 'Sopravvissuto', valori = ['Età','SibSp','Rispetto',"Tariffa"])
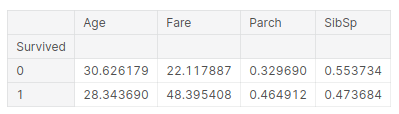
L'inferenza che possiamo trarre da questa tabella è:
- L'età media dei sopravvissuti è 28 anni, quindi i giovani tendono a sopravvivere più a lungo.
- Le persone che pagavano tariffe più alte avevano maggiori probabilità di sopravvivere, più del doppio. Queste potrebbero essere le persone che viaggiano in prima classe. Ecco come sono sopravvissuti i ricchi, che è una storia triste su questo palco.
- Nella terza colonna, se hai i genitori, ha maggiori possibilità di sopravvivere. Quindi, i genitori avrebbero potuto salvare i bambini prima di loro stessi, spiegando così le tariffe
- E se sei un bambino e hai fratelli, hai meno possibilità di sopravvivere.
Ora facciamo qualcosa di simile con le nostre variabili categoriali:
per io in df_cat.columns:
sns.barplot(df_cat[io].value_counts().indice,df_cat[io].value_counts()).set_title(io)
plt.mostra()
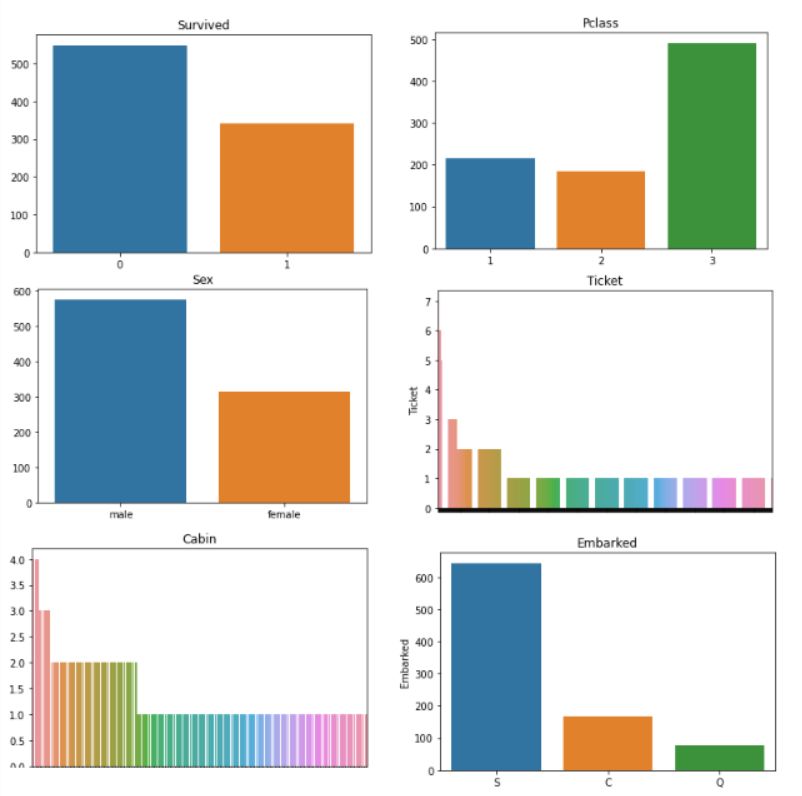
La grafica del biglietto e della cabina sembra molto disordinata, Potrebbe essere necessario progettarli! Oltre a quello, il resto dei grafici ce lo dicono:
- Sopravvissuto: la maggior parte delle persone è morta nel naufragio, solo alcuni 300 le persone sono sopravvissute.
- Pclass: La maggior parte delle persone che viaggiavano aveva biglietti di 3a classe.
- Sesso: c'erano più uomini che donne a bordo della nave, circa il doppio della quantità.
- Imbarcato: La maggior parte dei passeggeri è salita a bordo della nave da Southampton.
Ahora haremos algo similar a la tabella dinamicaLa tabla dinámica es una herramienta poderosa en programas de hoja de cálculo, como Microsoft Excel y Google Sheets. Permite resumir, analizar y visualizar grandes volúmenes de datos de manera eficiente. A través de su interfaz intuitiva, los usuarios pueden reorganizar la información, aplicar filtros y crear informes personalizados, facilitando la toma de decisiones informadas en diversos contextos, desde el ámbito empresarial hasta la investigación académica.... anteriore, ma con le nostre variabili categoriali, y las compararemos con nuestra variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... dipendente, e se le persone sopravvivessero?:
Stampa(pd.pivot_table(addestramento, indice = 'Sopravvissuto', colonne="Pclass",
valori="Biglietto" ,aggfunc="contare"))
Stampa()
Stampa(pd.pivot_table(addestramento, indice = 'Sopravvissuto', colonne="Sesso",
valori="Biglietto" ,aggfunc="contare"))
Stampa()
Stampa(pd.pivot_table(addestramento, indice = 'Sopravvissuto', colonne="Imbarcato",
valori="Biglietto" ,aggfunc="contare"))
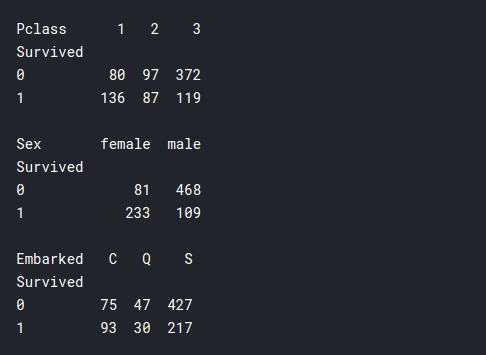
- Pclass: Qui possiamo vedere che molte più persone della prima classe sono sopravvissute rispetto alla seconda o terza classe., anche se il numero totale di passeggeri in Prima classe era molto inferiore a quello in Terza classe. Perciò, qui viene confermata la nostra precedente supposizione che i ricchi sopravvivessero, cosa potrebbe essere rilevante per la costruzione di modelli.
- Sesso: la maggior parte delle donne sopravvisse e la maggior parte degli uomini morì nel naufragio. Perciò, sembra che il detto “Prima donna e bambini” si applica davvero in questo scenario.
- Imbarcato: Questo non sembra molto rilevante, forse se qualcuno fosse di “Cherburgo"Avevo maggiori possibilità di sopravvivere.
passo 4: Ingegneria delle funzioni
Abbiamo visto che il nostro biglietto e cabina i dati non hanno molto senso per noi, e questo potrebbe ostacolare le prestazioni del nostro modello, quindi dobbiamo semplificare alcuni di questi dati con l'ingegneria delle funzioni.
Se guardiamo i dati reali della cabina, vediamo che in fondo c'è una lettera e poi un numero. Le lettere possono significare che tipo di cabina è, dove sei sulla nave, su quale piano, per che classe è, eccetera. E i numeri possono significare il numero della cabina. Per prima cosa dividiamoli in cabine individuali e vediamo se qualcuno aveva più di una cabina..
df_cat.Cabin
training['cabin_multiple'] = formazione. Cabin.apply(lambda x: 0 se pd.isna(X)
else len(x.split(' ')))
addestramento['cabin_multiple'].value_counts()
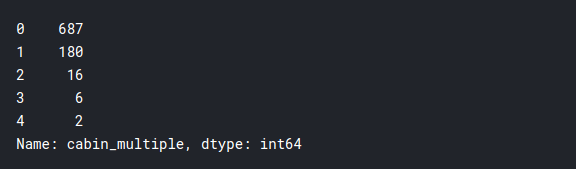
Sembra che la stragrande maggioranza non avesse cabine individuali, e solo poche persone avevano più di una cabina. Ora vediamo se i tassi di sopravvivenza dipendono da questo.:
pd.pivot_table(addestramento, indice = 'Sopravvissuto', colonne="cabin_multiple",
valori="Biglietto" ,aggfunc="contare")
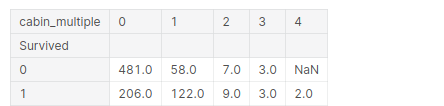
Prossimo, vediamo la grafia effettiva della cabina in cui si trovavano. Perciò, ci si potrebbe aspettare che le cabine con la stessa lettera si trovino all'incirca nelle stesse posizioni o sugli stessi piani e, logicamente, se una cabina era vicino a scialuppe di salvataggio, aveva maggiori possibilità di sopravvivere. Diamo un'occhiata a questo.:
# n sta per null # in this case we will treat null values like it's own category training['cabin_adv'] = formazione. Cabin.apply(lambda x: str(X)[0]) #comparing survival rates by cabin print(training.cabin_adv.value_counts()) pd.pivot_table(addestramento,index='Sopravvissuto',colonne="cabin_adv", valori="Nome", aggfunc="contare")
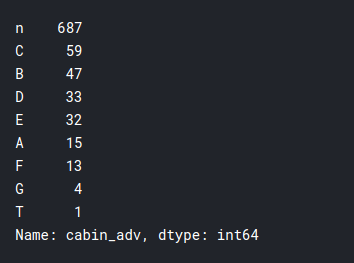
Ho fatto un po 'di ingegneria futura nel biglietto e non ha prodotto molte conoscenze importanti, che non sappiamo ancora, quindi salterò quella parte per mantenere l'articolo conciso. Divideremo semplicemente i biglietti in numerici e non numerici per un uso efficiente:
addestramento['numeric_ticket'] = formazione. Ticket.apply(lambda x: 1 se x.isnumerico() altro 0)
addestramento['ticket_letters'] = formazione. Ticket.apply(lambda x: ''.join(x.split(' ')[:-1])
.sostituire('.','').sostituire('/','')
.inferiore() se len(x.split(' ')[:-1]) >0 altro 0)Un'altra cosa interessante che possiamo osservare è il titolo dei singoli passeggeri. E se ha avuto un ruolo nell'ottenere loro un posto nelle scialuppe di salvataggio.
training.Nome.testa(50)
addestramento['nome_titolo'] = training.Nome.applica(lambda x: x.split(',')[1]
.diviso('.')[0].striscia())
addestramento['nome_titolo'].value_counts()
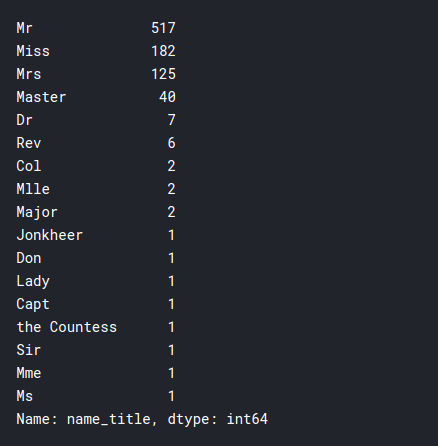
Come potete vedere, la nave è stata abbordata da persone di molte classi diverse, questo potrebbe essere utile nel nostro modello.
passo 5: pre-elaborazione dei dati per il modello
In questo segmento, prepariamo i nostri dati per i modelli. Gli obiettivi che dobbiamo raggiungere sono elencati di seguito:
- Rimuovi i valori null dalla colonna Spedito
- Includi solo dati rilevanti
- Trasforma categoricamente tutti i dati, usando qualcosa chiamato trasformatore.
- Calcolo dei dati con trend centrali per età e tasso.
- Normalizza il Vota colonna per avere una distribuzione più normale.
- utilizzando dati di scala standard 0-1
passo 6: Implementazione del modello
Aquí simplemente implementaremos los diversos modelos con parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... predeterminados y veremos cuál produce el mejor resultado. I modelli possono essere ulteriormente regolati per prestazioni migliori, ma non rientrano nell'ambito di questo articolo. I modelli che eseguiremo sono:
- Regressione logistica
- K Il vicino più vicino
- Classificatore vettoriale di supporto
Primo, importiamo i modelli necessari
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC1) Regressione logistica
lr = LogisticRegression(max_iter = 2000) cv = cross_val_score(lr,X_train_scaled,y_train,cv=5) Stampa(CV) Stampa(cv.mean())
2) K Il vicino più vicino
knn = KNeighborsClassifier() cv = cross_val_score(knn,X_train_scaled,y_train,cv=5) Stampa(CV) Stampa(cv.mean())
3) Classificatore vettoriale di supporto
svc = SVC(probabilità = Vero) cv = cross_val_score(Svc,X_train_scaled,y_train,cv=5) Stampa(CV) Stampa(cv.mean())
Perciò, la precisione dei modelli è:
- Regressione logistica: 82,2%
- K Il vicino più vicino: 81,4%
- SVC: 83,3%
Come potete vedere, otteniamo una precisione decente con tutti i nostri modelli, ma il migliore è SVC. E pronto, ecco come hai completato il tuo primo progetto di data science! Sebbene si possa fare molto di più per ottenere risultati migliori, questo è più che sufficiente per iniziare e vedere come pensi come uno scienziato dei dati. Spero che questo tutorial ti abbia aiutato, Mi sono divertito molto a realizzare il progetto da solo e spero che piaccia anche a voi. Salute!!
