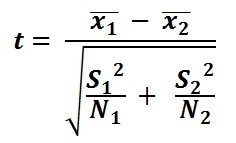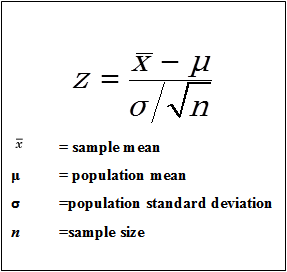Verifica di ipotesi | Prove parametriche e non parametriche

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

introduzione

Il test di ipotesi è uno dei concetti più importanti nelle statistiche ampiamente utilizzato da Statistiche, Ingegneri dell'apprendimento automatico, e Scienziati dei dati.

Nel test di ipotesi, I test statistici vengono utilizzati per verificare se il ipotesi nullaL'ipotesi nulla è un concetto fondamentale in statistica che stabilisce un'affermazione iniziale su un parametro di popolazione. Il suo scopo è quello di essere testato e, se confutato, ci permette di accettare l'ipotesi alternativa. Questo approccio è essenziale nella ricerca scientifica, in quanto fornisce un quadro di riferimento per valutare le prove empiriche e prendere decisioni basate sui dati. La sua formulazione e analisi sono cruciali negli studi statistici.... viene rifiutato o non rifiutato. Sono Test statistici assumere un nullo ipotesi nessuna relazione o nessuna differenza tra i gruppi.

Quindi, in questo articolo, discuteremo il test statistico per il test di ipotesi, compresi i test parametrici e non parametrici.

Sommario

1. Cosa sono i test parametrici?

2. Cosa sono i test non parametrici?

3. Test parametrici per la verifica di ipotesi

• t-test
• Prova Z
• Prova F
• ANOVA

4. Test non parametrici per la verifica di ipotesi

• Chi al quadrato
• Test U di Mann-Whitney
• Test di Kruskal-Wallis H

Cominciamo,

prove parametriche

El principio básico detrás de las pruebas paramétricas es que tenemos un conjunto fijo de parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... que se utilizan para determinar un modelo probabilístico que también se puede utilizar en Machine Learning.

I test parametrici sono quei test per i quali abbiamo una conoscenza preliminare della distribuzione della popolazione. (vale a dire, normale), o se no, possiamo facilmente approssimarlo a una distribuzione normale, cosa possibile con l'aiuto del teorema del limite centrale.

I parametri per l'utilizzo della distribuzione normale sono:

Finalmente, la classificazione di un test come parametrico dipende interamente dalle ipotesi della popolazione. Sono disponibili molti test parametrici, alcuni dei quali sono i seguenti:

• Trovare l'intervallo di confidenza per la popolazione significa con l'aiuto della deviazione standard nota.
• Determinare l'intervallo di confidenza per la media della popolazione insieme alla deviazione standard sconosciuta.
• Trovare l'intervallo di confidenza per la varianza della popolazione.
• Trovare l'intervallo di confidenza per la differenza di due medie, con un valore di deviazione standard sconosciuto.

Test non parametrici

Nei test non parametrici, non facciamo alcuna ipotesi sui parametri per la data popolazione o la popolazione che stiamo studiando. Infatti, questi test non dipendono dalla popolazione.
Perciò, nessun set di parametri fisso disponibile, e non c'è distribuzione (distribuzione normale, eccetera.) di qualsiasi tipo disponibile per l'uso.

Questo è anche il motivo per cui vengono chiamati anche test non parametrici test senza distribuzione.
Attualmente, i test non parametrici stanno guadagnando popolarità e un impatto influente, alcune delle ragioni dietro questa fama sono:

• Il motivo principale è che non è necessario essere educati quando si utilizzano i test parametrici..
• La seconda ragione è che non è necessario fare ipotesi sulla popolazione data (la presa) su cui stiamo facendo l'analisi.
• La maggior parte dei test non parametrici disponibili sono anche molto facili da applicare e da comprendere, vale a dire, la complessità è molto bassa.

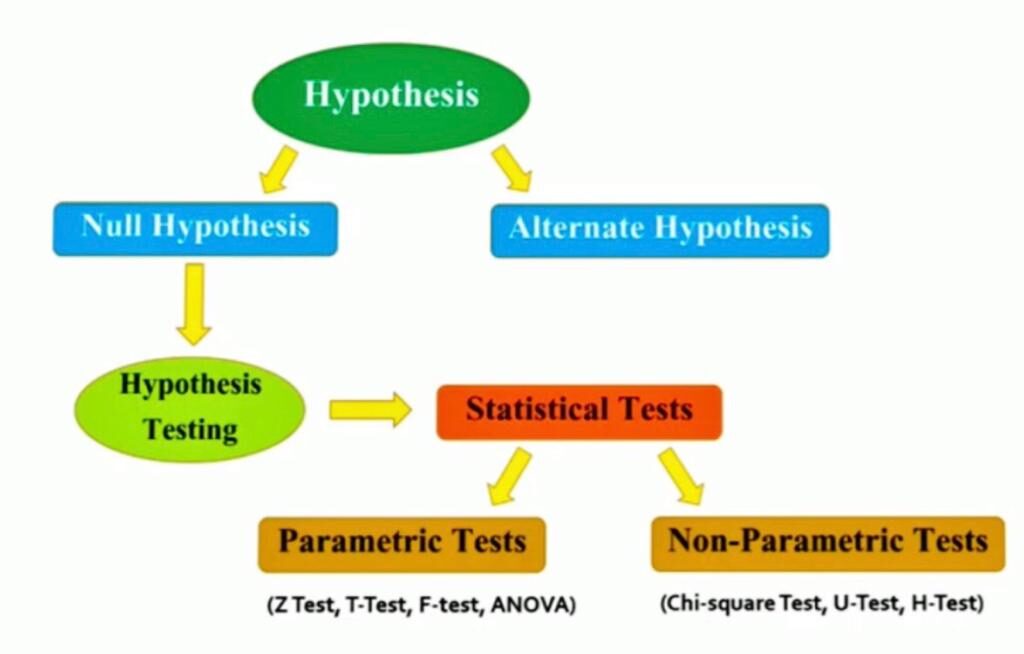
Fonte immagine: Google Immagini

Prova T

1. È un test parametrico di verifica di ipotesi basato su Distribuzione t di Student.

2. Essenzialmente, si tratta di testare la significatività della differenza dei valori medi quando la dimensione del campione è piccola (vale a dire, meno di 30) e quando la deviazione standard della popolazione non è disponibile.

3. Presupposti di questa prova:

• La distribuzione della popolazione è normale e
• I campioni sono casuali e indipendenti..
• La dimensione del campione è piccola.
• Deviazione standard della popolazione sconosciuta.

4. Il test "U".’ Mann-Whitney è una controparte non parametrica del test t.

Un t-test può essere:

Un test T campione: Confronta una media campionaria con la media della popolazione.

dove,

X è la media campionaria

S è la deviazione standard del campione

Nord è la dimensione del campione

μ è la media della popolazione

T-test a due campioni: Confronta le medie di due diversi campioni.

dove,

X₁ è la media campionaria del primo gruppo

X₂ è la media campionaria del secondo gruppo

S₁ è la deviazione standard del campione 1

S₂ è la deviazione standard del campione 2

Nord è la dimensione del campione

conclusione:

• Se il valore della statistica del test è maggiore del valore della tabella -> rifiutare l'ipotesi nulla.
• Se il valore della statistica del test è inferiore al valore della tabella -> Non rifiutare l'ipotesi nulla.

Prova Z

1. È un test parametrico di verifica di ipotesi.

2. Viene utilizzato per determinare se le medie sono diverse quando la varianza della popolazione è nota e la dimensione del campione è ampia. (vale a dire, più grande di 30).

3. Presupposti di questa prova:

• La distribuzione della popolazione è normale.
• I campioni sono casuali e indipendenti..
• La dimensione del campione è grande.
• La deviazione standard della popolazione è nota..

Può essere un test Z:

Un test Z campione: Confronta una media campionaria con la media della popolazione.

Fonte immagine: Google Immagini

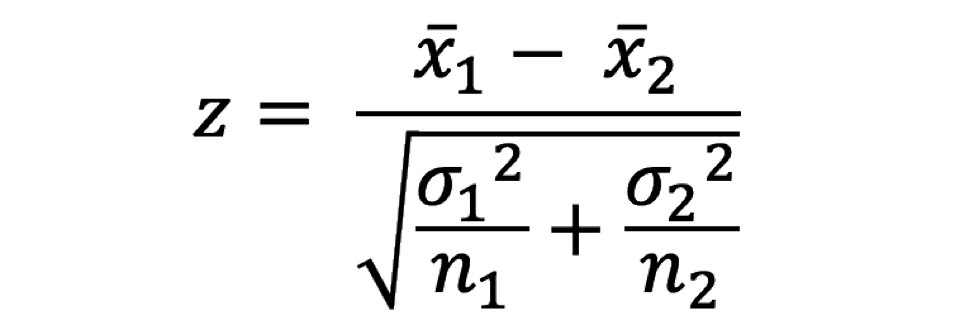
Test Z a due campioni: Confronta le medie di due diversi campioni.

dove,

X₁ è la media campionaria del primo gruppo

X₂ è la media campionaria del secondo gruppo

?₁ è la deviazione standard della popolazione 1

?₂ è la deviazione standard della popolazione 2

Nord è la dimensione del campione

Prova F

1. È un test parametrico di verifica di ipotesi basato su Distribuzione Snedecor F.

2. È un test per l'ipotesi nulla che due popolazioni normali abbiano la stessa varianza..

3. Un test F è considerato un confronto dell'uguaglianza delle varianze campionarie.

4. La statistica F è semplicemente un rapporto di due varianze.

5. È calcolato come:

F = s₁²/S₂²

6. Modificando la varianza nella relazione, il test F è diventato un test molto flessibile. Quindi può essere utilizzato per:

• Verifica la significatività complessiva per un modello di regressione.
• Confronta le impostazioni di diversi modelli e
• verificare l'uguaglianza dei mezzi.

7. Presupposti di questa prova:

• La distribuzione della popolazione è normale e
• I campioni vengono estratti in modo casuale e indipendente.

ANOVA

1. Chiamato anche come Analisi delle variazioni, è un test parametrico di verifica di ipotesi.

2. È un'estensione del test T e del test Z..

3. Viene utilizzato per testare la significatività delle differenze nei valori medi tra più di due gruppi di campioni..

4. Utilizzare il test F per verificare statisticamente l'uguaglianza delle medie e la varianza relativa tra di esse.

5. Presupposti di questa prova:

• La distribuzione della popolazione è normale e
• I campioni sono casuali e indipendenti..
• Omogeneità della varianza campionaria.

6. ANOVA a una via e ANOVA a due vie sono tipi.

7. Statistica F = varianza tra le medie campionarie / varianza all'interno del campione

Test del chi quadrato

1. È un test non parametrico di verifica delle ipotesi..

2. Come test non parametrico, chi quadrato può essere utilizzato:

• prova di bontà.
• come test di indipendenza di due variabili.

3. Aiuta a valutare la bontà di adattamento tra un insieme di osservati e teoricamente attesi.

4. Effettua un confronto tra le frequenze attese e le frequenze osservate.

5. Maggiore è la differenza, maggiore è il valore del chi quadrato.

6. Se non c'è differenza tra le frequenze previste e osservate, quindi il valore del chi quadrato è uguale a zero.

7. Conosciuto anche come il “Bontà di fit test” che determina se una particolare distribuzione si adatta o meno ai dati osservati.

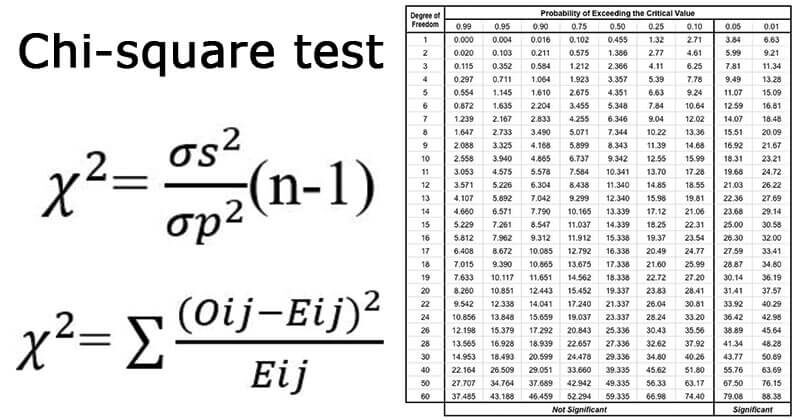
8. È calcolato come:

9. Il chi quadrato viene utilizzato anche per verificare l'indipendenza di due variabili..

10. Condizioni per il test del chi quadrato:

• Raccogli e registra osservazioni casuali.
• nel campione, tutte le entità devono essere indipendenti.
• Nessuno dei gruppi dovrebbe contenere troppo pochi elementi, diciamo meno di 10.
• Il numero totale di articoli ragionevolmente elevato. Normalmente, dovrebbe essere almeno 50, non importa quanto piccolo sia il numero dei gruppi.

11. Il chi quadrato come test parametrico viene utilizzato come test per la varianza della popolazione in base alla varianza del campione.

12. Se prendiamo ciascuno da una raccolta di varianze campionarie, Li dividiamo per la varianza della popolazione nota e moltiplichiamo questi rapporti per (n-1), dove n indica il numero di elementi nel campione, otteniamo i valori del chi quadrato.

13. È calcolato come:

Test U di Mann-Whitney

1. È un test non parametrico di verifica delle ipotesi..

2. Questo test viene utilizzato per indagare se due campioni indipendenti sono stati selezionati da una popolazione con la stessa distribuzione..

3. È una vera controparte non parametrica del test t e fornisce le stime di significatività più accurate., soprattutto quando le dimensioni del campione sono piccole e la popolazione non è normalmente distribuita.

4. Si basa sul confronto di ciascuna osservazione del primo campione con ciascuna osservazione dell'altro campione..

5. La statistica del test utilizzata qui è “tu”.

6. Il valore massimo di “tu” è 'n₁*Nord₂'e il valore minimo è zero.

7. È anche conosciuto come:

• Test di Mann-Whitney Wilcoxon.
• Test di grado Mann-Whitney Wilcoxon.

8. Matematicamente, U è data da:

tu₁ = R₁ – n₁(Nord₁+1) / 2

dove₁ è la dimensione del campione per il campione 1, e R₁ è la somma dei ranghi nel campione 1.

tu₂ = R₂ – n₂(Nord₂+1) / 2

Osservando le tabelle di significato, valori minori di U₁ e tu₂ sono usati. La somma di due valori è data da,

tu₁ + tu₂ = {R₁ – n₁(Nord₁+1) / 2} + {R₂ – n₂(Nord₂+1) / 2}

Sapendo che R₁+ R₂ = N (n + 1) / 2 e N = n₁+ n₂, e fare un po' di algebra, troviamo che la somma è:

tu₁ + tu₂ = n₁*Nord₂

Test di Kruskal-Wallis H

1. È un test non parametrico di verifica delle ipotesi..

2. Questo test viene utilizzato per confrontare due o più campioni indipendenti di dimensioni del campione uguali o diverse..

3. Estende il test U di Mann-Whitney, che viene utilizzato per confrontare solo due gruppi.

4. L'ANOVA unidirezionale è l'equivalente parametrico di questo test.. Ed è per questo che è anche conosciuto come ‘ANOVA unidirezionale nelle gamme.

5. Usa gli intervalli invece dei dati effettivi.

6. Non presuppone che la popolazione sia normalmente distribuita..

7. La statistica del test utilizzata qui è “h”.

Questo completa la discussione di oggi!!

Note finali

Grazie per aver letto!

Spero che l'articolo ti sia piaciuto e che hai aumentato le tue conoscenze sui test statistici per il test di ipotesi nelle statistiche..

Per favore sentiti libero di contattarmi su E-mail

Tutto ciò che non è stato menzionato o vuoi condividere i tuoi pensieri? Sentiti libero di commentare qui sotto e ti ricontatterò.

Per gli articoli rimanenti, Chiedi a Collegamento.

Circa l'autore

Aashi Goyal

Attualmente, Sto perseguendo il mio Bachelor of Technology (B.Tech) in Ingegneria Elettronica e delle Comunicazioni da Universidad Guru Jambheshwar (GJU), Hisar. Sono molto entusiasta delle statistiche, apprendimento automatico e apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute....

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato