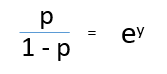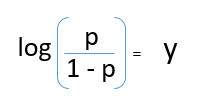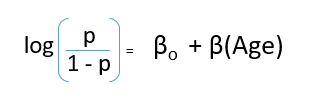Regressione logistica R | Introduzione alla regressione logistica

Panoramica

• Ottieni un'introduzione alla regressione logistica usando R e Python
• La regressione logistica è un popolare algoritmo di classificazione utilizzato per prevedere un risultato binario
• Esistono diverse metriche per valutare un modello di regressione logistica, come matrice di confusione, curva AUC-ROC, eccetera.

introduzione

Ogni algoritmo di apprendimento automatico funziona meglio in un dato insieme di condizioni. Assicurati che il tuo algoritmo soddisfi le ipotesi / requisiti garantisce prestazioni superiori. Nessun algoritmo può essere utilizzato in nessuna condizione. Ad esempio: Hai mai provato ad usarlo regressione lineare in un variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... Dipendente categorico? Non provarci nemmeno! Perché non sarai apprezzato per aver ottenuto valori estremamente bassi della statistica R² e F regolata.

Anziché, in tali situazioni, dovresti provare a usare algoritmi come Logistic Regression, Alberi decisionali, SVM, foresta casuale, eccetera. Per una rapida panoramica di questi algoritmi, Consiglierò la lettura: Concetti di base degli algoritmi di machine learning.

con questo post, ti fornisco conoscenze utili sulla regressione logistica in R. Una volta che hai imparato la regressione lineare, questo è il naturale passo successivo del tuo viaggio. È anche facile da imparare e implementare, ma dovresti conoscere la scienza dietro questo algoritmo.

Ho cercato di spiegare questi concetti nel modo più semplice possibile. Cominciamo.

Cos'è la regressione logistica?

Una è la regressione logistica algoritmo di classificazione. Viene utilizzato per prevedere un risultato binario (1/0, sì / No, Vero / Impostore) dato un insieme di variabili indipendenti. Per rappresentare un risultato binario / categorico, usiamo variabili fittizie. Puoi anche pensare alla regressione logistica come a un caso speciale di regressione lineare quando la variabile di risultato è categoriale, dove usiamo il log delle quote come variabile dipendente. In parole semplici, prevedere la probabilità che si verifichi un evento adattando i dati a una funzione logit.

Derivazione dell'equazione di regressione logistica

La regressione logistica fa parte di una classe più ampia di algoritmi nota come modello lineare generalizzato. (glm). Sopra 1972, Nelder e Wedderburn hanno proposto questo modello nel tentativo di fornire un mezzo per utilizzare la regressione lineare per problemi che non erano direttamente adatti all'applicazione della regressione lineare.. Infatti, proposto una classe di diversi modelli (regressione lineare, ANOVA, regressione di poisson, eccetera.) che includeva la regressione logistica come caso speciale.

L'equazione fondamentale del modello lineare generalizzato è:

G(E(e)) = α + βx1 + γx2

Qui, G () è la funzione di collegamento, E (e) è l'aspettativa della variabile target e α + βx1 + γx2 è il predittore lineare (un, B, γ per prevedere). Il ruolo della funzione di collegamento è “collegamento” l'aspettativa di y al predittore lineare.

Punti importanti

1. GLM non presuppone una relazione lineare tra variabili dipendenti e indipendenti. tuttavia, presuppone una relazione lineare tra la funzione di collegamento e le variabili indipendenti nel modello logit.
2. La variabile dipendente non ha bisogno di essere distribuita normalmente..
3. Non utilizza OLS (Ordinario minimo quadrato) per la stima di parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto..... Anziché, utilizza la stima di massima verosimiglianza (MLE).
4. Gli errori devono essere indipendenti ma non normalmente distribuiti..

Capiamo di più con un esempio:

Ci viene fornito un campione di 1000 clienti. Dobbiamo prevedere la probabilità che un cliente acquisterà (e) una determinata rivista o meno. Come potete vedere, abbiamo una variabile di risultato categoriale, useremo la regressione logistica.

Per iniziare con la regressione logistica, Per prima cosa scriverò la semplice equazione di regressione lineare con la variabile dipendente racchiusa in una funzione di collegamento:

                           G(e) = βo + B(Età)         ---- (un)

Nota: Per facilitare la comprensione, Ho considerato 'Età’ come variabile indipendente.

Nella regressione logistica, ci occupiamo solo della probabilità della variabile dipendente del risultato (successo o fallimento). Come descritto sopra, G () è la funzione di collegamento. Questa funzione è impostata da due cose: probabilità di successo (P) e probabilità di fallimento (1-P). p deve soddisfare i seguenti criteri:

1. dovrebbe essere sempre positivo (da pag> = 0)
2. Deve essere sempre minore di uguale a 1 (da pag <= 1)

Ora, li soddisferemo semplicemente 2 condizioni e arriveremo al nocciolo della regressione logistica. Per impostare la funzione di collegamento, indicheremo g () con ‘p’ inizialmente e alla fine finiremo per derivare questa funzione.

Poiché la probabilità deve essere sempre positiva, metteremo l'equazione lineare in forma esponenziale. Per qualsiasi valore di pendenza e variabile dipendente, l'esponente di questa equazione non sarà mai negativo.

p = esp(βo + B(Età)) = e^(βo + B(Età))    ------- (B)

Affinché la probabilità sia inferiore a 1, dobbiamo dividere p per un numero maggiore di p. Questo può essere fatto semplicemente:

p = esp(βo + B(Età)) / esp(βo + B(Età)) + 1   = e^(βo + B(Età)) / e^(βo + B(Età)) + 1    ----- (C)

Usando (un), (B) e (C), possiamo ridefinire la probabilità come:

              p = e^y/ 1 + e^y           --- (D)

dove p è la probabilità di successo. Questo (D) è la funzione logit

Se p è la probabilità di successo, 1-p sarà la probabilità di fallimento che può essere scritta come:

q = 1 - p = 1 - (e^y/ 1 + e^y)    --- (e)

dove qual è la probabilità di fallimento

quando si divide, (D) / (e), otteniamo,

Dopo aver preso il registro su entrambi i lati, otteniamo,

tronco d'albero (P / 1-P) è la funzione di collegamento. La trasformazione logaritmica della variabile di risultato consente di modellare un'associazione non lineare in modo lineare.

Dopo aver sostituito il valore di y, otterremo:

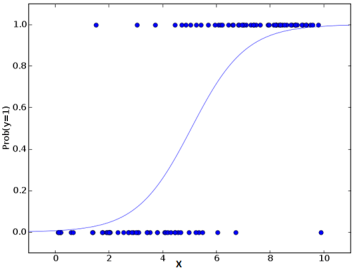
Questa è l'equazione utilizzata nella regressione logistica. Qui (P / 1-P) è il rapporto dispari. Quando si determina che il logaritmo del rapporto dispari è positivo, la probabilità di successo è sempre maggiore di 50%. Di seguito è riportato un tipico diagramma del modello logistico. Puoi vedere che la probabilità non scende mai al di sotto 0 e al di sopra 1.

Prestazioni del modello di regressione logistica

Per valutare le prestazioni di un modello di regressione logistica, dobbiamo considerare alcune metriche. Indipendentemente dallo strumento (SAS, R, Pitone) in cui lavorerei, cerca sempre:

1. AIC (Akaike criteri di informazione) – L'analoga metrica di R2 aggiustata nella regressione logistica è AIC. AIC è la misura di adattamento che penalizza il modello per il numero di coefficienti nel modello. Perciò, preferiamo sempre il modello con un valore AIC minimo.

2. Deviazione nulla e deviazione residua – La devianza nulla indica la risposta prevista da un modello con nient'altro che un'intercettazione. Abbassa il valore, meglio il modello. La devianza residua indica la risposta prevista da un modello quando si sommano variabili indipendenti. Abbassa il valore, meglio il modello.

3. Matrice di confusione: Non è altro che una rappresentazione tabellare dei valori effettivi rispetto a quelli previsti. Questo ci aiuta a trovare l'accuratezza del modello ed evitare il sovradattamento.. Ecco come appare:

Fonte: (tappo – n – punto)

Puoi calcolare il precisione del tuo modello con:

Dalla matrice di confusione, la specificità e la sensibilità possono essere derivate come illustrato di seguito:

Specificità e sensibilità giocano un ruolo cruciale nella derivazione della curva ROC..

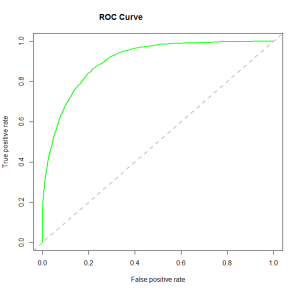
4. curva ROC: La caratteristica di funzionamento del ricevitore (ROC) riassume le prestazioni del modello valutando i compromessi tra il tasso positivo reale (sensibilità) e il tasso di falsi positivi (1 specificità). Per tracciare ROC, è opportuno assumere p> 0.5 poiché siamo più interessati alla percentuale di successo. ROC riassume il potere predittivo per tutti i possibili valori di p> 0.5. L'area sotto la curva (AUC), Chiamai indiceIl "Indice" È uno strumento fondamentale nei libri e nei documenti, che consente di individuare rapidamente le informazioni desiderate. In genere, Viene presentato all'inizio di un'opera e organizza i contenuti in modo gerarchico, compresi capitoli e sezioni. La sua corretta preparazione facilita la navigazione e migliora la comprensione del materiale, rendendolo una risorsa essenziale sia per gli studenti che per i professionisti in vari settori.... precisione (UN) o indice di concordanza, è una metrica di prestazione perfetta per la curva ROC. Maggiore è l'area sotto la curva, migliore è il potere predittivo del modello. Di seguito è riportata una curva ROC di esempio. Il ROC di un modello predittivo perfetto ha TP uguale a 1 e FP pari a 0. Questa curva toccherà l'angolo superiore sinistro del grafico.

Nota: Per le prestazioni del modello, puoi anche considerare la funzione di probabilità. Si chiama così perché seleziona i valori dei coefficienti che massimizzano la probabilità di spiegare i dati osservati.. Indica la bontà di adattamento quando il suo valore è vicino a uno e uno scarso adattamento dei dati quando il suo valore è vicino a zero..

Modello di regressione logistica in R e Python

Il codice R è riportato di seguito, ma se sei un utente Python, Ecco un'incredibile finestra di codice per creare il tuo modello di regressione logistica. Non c'è bisogno di aprire Jupyter, puoi fare tutto qui:

Tenendo conto della disponibilità, Ho costruito questo modello sul nostro problema di pratica: il set di dati Dressify. Puoi scaricarlo qui.

Senza approfondire l'ingegneria delle funzionalità, Ecco il semplice script del modello di regressione logistica:

set(«C:/Utenti/manish/Desktop/dressdata')

#load data
train <- leggi.csv('Train_Old.csv')

#create training and validation data from given data
install.packages('caTools')
biblioteca(caTools)

set.seme(88)
diviso <- sample.split(treno$Consigliato, Rapporto di divisione = 0.75)

#get training and test data
dresstrain <- sottoinsieme(treno, split == VERO)
dresstest <- sottoinsieme(treno, split == FALSO)

#logistic regression model
model <- glm (Consigliato ~ .-ID, dati = dresstrain, famiglia = binomio)
riepilogo(modello)

prevedere <- prevedere(modello, tipo="risposta")

#confusion matrix
table(dresstrain$Consigliato, prevedere > 0.5)

#ROCR Curve
library(ROCR ·)
ROCRpred <- predizione(prevedere, dresstrain$Consigliato)
ROCRperf <- performance art(ROCRpred, 'tpr','fpr')
complotto(ROCRperf, colorizzare = VERO, text.adj = c(-0.2,1.7))

#plot glm
library(ggplot2)
ggplot(dresstrain, aes(x=Valutazione, y=Consigliato)) + geom_point() + 
stat_smooth(metodo="glm", famiglia="binomiale", se=FALSO)

Questi dati richiedono molta pulizia e ingegneria delle funzionalità. Lo scopo di questo articolo mi ha impedito di mantenere l'esempio focalizzato sulla costruzione del modello di regressione logistica.. Questi dati sono a disposizione per esercitarsi. Ti consiglio di lavorare su questo problema. C'è molto da imparare.

Note finali

In questa fase, conoscerai già la scienza alla base della regressione logistica. Ho visto molte volte che le persone conoscono l'uso di questo algoritmo senza avere conoscenza dei suoi concetti fondamentali.. Ho fatto del mio meglio per spiegare questa parte nel modo più semplice possibile.. L'esempio sopra mostra solo lo scheletro dell'uso della regressione logistica in R. Prima di avvicinarsi davvero a questa fase, dovresti dedicare il tuo tempo cruciale all'ingegneria delle funzionalità.

Cosa c'è di più, Ti consiglio di lavorare su questo insieme di problemi. Esploreresti cose che potresti non aver mai affrontato prima.

Mi sono perso qualcosa di importante? Trovi utile questo articolo? Condividi le tue opinioni / pensieri nella sezione commenti qui sotto.

Se ti piace quello che hai appena letto e vuoi continuare a imparare l'analisi, iscriviti alle nostre email, Seguici su Twitter o come il nostro pagina Facebook.

Imparentato