Iniziamo con una breve esposizione del problema.
Dichiarazione problema: creare un semplice modello di regressione lineare per prevedere l'aumento di stipendio utilizzando anni di esperienza.
Inizia importando le librerie necessarie
le librerie richieste sono panda, NumPy per lavorare con frame di dati, matplotlib, seaborn per visualizzazioni e sklearn, statmodels per costruire modelli di regressione.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from scipy import stats
from scipy.stats import probplot
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn import preprocessing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_scoreUna volta terminata l'importazione delle librerie, creiamo un frame di dati panda dal file CSV
df = pd.read_csv(“Salary_Data.csv”)
Esegui EDA (analisi esplorativa dei dati)
I passaggi fondamentali di EDA sono:
- Identificare il numero di funzioni o colonne
- Identificare le caratteristiche o colonne
- Identificare la dimensione del set di dati
- Identificazione dei tipi di dati delle caratteristiche
- Verificare se il set di dati ha celle vuote
- Identificare il numero di celle vuote per caratteristiche o colonne
- Gestione di valori mancanti e valori anomali
- Codifica di variabili categoriali
- Analisi grafica univariata, bivariato
- NormalizzazioneLa standardizzazione è un processo fondamentale in diverse discipline, che mira a stabilire norme e criteri uniformi per migliorare la qualità e l'efficienza. In contesti come l'ingegneria, Istruzione e amministrazione, La standardizzazione facilita il confronto, Interoperabilità e comprensione reciproca. Nell'attuazione degli standard, si promuove la coesione e si ottimizzano le risorse, che contribuisce allo sviluppo sostenibile e al miglioramento continuo dei processi.... y escalado
len(df.colonne) # identificare il numero di funzionidf.colonne # identificare le caratteristiche
df.shape # identify the size of of the datasetUn "dataset" o conjunto de datos es una colección estructurada de información, que puede ser utilizada para análisis estadísticos, machine learning o investigación. Los datasets pueden incluir variables numéricas, categóricas o textuales, y su calidad es crucial para obtener resultados fiables. Su uso se extiende a diversas disciplinas, como la medicina, la economía y la ciencia social, facilitando la toma de decisiones informadas y el desarrollo de modelos predictivos....df.dtypes # identify the datatypes of the featuresdf.isnull().values.any() # checking if dataset has empty cellsdf.isnull().sum() # identify the number of empty cellsIl nostro set di dati ha due colonne: Anni di esperienza, Stipendio. Ed entrambi sono di tipo float. Ho 30 record e non abbiamo valori nulli o valori anomali nel nostro set di dati.
Analisi grafica univariata
Per analisi univariate, avere Istogramma, grafico della densità, trama a scatola oh violino, e Grafico QQ normale. Ci aiutano a capire la distribuzione dei punti dati e la presenza di outlier.
un diagramma di violinoEl diagrama de violín es una representación gráfica que combina características de un boxplot y un gráfico de densidad. Se utiliza para visualizar la distribución de un conjunto de datos, mostrando tanto la mediana como la variabilidad a través de su forma, que se asemeja a un violín. Este tipo de gráfico es muy útil en análisis estadísticos, ya que permite comparar múltiples distribuciones de forma clara y efectiva.... es un método para trazar datos numéricos. È simile a un box plot, con l'aggiunta di un diagramma di densità dei grani ruotato su ciascun lato.
Codice Python:
# Histogram
# We can use either plt.hist or sns.histplot
plt.figure(figsize=(20,10))
plt.subplot(2,4,1)
plt.hist(df['YearsExperience'], density=False)
plt.title("Histogram of 'YearsExperience'")
plt.subplot(2,4,5)
plt.hist(df['Salary'], density=False)
plt.title("Histogram of 'Salary'")
# Density plot
plt.subplot(2,4,2)
sns.distplot(df['YearsExperience'], kde=True)
plt.title("Density distribution of 'YearsExperience'")
plt.subplot(2,4,6)
sns.distplot(df['Salary'], kde=True)
plt.title("Density distribution of 'Salary'")
# boxplot or violin plot
# A violin plot is a method of plotting numeric data. It is similar to a box plot,
# with the addition of a rotated kernel density plot on each side
plt.subplot(2,4,3)
# plt.boxplot(df['YearsExperience'])
sns.violinplot(df['YearsExperience'])
# plt.title("Boxlpot of 'YearsExperience'")
plt.title("Violin plot of 'YearsExperience'")
plt.subplot(2,4,7)
# plt.boxplot(df['Salary'])
sns.violinplot(df['Salary'])
# plt.title("Boxlpot of 'Salary'")
plt.title("Violin plot of 'Salary'")
# Normal Q-Q plot
plt.subplot(2,4,4)
probplot(df['YearsExperience'], plot=plt)
plt.title("Q-Q plot of 'YearsExperience'")
plt.subplot(2,4,8)
probplot(df['Salary'], plot=plt)
plt.title("Q-Q plot of 'Salary'")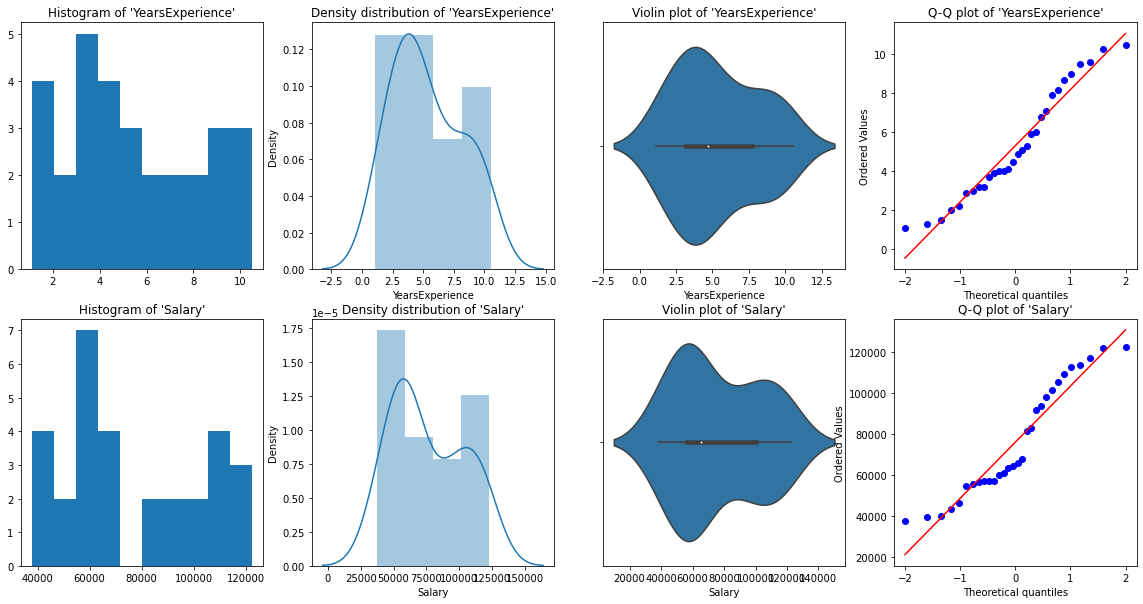
Dalle rappresentazioni grafiche sopra, possiamo dire che non ci sono outlier nei nostri dati, e YearsExperience looks like normally distributed, and Salary doesn't look normal. Possiamo verificarlo usando Shapiro Test.
Codice Python:
# Def a function to run Shapiro test
# Defining our Null, Alternate Hypothesis
Ho = 'Data is Normal'
Ha="Data is not Normal"
# Defining a significance value
alpha = 0.05
def normality_check(df):
for columnName, columnData in df.iteritems():
print("Shapiro test for {columnName}".format(columnName=columnName))
res = stats.shapiro(columnData)
# print(res)
pValue = round(res[1], 2)
# Writing condition
if pValue > alpha:
print("pvalue = {pValue} > {alpha}. We fail to reject Null Hypothesis. {Ho}".format(pValue=pValue, alpha=alpha, Ho=Ho))
else:
print("pvalue = {pValue} <= {alpha}. We reject Null Hypothesis. {Ha}".format(pValue=pValue, alpha=alpha, Ha=Ha))
# Drive code
normality_check(df)Il nostro istinto grafico era corretto. Anni L'esperienza è distribuita normalmente e lo stipendio non è distribuito normalmente.
Visualizzazione bivariata
per dati numerici vs dati numerici, possiamo disegnare i seguenti grafici
- Grafico a dispersione
- Grafico a linee
- Mappa di calore per correlazione
- Trama comune
Codice Python per più pacchi:
# Scatterplot & Line plots
plt.figure(figsize=(20,10))
plt.subplot(1,3,1)
sns.scatterplot(data=df, x="YearsExperience", y="Salary", hue="YearsExperience", alpha=0.6)
plt.title("Scatter plot")
plt.subplot(1,3,2)
sns.lineplot(data=df, x="YearsExperience", y="Salary")
plt.title("Line plot of YearsExperience, Salary")
plt.subplot(1,3,3)
sns.lineplot(data=df)
plt.title('Line Plot')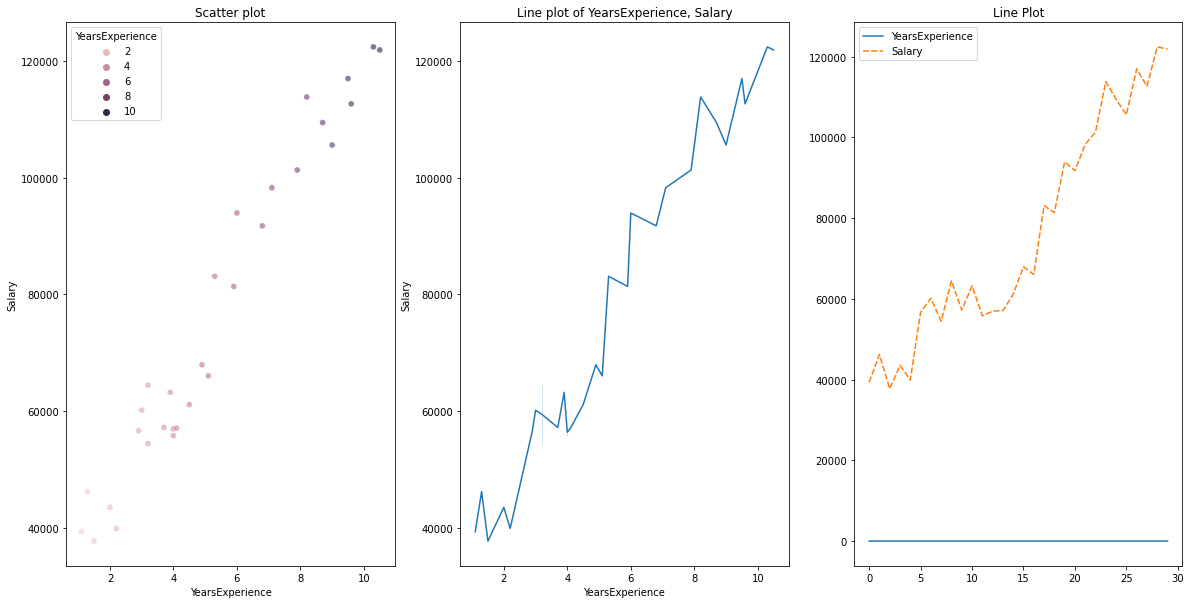
# heatmap
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
sns.heatmap(data=df, cmap="YlGnBu", annot = True)
plt.title("Heatmap using seaborn")
plt.subplot(1, 2, 2)
plt.imshow(df, cmap ="YlGnBu")
plt.title("Heatmap using matplotlib")
# Joint plot
sns.jointplot(x = "YearsExperience", y = "Salary", kind = "reg", data = df)
plt.title("Joint plot using sns")
# kind can be hex, kde, scatter, reg, hist. When kind='reg' it shows the best fit line.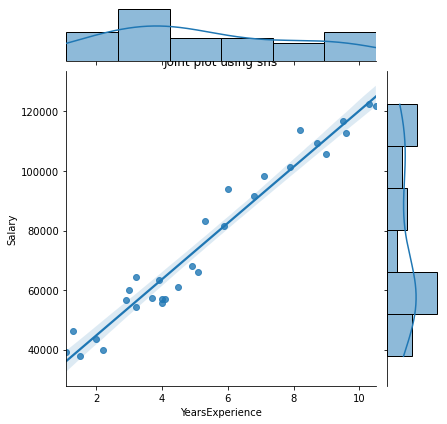
Controlla se c'è qualche correlazione tra le variabili usando df.corr ()
print("Correlation: "+ 'n', df.corr()) # 0.978 which is high positive correlation
# Draw a heatmap for correlation matrix
plt.subplot(1,1,1)
sns.heatmap(df.corr(), annot=True)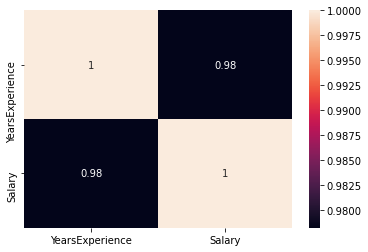
correlazione = 0,98, che è una correlazione altamente positiva. Esto significa que la variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... dependiente aumenta a misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... que aumenta la variable independiente.
Normalizzazione
Come possiamo vedere, c'è una grande differenza tra i valori delle colonne YearsExperience, Stipendio. Possiamo usare Normalization per modificare i valori delle colonne numeriche nel set di dati per utilizzare una scala comune, senza distorcere le differenze negli intervalli di valori o perdere informazioni.
Noi usiamo sklearn.preprocessing.Normalize per normalizzare i nostri dati. Restituisce i valori tra 0 e 1.
# Create new columns for the normalized values
df['Norm_YearsExp'] = preprocessing.normalize(df[['YearsExperience']], axis=0)
df['Norm_Salary'] = preprocessing.normalize(df[['Salary']], axis=0)
df.head()Regressione lineare usando scikit-learn
LinearRegression(): LinearRegression è conforme a un modello lineare con coefficienti β = (1,…, p) minimizzare la somma dei quadrati residua tra gli obiettivi osservati nel set di dati e gli obiettivi previsti dall'approssimazione lineare.
def regression(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x,y)
# Instantiating the LinearRegression object
regressor = LinearRegression()
# Training the model
regressor.fit(x,y)
# Checking the coefficients for the prediction of each of the predictor
print('n'+"Coeff of the predictor: ",regressor.coef_)
# Checking the intercept
print("Intercept: ",regressor.intercept_)
# Predicting the output
y_pred = regressor.predict(x)
# print(y_pred)
# Checking the MSE
print("Mean squared error(MSE): %.2f" % mean_squared_error(y, y_pred))
# Checking the R2 value
print("Coefficient of determination: %.3f" % r2_score(y, y_pred)) # Evaluates the performance of the model # says much percentage of data points are falling on the best fit line
# visualizing the results.
plt.figure(figsize=(18, 10))
# Scatter plot of input and output values
plt.scatter(x, y, color="teal")
# plot of the input and predicted output values
plt.plot(x, regressor.predict(x), color="Red", linewidth=2 )
plt.title('Simple Linear Regression')
plt.xlabel('YearExperience')
plt.ylabel('Salary')
# Driver code
regression(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
regression(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyRaggiungiamo una precisione di 95,7% con scikit-impara, pero no hay mucho margenEl margen es un término utilizado en diversos contextos, como la contabilidad, la economía y la impresión. En contabilidad, se refiere a la diferencia entre los ingresos y los costos, lo que permite evaluar la rentabilidad de un negocio. En el ámbito editorial, el margen es el espacio en blanco alrededor del texto en una página, que facilita la lectura y proporciona una presentación estética. Su correcta gestión es esencial... para comprender la información detallada sobre la relevancia de las características de este modelo. Quindi costruiamo un modello usando statsmodels.api, statsmodels.formula.api
Regressione lineare utilizzando statsmodel.formula.api (smf)
I predittori in statsmodels.formula.api devono essere elencati singolarmente. E in questo metodo, una costante viene aggiunta automaticamente ai dati.
def smf_ols(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x)
# train the model
model = smf.ols('y~x', data=df).fit()
# print model summary
print(model.summary())
# Predict y
y_pred = model.predict(x)
# print(type(y), type(y_pred))
# print(y, y_pred)
y_lst = y.Salary.values.tolist()
# y_lst = y.iloc[:, -1:].values.tolist()
y_pred_lst = y_pred.tolist()
# print(y_lst)
data = [y_lst, y_pred_lst]
# print(data)
res = pd.DataFrame({'Actuals':data[0], 'Predicted':data[1]})
# print(res)
plt.scatter(x=res['Actuals'], y=res['Predicted'])
plt.ylabel('Predicted')
plt.xlabel('Actuals')
res.plot(kind='bar',figsize=(10,6))
# Driver code
smf_ols(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
# smf_ols(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracy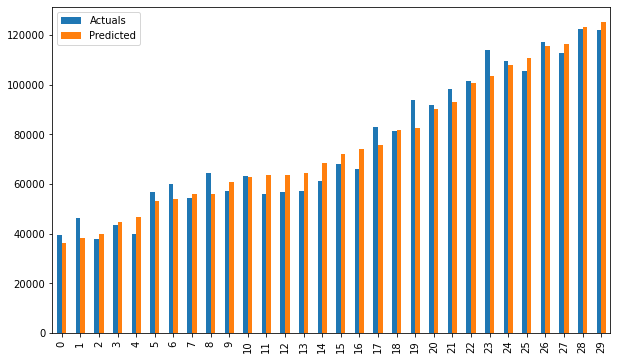
Regressione utilizzando statsmodels.api
Non è più necessario elencare i predittori individualmente.
statsmodels.regression.linear_model.OLS (anche, exog)
endogè la variabile dipendenteexogè la variabile indipendente. Un'intercettazione non è inclusa per impostazione predefinita e deve essere aggiunta dall'utente (usando add_constant).
# Create a helper function
def OLS_model(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# Add a constant term to the predictor
x = sm.add_constant(x)
# print(x)
model = sm.OLS(y, x)
# Train the model
results = model.fit()
# print('n'+"Confidence interval:"+'n', results.conf_int(alpha=0.05, cols=None)) #Returns the confidence interval of the fitted parameters. The default alpha=0.05 returns a 95% confidence interval.
print('n'"Model parameters:"+'n',results.params)
# print the overall summary of the model result
print(results.summary())
# Driver code
OLS_model(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
OLS_model(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyRaggiungiamo una precisione di 95,7%, che è abbastanza buono
¿Qué dice la tabla de resumenIl "tabla de resumen" es una herramienta eficaz que condensa información clave de un tema específico en un formato visual y accesible. Utilizada en diversos campos, como la educación y la investigación, facilita la comprensión y el análisis de datos. Su estructura permite a los usuarios identificar rápidamente los puntos esenciales, promoviendo una mejor retención del conocimiento y una comparación más sencilla entre diferentes conceptos o variables.... del modello? ?
È sempre importante comprendere alcuni termini nella tabella riassuntiva del modello di regressione in modo da poter conoscere le prestazioni del nostro modello e la rilevanza delle variabili di input.
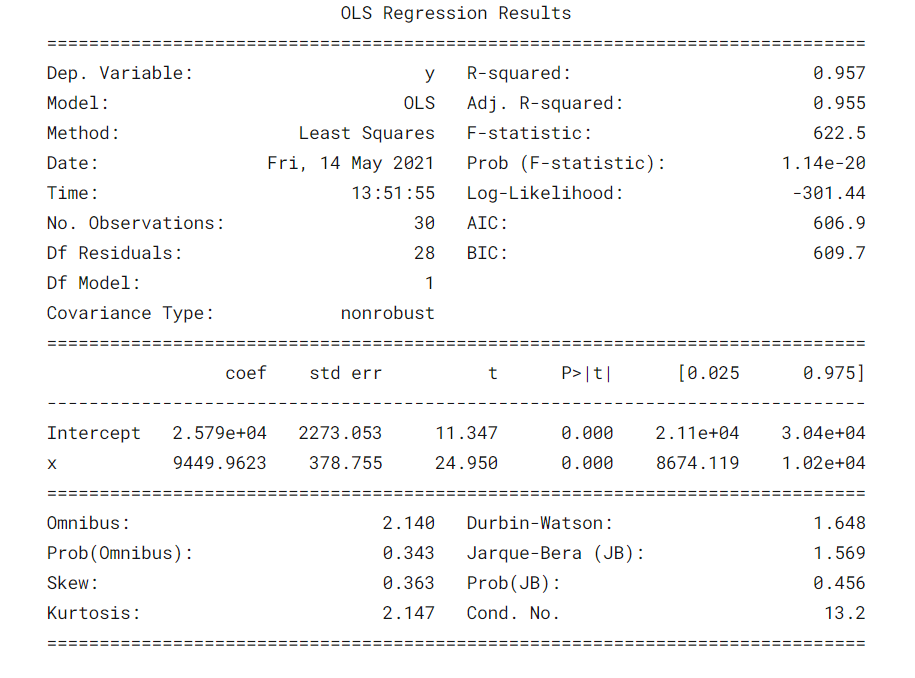
Alcuni parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... importantes que deben tenerse en cuenta son el valor de R cuadrado, Adj. Valore R al quadrato, Statistica F, probabilmente (Statistica F), coefficiente di intercettazione e variabili di input, P> | T |.
- R-quadrato è il coefficiente di determinazione. Una misura statistica che dice che gran parte dei punti dati sono sulla linea di miglior adattamento. Un valore di R al quadrato più vicino a 1 per un modello che si adatti bene.
- Adj. R-squared penalizza il valore di R-squared se continuiamo ad aggiungere le nuove funzionalità che non contribuiscono alla previsione del modello. Si Adj. R quadrato valore <Valore R al quadrato, è un segno che abbiamo predittori irrilevanti nel modello.
- La estadística F o prueba F nos ayuda a aceptar o rechazar la ipotesi nullaL'ipotesi nulla è un concetto fondamentale in statistica che stabilisce un'affermazione iniziale su un parametro di popolazione. Il suo scopo è quello di essere testato e, se confutato, ci permette di accettare l'ipotesi alternativa. Questo approccio è essenziale nella ricerca scientifica, in quanto fornisce un quadro di riferimento per valutare le prove empiriche e prendere decisioni basate sui dati. La sua formulazione e analisi sono cruciali negli studi statistici..... Confronta il modello solo intercetta con il nostro modello con caratteristiche. L'ipotesi nulla è “tutti i coefficienti di regressione sono uguali a zero e ciò significa che entrambi i modelli sono uguali”. L'ipotesi alternativa e' intercettare l'unico modello peggiore del nostro modello, il che significa che i nostri coefficienti aggiunti hanno migliorato le prestazioni del modello. Se è probabile (Statistica F) <0.05 e la statistica F è un valore alto, rifiutiamo l'ipotesi nulla. Significa che c'è una buona relazione tra le variabili di input e di output.
- coef visualizza i coefficienti stimati delle corrispondenti caratteristiche di input
- T-test parla della relazione tra l'output e ciascuna delle variabili di input individualmente. L'ipotesi nulla è 'il coefficiente di una caratteristica di input è 0'. L'ipotesi alternativa è "il coefficiente di una caratteristica di input non è 0". Se pvalue 0.05.
Bene, ora sappiamo come trarre importanti inferenze dalla tabella di riepilogo del modello, quindi ora diamo un'occhiata ai parametri del nostro modello e valutiamo il nostro modello.
Nel nostro caso, il valore di R al quadrato (0,957) è vicino ad Adj. Il valore di R al quadrato (0,955) è un buon segno che le caratteristiche di input stanno contribuendo al modello predittore.
La statistica F è un numero alto e p (Statistica F) è quasi 0, il che significa che il nostro modello è migliore del modello a intersezione singola.
Il valore p del t-test per la variabile di input è inferiore a 0.05, quindi c'è una buona relazione tra la variabile di input e la variabile di output.
Perciò, concludiamo dicendo che il nostro modello sta funzionando bene ✔😊
In questo blog, Abbiamo imparato le basi della regressione lineare semplice (reflex), costruire un modello lineare utilizzando diverse librerie Python e fare inferenze dalla tabella riassuntiva dei modelli statistici OLS.
Riferimenti:
Interpretazione della tabella riassuntiva dal modello statistico OLS
Visualizzazioni: Istogramma, Grafico della densità, trama del violino, trama a scatola, Grafico QQ normale, Grafico a dispersione, grafico a linee, mappa di calore, trama comune
Guarda il taccuino completo di my GitHub deposito.
Spero che questo sia un blog informativo per principianti. Per favore, Si prega di votare se lo trovi utile I tuoi commenti sono molto apprezzati. Buon apprendimento !! ?
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.
