
introduzione:
Uno dei passaggi più importanti nell'ambito della preelaborazione dei dati è il rilevamento e la gestione dei valori anomali, in quanto possono influire negativamente sull'analisi statistica e sul processo di addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.... di un algoritmo di machine learning, con conseguente minore precisione.
1. Cosa sono gli outlier?? ?
Abbiamo tutti sentito parlare dell'idioma "strano", che significa qualcosa di insolito rispetto agli altri in un gruppo.
Allo stesso modo, un outlier è un'osservazione in un dato set di dati che è lontana dal resto delle osservazioni. Ciò significa che un valore anomalo è molto più grande o più piccolo dei valori rimanenti nel set..
2. Perché si verificano??
Un outlier può verificarsi a causa della variabilità dei dati, o a causa di un errore sperimentale / errore umano.
Può indicare un errore sperimentale o una grande asimmetria nei dati (distribuzione di colla pesante).
3. che influiscono?
Nelle statistiche, abbiamo tre misure di tendenza centrale: Media, MedianoLa mediana è una misura statistica che rappresenta il valore centrale di un insieme di dati ordinati. Per calcolarlo, I dati sono organizzati dal più basso al più alto e viene identificato il numero al centro. Se c'è un numero pari di osservazioni, I due valori fondamentali sono mediati. Questo indicatore è particolarmente utile nelle distribuzioni asimmetriche, poiché non è influenzato da valori estremi.... & Moda. Aiutaci a descrivere i dati.
La media è il misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... Accurato per descrivere i dati quando non sono presenti valori anomali.
La mediana viene utilizzata se c'è un valore anomalo nel set di dati.
La modalità viene utilizzata se c'è un valore anomalo E circa la metà o più dei dati è uguale.
Il “media” è l'unica misura della tendenza centrale che è influenzata da valori anomali, che a sua volta influenza la deviazione standard.
Esempio:
Considera un piccolo set di dati, campione = [15, 101, 18, 7, 13, 16, 11, 21, 5, 15, 10, 9]. guardandolo, puoi dire rapidamente che '101’ è un valore anomalo molto più grande degli altri valori.

Dai calcoli di cui sopra, possiamo dire chiaramente che la Media è più colpita della Mediana.
4. Rilevamento di valori atipici
Se il nostro set di dati è piccolo, possiamo rilevare il valore anomalo semplicemente guardando il set di dati. Ma, E se avessimo un grande set di dati?, come identifichiamo gli outlier? Dobbiamo usare tecniche di visualizzazione e matematica.
Di seguito sono riportate alcune delle tecniche per rilevare i valori anomali.
- Diagrammi scatolariDiagrammi a scatola, Conosciuto anche come diagrammi a scatola e baffi, sono strumenti statistici che rappresentano la distribuzione di un dataset. Questi diagrammi mostrano la mediana, quartili e valori anomali, Consentire la visualizzazione della variabilità e della simmetria dei dati. Sono utili nel confronto tra diversi gruppi e nell'analisi esplorativa, Rendendo più facile identificare tendenze e modelli nei dati....
- Punteggio Z
- Intervallo tra quantili (IQR)
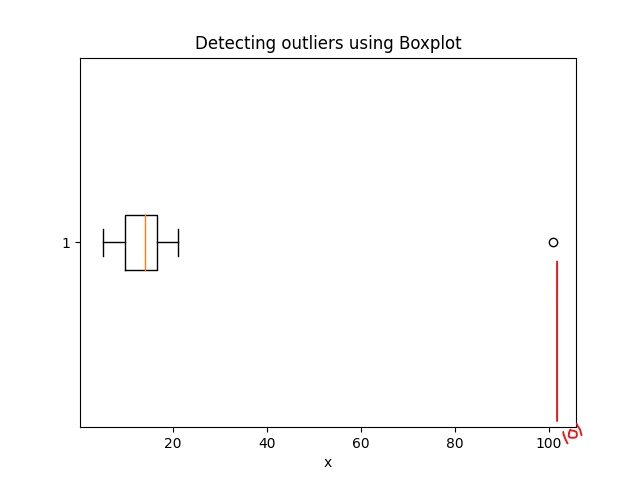
4.1 Rilevamento di anomalie tramite Boxplot:
Il codice Python per il diagramma box è:
import matplotlib.pyplot as plt
plt.boxplot(campione, vert=Falso)
plt.titolo("Rilevamento di valori anomali utilizzando Boxplot")
plt.xlabel('Campione')
4.2 Rilevamento di valori anomali utilizzando i punteggi Z
Criteri: qualsiasi punto dati il cui punteggio Z non rientra nella 3a deviazione standard è un valore anomalo.
Passi:
- passare attraverso tutti i punti dati e calcolare il punteggio Z utilizzando la formula (Xi-media) / standard.
- Impostare un valore soglia di 3 e contrassegnare i punti dati il cui valore Z-score assoluto è maggiore della soglia come valori anomali.
import numpy as np outliers = [] def detect_outliers_zscore(dati): thres = 3 media = np.mean(dati) std = np.std(dati) # Stampa(Significare, standard) per i dati: z_score = (i-mean)/std if (np.abs(z_score) > thres): outliers.append(io) return outliers# Driver code sample_outliers = detect_outliers_zscore(campione) Stampa("Valori anomali del metodo Z-scores: ", sample_outliers)
I risultati del codice precedente: Valori anomali del metodo Z-score: [101]
4.3 Rilevamento di valori anomali utilizzando l'intervallo tra quantili (IQR)
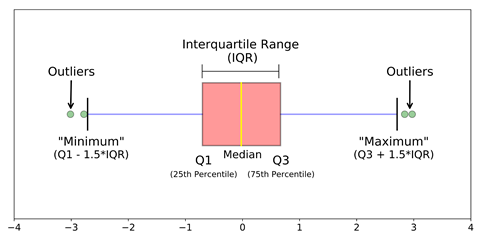
Criteri: I punti dati che si trovano 1,5 volte l'IQR sopra Q3 e sotto Q1 sono valori anomali.
Passi:
- Ordinare il set di dati in ordine crescente
- calcolare il primo e il terzo quartile (Q1, Q3)
- calcola IQR = Q3-Q1
- calcola limite inferiore = (Q1–1,5 * IQR), limite superiore = (Q3 + 1.5 * IQR)
- Esaminare i valori nel set di dati e controllare quelli che scendono al di sotto del limite inferiore e superiore e contrassegnarli come valori anomali
Codice Python:
valori anomali = []
def detect_outliers_iqr(dati):
dati = ordinati(dati)
q1 = np.percentile(dati, 25)
q3 = np.percentile(dati, 75)
# Stampa(Q1, Q3 ·)
IQR = q3-q1
lwr_bound = q1-(1.5*IQR)
upr_bound = q3+(1.5*IQR)
# Stampa(lwr_bound, upr_bound)
per i dati:
Se (io<lwr_bound o i>upr_bound):
outliers.append(io)
return outliers# Driver code
sample_outliers = detect_outliers_iqr(campione)
Stampa("Valori anomali del metodo IQR: ", sample_outliers)
I risultati del codice precedente: Valori anomali del metodo IQR: [101]
5. Gestione degli outlier
Finora abbiamo appreso del rilevamento dei valori anomali. La domanda principale è COSA facciamo con i valori anomali??
Ecco alcuni dei metodi per gestire gli outlier.
- Ordinare / rimuovi valori anomali
- Rivestimenti e pavimentazioni a base quantile
- imputazione media / mediano
5.1 Ritagliare / Rimozione dei valori anomali
In questa tecnica, rimuoviamo gli outlier dal set di dati. Anche se non è una buona pratica da seguire.
Codice Python per rimuovere l'outlier e copiare il resto degli elementi in un'altra matrice.
# Trimming
for i in sample_outliers:
a = np.delete(campione, np.dove(campione==i))
Stampa(un)
# Stampa(len(campione), len(un))
Outlier '101’ viene eliminato e il resto dei punti dati viene copiato in un'altra matrice 'a'.
5.2 Rivestimenti e pavimenti a base di quantili
In questa tecnica, Il valore anomalo è limitato a un determinato valore superiore al valore percentile 90 o è ridotto a un fattore inferiore al valore percentile 10.
Codice Python:
# Informatica 10, 90th percentiles and replacing the outliers
tenth_percentile = np.percentile(campione, 10)
ninetieth_percentile = np.percentile(campione, 90)
# Stampa(tenth_percentile, ninetieth_percentile)b = np.where(campione<tenth_percentile, tenth_percentile, campione)
b = np.where(B>ninetieth_percentile, ninetieth_percentile, B)
# Stampa("Campione:", campione)
Stampa("Nuovo array:",B)
I risultati del codice precedente: Nuova matrice: [15, 20.7, 18, 7.2, 13, 16, 11, 20.7, 7.2, 15, 10, 9]
Punti dati più piccoli del percentile 10 vengono sostituiti con il valore percentile 10 e punti dati più grandi del percentile 90 vengono sostituiti con il valore percentile 90.
5.3 imputazione media / mediano
Poiché il valore medio è fortemente influenzato dai valori anomali, Si consiglia di sostituire i valori anomali con il valore mediano.
Codice Python:
mediana = np.mediana(campione)# Replace with median
for i in sample_outliers:
c = np.where(campione==i, 14, campione)
Stampa("Campione: ", campione)
Stampa("Nuovo array: ",C)
# Stampa(x.dtype)
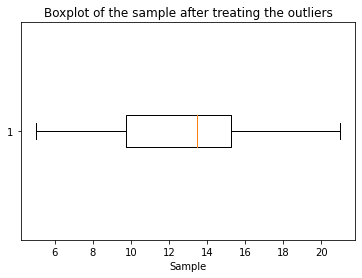
Visualizzazione dei dati dopo aver eseguito l'outlier
plt.boxplot(C, vert=Falso)
plt.titolo("Boxplot del campione dopo aver trattato i valori anomali")
plt.xlabel("Campione")
Riepilogo:
In questo blog, abbiamo appreso di un'importante fase di pre-elaborazione dei dati che è l'elaborazione anomala. Ora conosciamo diversi metodi per rilevare e trattare i valori anomali.
Riferimenti:
Z-score per il rilevamento di valori anomali
IQR per il rilevamento di anomalie
Repository GitHub per consultare il notebook Jupyter
Spero che questo blog ti aiuti a capire il concetto di outlier. Per favore, vota se ti piace. Buon apprendimento !! ?
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.






