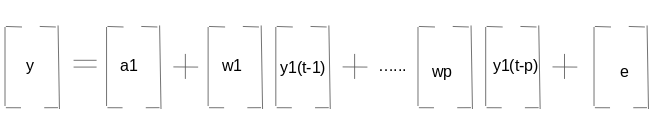Serie temporali multivariate | Regressione automatica vettoriale (DOVE)

introduzione

Il tempo è il fattore più critico nel decidere se un'azienda aumenterà o diminuirà. Questo è il motivo per cui vediamo le vendite nei negozi e nelle piattaforme di e-commerce in linea con i festival.. Queste aziende analizzano anni di dati di spesa per capire il momento migliore per aprire le porte e vedere un aumento della spesa dei consumatori..

Ma, Come puoi?, come scienziato dei dati, eseguire questa analisi? Non preoccuparti, non hai bisogno di costruire una macchina del tempo! La modellazione delle serie temporali è una tecnica potente che funge da gateway per comprendere e prevedere tendenze e modelli..

Pero incluso un modelo de Serie storicheUna serie temporale è un insieme di dati raccolti o misurati in tempi successivi, di solito a intervalli di tempo regolari. Questo tipo di analisi consente di identificare i modelli, Tendenze e cicli dei dati nel tempo. La sua applicazione è ampia, che coprono settori come l'economia, Meteorologia e sanità pubblica, facilitare la previsione e il processo decisionale basato su informazioni storiche.... tiene diferentes facetas. La maggior parte degli esempi che vediamo sul web riguardano serie temporali univariate. Sfortunatamente, I casi d'uso del mondo reale non funzionano in questo modo. Ci sono più variabili in gioco, e gestirli tutti allo stesso tempo è il punto in cui uno scienziato dei dati otterrà il suo coraggio.

In questo articolo, capiremo cos'è una serie storica multivariata e come affrontarla. Prenderemo anche un caso di studio e lo implementeremo in Python per darti una comprensione pratica dell'argomento..

Sommario

1. Serie temporali univariate e multivariate
   1. Serie temporali univariate
   2. Serie temporali multivariate
2. Gestione di una serie storica multivariata: regressione automatica vettoriale (DOVE)
3. Perché abbiamo bisogno di VAR?
4. Stazionarietà in una serie temporale multivariata
5. Divisione validazione treni
6. Implementazione Python

1. Serie temporali univariate e multivariate

Questo articolo presuppone una certa familiarità con le serie temporali univariate, le sue proprietà e le varie tecniche utilizzate per la previsione. Poiché questo articolo si concentrerà sulle serie temporali multivariate, Ti suggerisco di rivedere i seguenti articoli che servono come una buona introduzione alle serie temporali univariate:

Ma ti darò una rapida panoramica di cosa sia una serie temporale univariata., prima di entrare nei dettagli di una serie storica multivariata. Vediamoli uno per uno per capire la differenza.

1.1 Serie temporali univariate

Una serie temporale univariata, come suggerisce il nome, es una serie con una única variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... dipendente dal tempo.

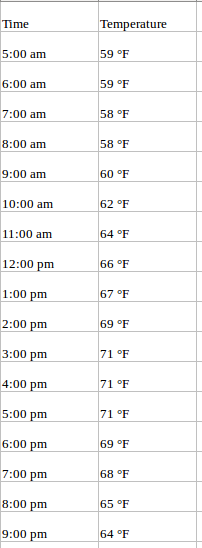
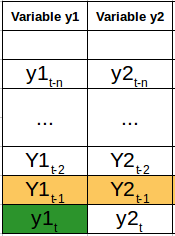
Ad esempio, dai un'occhiata al set di dati campione di seguito costituito dai valori di temperatura (ogni ora), durante l'ultimo 2 anni. Qui, la temperatura è la variabile dipendente (dipendente dal tempo).

Se ci viene chiesto di prevedere la temperatura per i prossimi giorni, guarderemo i valori passati e proveremo a misurare ed estrarre un modello. Avremmo notato che la temperatura è più bassa al mattino e alla sera, mentre raggiunge il picco nel pomeriggio. Cosa c'è di più, se hai dati degli ultimi anni, noterai che fa più freddo durante i mesi da novembre a gennaio, mentre è relativamente più caldo da aprile a giugno.

Tali osservazioni ci aiuteranno a prevedere i valori futuri.. Hai notato che usiamo solo una variabile? (la temperatura dell'ultimo 2 anni)? Perciò, questo si chiama Analisi / Previsione univariata delle serie temporali.

1.2 Serie temporali multivariate (MTS)

Una serie temporale multivariata ha più di una variabile dipendente dal tempo. Ogni variabile dipende non solo dai suoi valori passati, ha anche una certa dipendenza da altre variabili. Questa dipendenza viene utilizzata per prevedere i valori futuri. Sembra complicato? Lasciatemi spiegare.

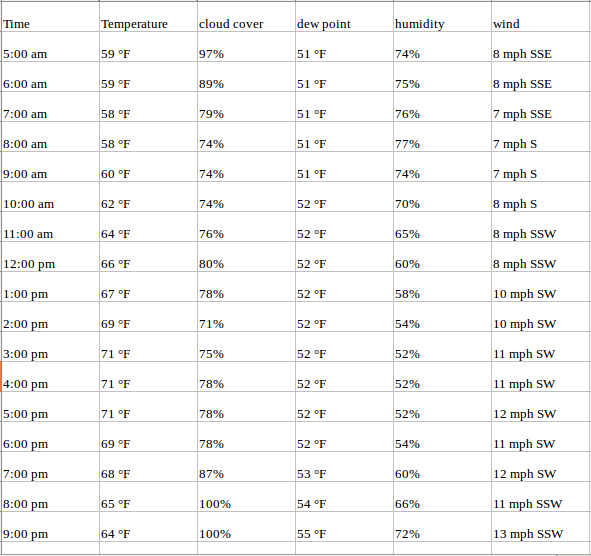
Considera l'esempio sopra. Supponiamo ora che il nostro set di dati includa la percentuale di sudorazione, punto di rugiada, velocità del vento, la percentuale di copertura nuvolosa, eccetera. insieme al valore della temperatura degli ultimi due anni. In questo caso, più variabili devono essere considerate per prevedere in modo ottimale la temperatura. Una serie come questa rientrerebbe nella categoria delle serie temporali multivariate.. Di seguito è riportata un'illustrazione di questo:

Ora che abbiamo capito come si presenta una serie temporale multivariata, capiamo come possiamo usarlo per costruire una previsione.

2. Gestione di una serie storica multivariata – DOVE

In questa sezione, Ti presenterò uno dei metodi più utilizzati per la previsione di serie temporali multivariate: Regressione automatica vettoriale (DOVE).

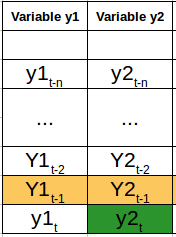
In un modello VAR, ogni variabile è una funzione lineare dei valori passati di se stessa e dei valori passati di tutte le altre variabili. Per spiegarlo meglio, Userò un semplice esempio visivo:

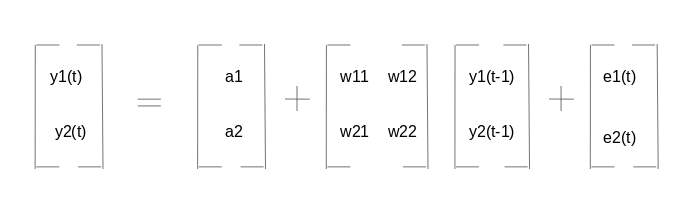
Abbiamo due variabili, y1 e y2. Dobbiamo prevedere il valore di queste due variabili al tempo t, dai dati forniti per gli n valori passati. Per semplificare, Ho preso il valore di ritardo per essere 1.

Per calcolare y1

Qui,

• a1 e a2 sono i termini costanti,
• w11, w12, w21 e w22 sono i coefficienti,
• e1 ed e2 sono i termini di errore

Queste equazioni sono simili all'equazione di un processo AR. Poiché il processo AR viene utilizzato per dati di serie temporali univariati, i valori futuri sono combinazioni lineari solo dei tuoi valori passati. Considera il processo AR (1):

e

In questo caso, abbiamo una sola variabile – e, un termine costante – un, un termine di errore – e, e un coefficiente – w. Per accogliere i termini variabili multipli in ogni equazione per VAR, useremo i vettori. Possiamo scrivere le equazioni (1) e (2) come segue:

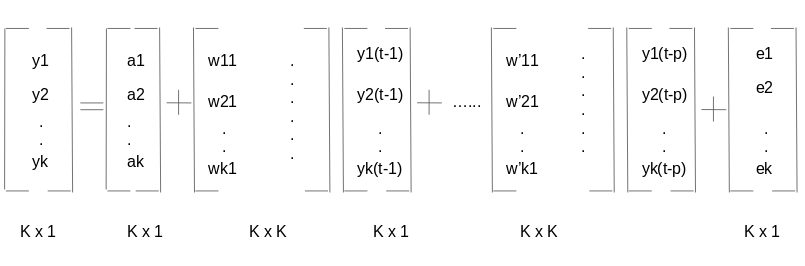
Le due variabili sono y1 e y2, seguito da una costante, un coefficiente metrico, un valore di ritardo e una metrica di errore. Questa è l'equazione vettoriale per un processo VAR (1). Per un processo VAR (2), un altro termine vettoriale verrà aggiunto per tempo (t-2) all'equazione da generalizzare per i ritardi:

L'equazione sopra rappresenta un processo VAR (P) con variabili y1, y2… yk. Lo stesso può essere scritto come:

Il termine_T nell'equazione rappresenta il rumore bianco vettoriale multivariato. Per una serie temporale multivariata, e_T deve essere un vettore casuale continuo che soddisfa le seguenti condizioni:

1. E (e_T) = 0
   Il valore atteso per il vettore di errore è 0
2. E (e_t1, e_t2') =₁₂
   Valore atteso di ε_T y_T'È la deviazione standard della serie?

3. Perché abbiamo bisogno di VAR?

Ricorda l'esempio della previsione delle temperature temperate che abbiamo visto prima. Si può sostenere che sarà trattata come una serie multipla univariata. Possiamo risolverlo usando semplici metodi di previsione univariata come AR. Poiché l'obiettivo è prevedere la temperatura, possiamo semplicemente rimuovere le altre variabili (tranne la temperatura) e adattare un modello alle restanti serie univariate.

Un'altra semplice idea è quella di prevedere singolarmente i valori di ogni serie utilizzando le tecniche che già conosciamo.. Questo renderebbe il lavoro estremamente facile!! Quindi, Perché dovrei imparare un'altra tecnica di previsione? Questo argomento non è già abbastanza complicato??

Dalle equazioni di cui sopra (1) e (2), è chiaro che ogni variabile utilizza i valori passati di ciascuna variabile per fare le previsioni. A differenza di AR, Il VAR è in grado di comprendere e utilizzare la relazione tra più variabili.. Questo è utile per descrivere il comportamento dinamico dei dati e fornisce anche migliori risultati di previsione.. Cosa c'è di più, implementare il VAR è semplice come usare qualsiasi altra tecnica univariata (cosa vedrai nell'ultima sezione).

4. Stazionarietà di una serie storica multivariata

Sappiamo dallo studio del concetto univariato che una serie storica stazionaria ci darà, Nella maggior parte dei casi, una migliore serie di previsioni. Se non hai familiarità con il concetto di stazionarietà, leggi prima questo articolo: Una delicata introduzione alla gestione di serie temporali non stazionarie.

Per riassumere, per una data serie storica univariata:

e

La serie si dice stazionaria se il valore di | C | <1. Ora, ricorda l'equazione del nostro processo VAR:

Nota: I è la matrice identità.

Rappresenta l'equazione in termini di Operatori di ritardo, avere:

Prendendo tutti i termini e

Il coefficiente di y

Perché una serie sia stazionaria, gli autovalori di | Phi (l)^-1| deve essere inferiore a 1 nel modulo. Questo può sembrare complicato dato il numero di variabili nella derivazione. Questa idea è stata spiegata da un semplice esempio numerico nel seguente video. Ti consiglio di guardarlo per consolidare la tua comprensione:

Simile al test Augmented Dickey-Fuller per serie univariate, abbiamo il test di Johansen per verificare la stazionarietà di qualsiasi dato di serie temporali multivariate. Vedremo come eseguire il test nell'ultima sezione di questo articolo.

5. Divisione validazione treni

Se in precedenza hai lavorato con dati di serie temporali univariati, conoscere i set di convalida del treno. L'idea di creare un set di convalida è analizzare le prestazioni del modello prima di utilizzarlo per fare previsioni..

Creare un set di convalida per problemi di serie temporali è complicato perché dobbiamo prendere in considerazione la componente temporale. Non si può usare direttamente il train_test_split oh k-fold convalida, in quanto ciò interromperà il modello nella serie. Il set di convalida deve essere creato tenendo presenti i valori di data e ora.

Supponiamo di dover prevedere la temperatura, punto di rugiada, la percentuale di nuvole, eccetera. per i prossimi due mesi utilizzando i dati degli ultimi due anni. Un metodo possibile è tenere da parte i dati degli ultimi due mesi e addestrare il modello nel 22 mesi rimanenti.

Una volta che il modello è stato addestrato, possiamo usarlo per fare previsioni sul set di convalida. Sulla base di queste previsioni e dei valori effettivi, possiamo controllare quanto bene ha funzionato il modello e le variabili per le quali il modello non ha funzionato altrettanto bene. E per fare la previsione finale, utilizzare l'intero set di dati (combinare treno e set di convalida).

6. Implementazione Python

In questa sezione, implementeremo il modello Vector AR in un set di dati giocattolo. Ho usato il set di dati sulla qualità dell'aria per questo e puoi scaricarlo da qui.

#importare i pacchetti richiesti
importa panda come pd
importa matplotlib.pyplot come plt
%matplotlib in linea

#leggi i dati
df = pd.read_csv("AirQualityUCI.csv", parse_dates=[['Data', 'Tempo']])

#controlla i dtypes
df.dtypes

Oggetto Date_Time
CO(GT)            int64
PT08.S1(CO)       int64
NMHC(GT)          int64
C6H6(GT)          int64
PT08.S2(NMHC)     int64
NOx(GT)           int64
PT08.S3(NOx)      int64
NO2(GT)           int64
PT08.S4(NO2)      int64
PT08.S5(O3)       int64
T int64
RH int64
AH int64
dtype: oggetto

Il tipo di dati di Data e ora la colonna è oggetto e dobbiamo cambiarlo in Data e ora. Cosa c'è di più, per preparare i dati, necesitamos que el indiceIl "Indice" È uno strumento fondamentale nei libri e nei documenti, che consente di individuare rapidamente le informazioni desiderate. In genere, Viene presentato all'inizio di un'opera e organizza i contenuti in modo gerarchico, compresi capitoli e sezioni. La sua corretta preparazione facilita la navigazione e migliora la comprensione del materiale, rendendolo una risorsa essenziale sia per gli studenti che per i professionisti in vari settori.... tenga Data e ora. Segui i seguenti comandi:

df['Appuntamento'] = pd.to_datetime(df.Date_Time , formato="%d/%m/%Y %H.%M.%S")
data = df.drop(['Appuntamento'], asse=1)
data.index = df.Date_Time

Il prossimo passo è occuparsi dei valori mancanti. Poiché i valori mancanti nei dati vengono sostituiti con un valore -200, dovremo imputare il valore mancante con un numero migliore. Considera questo: se manca il valore attuale del punto di rugiada, possiamo tranquillamente presumere che sarà vicino al valore dell'ora precedente. Ha senso, verità? Qui, io imputerò -200 con il valore precedente.

Puoi scegliere di sostituire il valore utilizzando la media di alcuni valori precedenti, oppure il valore alla stessa ora del giorno prima (puoi condividere la tua (S) idea (S) imputare i valori mancanti nella sezione commenti qui sotto).

#trattamento del valore mancante
cols = data.columns
per j in cols:
    per io nel raggio d'azione(0,len(dati)):
       se i dati[J][io] == -200:
           dati[J][io] = dati[J][i-1]

#controllo della stazionarietà
da statsmodels.tsa.vector_ar.vecm import coint_johansen
#dal momento che il test funziona solo per 12 variabili, Ho lasciato cadere a caso
#nella prossima iterazione, Ne lascerei un altro e controllerei gli autovalori
johan_test_temp = data.drop([ 'CO(GT)'], asse=1)
coint_johansen(johan_test_temp,-1,1).possedere

Di seguito è riportato il risultato del test:

Vettore([ 0.17806667,  0.1552133 ,  0.1274826 ,  0.12277888,  0.09554265,
        0.08383711,  0.07246919,  0.06337852,  0.04051374,  0.02652395,
        0.01467492,  0.00051835])

Ora possiamo andare avanti e creare il set di convalida per adattare il modello e testare le prestazioni del modello:

#creazione del treno e set di convalida
treno = dati[:int(0.8*(len(dati)))]
valido = dati[int(0.8*(len(dati))):]

#adatta al modello
da statsmodels.tsa.vector_ar.var_model import VAR

modello = VAR(endog = treno)
model_fit = model.fit()

# fare previsioni sulla convalida
previsione = model_fit.forecast(model_fit.y, passi = len(valido))

Le previsioni sono sotto forma di matrice, dove ogni elenco rappresenta le previsioni nella riga. Lo trasformeremo in un formato più presentabile.

#convertire le previsioni in dataframe
pred = pd.DataFrame(indice=intervallo(0,len(predizione)),colonne=[cols])
per j nell'intervallo(0,13):
    per io nel raggio d'azione(0, len(predizione)):
       pred.iloc[io][J] = previsione[io][J]

#controlla rmse
per io in cols:
    Stampa('valore efficace per', io, 'è : ', sqrt(mean_squared_error(pred[io], valido[io])))

Uscita codice precedente:

valore efficace per CO(GT) è :  1.4200393103392812
Valore efficace per PT08.S1(CO) è :  303.3909208229375
valore efficace per NMHC(GT) è :  204.0662895081472
valore efficace per C6H6(GT) è :  28.153391799471244
Valore efficace per PT08.S2(NMHC) è :  6.538063846286176
valore efficace per NOx(GT) è :  265.04913993413805
Valore efficace per PT08.S3(NOx) è :  250.7673347152554
valore efficace per NO2(GT) è :  238.92642219826683
Valore efficace per PT08.S4(NO2) è :  247.50612831072633
Valore efficace per PT08.S5(O3) è :  392.3129907890131
Il valore efficace per T è :  383.1344361254454
Il valore efficace per RH è :  506.5847387424092
Il valore efficace per AH è :  8.139735443605728

Dopo il test nel set di convalida, adattiamo il modello al set di dati completo

#fare previsioni finali
modello = VAR(pari = dati)
model_fit = model.fit()
yhat = model_fit.forecast(model_fit.y, passi=1)
Stampa(sì)

Note finali

Prima di iniziare questo articolo, l'idea di lavorare con una serie temporale multivariata sembrava scoraggiante nella portata. È una questione complessa, quindi prenditi il ​​tuo tempo per capire i dettagli. Il modo migliore per imparare è fare pratica, quindi spero che l'implementazione di Python sopra ti sia utile.

Ti consiglio di utilizzare questo approccio su un set di dati di tua scelta. Ciò rafforzerà ulteriormente la tua comprensione di questo argomento complesso ma molto utile.. Se hai suggerimenti o domande, condividilo nella sezione commenti.

Imparentato