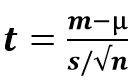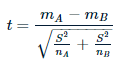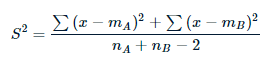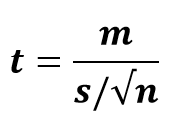introduzione
"Non puoi testare un'ipotesi; puoi solo migliorarlo o confutarlo “. – Christopher Monckton
Ogni giorno ci troviamo a provare nuove idee, trovare il percorso più veloce per l'ufficio, il modo più veloce per finire il nostro lavoro o semplicemente trovare un modo migliore per fare qualcosa che amiamo. La domanda critica, poi, è se la nostra idea è significativamente migliore di quella che abbiamo testato in precedenza.
Queste idee che ci vengono così regolarmente, questo è essenzialmente ciò che è un'ipotesi. E prova queste idee per scoprire quale funziona e quale è meglio lasciare indietro., si chiama test di ipotesi.
Il test di ipotesi è una delle cose più affascinanti che facciamo come scienziati dei dati. Nessuna idea è off limits in questa fase del nostro progetto. Personalmente, Ho visto molte idee emerse dalla verifica delle ipotesi, Idee che molti di noi avrebbero perso se non fosse stato per questa fase!!
Uno dei modi più popolari per testare un'ipotesi è un concetto chiamato test t.. Esistono diversi tipi di t-test, come vedremo presto, e ognuno ha la sua applicazione unica. Se sei un aspirante scienziato dei dati, devi sapere cos'è un t-test e quando puoi trarne vantaggio.
Quindi, in questo articolo, Impareremo le varie sfumature di un t-test e poi esamineremo i tre diversi tipi di t-test.. Ciliegina sulla torta? Implementeremo ogni tipo di t-test in R per visualizzare come funzionano in scenari pratici. Andiamo!
Nota: dovresti leggere l'articolo qui sotto se hai bisogno di rispolverare i concetti di test di ipotesi:
Sommario
- Quando dovremmo eseguire un t-test?
- Ipotesi per l'esecuzione di un t-test
- Tipi di test t (con esempi elaborati in R)
- T-test per un campione
- T-test indipendente per due campioni
- Campioni appaiati t test
Quando dovremmo eseguire un t-test?
Per prima cosa capiamo dove può essere utilizzato un t-test prima di immergerci nei suoi diversi tipi e implementazioni.. Credo fermamente che il modo migliore per imparare un concetto sia visualizzarlo attraverso un esempio. Quindi facciamo un semplice esempio per vedere dove torna utile un t-test.
Considera un'azienda di telecomunicazioni che ha due centri servizi in città. L'azienda vuole sapere se il tempo medio necessario per servire un cliente è lo stesso in entrambi i negozi.
Fonte: Shopworks
L'azienda misura il tempo medio impiegato 50 clienti casuali in ogni negozio. Il negozio A prende 22 minuti, mentre il negozio B ha una media di 25 minuti. Possiamo dire che il negozio A è più efficiente del negozio B in termini di servizio clienti?
Sembra così, no? tuttavia, abbiamo solo analizzato 50 clienti casuali delle tante persone che visitano i negozi. Il semplice esame del tempo medio di campionamento potrebbe non essere rappresentativo di tutti i clienti che visitano entrambi i negozi.
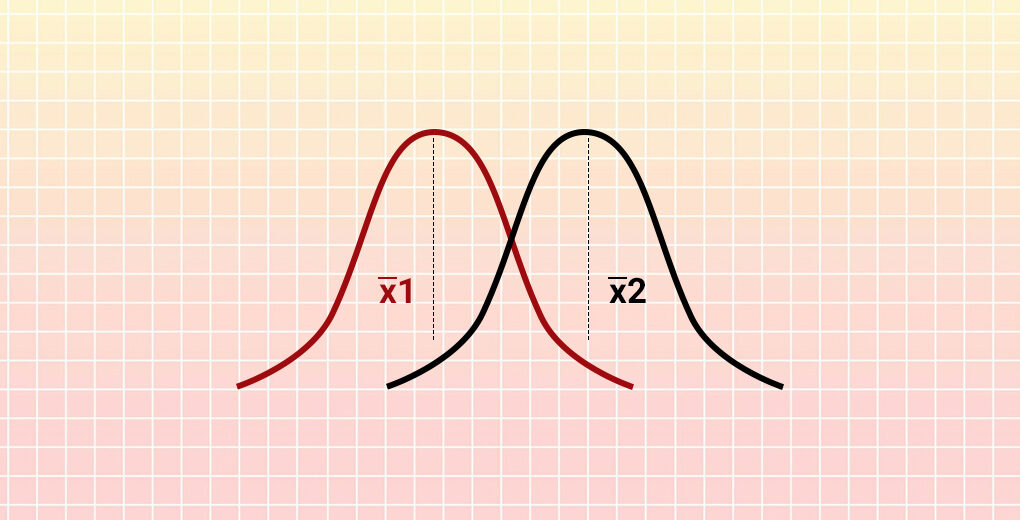
È qui che entra in gioco il t-test.. Ci aiuta a capire se la differenza tra due medie campione è davvero reale o è semplicemente dovuta al caso.
Ipotesi per l'esecuzione di un t-test
Ci sono alcune ipotesi che dobbiamo prendere in considerazione prima di condurre un t-test.:
- I dati devono seguire una scala continua o ordinale (punteggi dei test del QI degli studenti, ad esempio)
- Le osservazioni nei dati dovrebbero essere selezionate casualmente
- I dati dovrebbero apparire come una curva a campana quando vengono tracciati, vale a dire, dovrebbe essere distribuito normalmente. Puoi fare riferimento a questo articolo per capire meglio la distribuzione normale
- È necessario prendere un campione di grandi dimensioni per avvicinare i dati a una distribuzione normale (unsebbene il t-test sia essenziale per piccoli campioni poiché le sue distribuzioni non sono normali)
- Le variazioni tra i gruppi devono essere uguali (Fo test t indipendente su due campioni)
Quindi, Quali sono i diversi tipi di t test? Quando dovremmo eseguire ogni tipo?? Risponderemo a queste domande nella prossima sezione e vedremo come possiamo eseguire ogni tipo di t-test in R.
Tipi di test t (con esempi elaborati in R)
Esistono tre tipi di t-test che possiamo eseguire in base ai dati disponibili:
- t-test per un campione
- T-test indipendente su due campioni
- Campioni appaiati t test
In questa sezione, vedremo ciascuno di questi tipi in dettaglio. Ho anche fornito il codice R per ogni tipo di t-test in modo che tu possa seguirli mentre li implementiamo. È un ottimo modo per imparare e vedere quanto sono utili questi t-test!!
T-test per un campione
In un t-test di un campione, confrontiamo la media (o media) di un gruppo con la media (o media) sistemato. Questa media stabilita può essere qualsiasi valore teorico (oppure può essere la media della popolazione).
Considera il seguente esempio: un ricercatore vuole determinare se il tempo medio per mangiare un hamburger (taglia standard) differisce da un valore impostato. Diciamo che questo valore è 10 minuti. Come pensi che il ricercatore possa determinarlo??
Lui / può seguire ampiamente i seguenti passaggi:
- Seleziona un gruppo di persone
- Registra il tempo di assunzione individuale di un hamburger di dimensioni standard.
- Calcola il tempo medio dei pasti del gruppo.
- Finalmente, confrontare quel valore medio con il valore impostato di 10
In poche parole, ecco come possiamo eseguire un t-test di un campione. Ecco la formula per calcolarlo:
dove,
- t = t statistica
- m = media di gruppo
- µ = valore teorico o media della popolazione
- s = deviazione standard del gruppo
- n = dimensione del gruppo o dimensione del campione
Nota: Come accennato in precedenza nelle ipotesi che deve essere presa una grande dimensione del campione affinché i dati si avvicinino a una distribuzione normale. (Sebbene il t-test sia essenziale per piccoli campioni poiché le sue distribuzioni non sono normali).
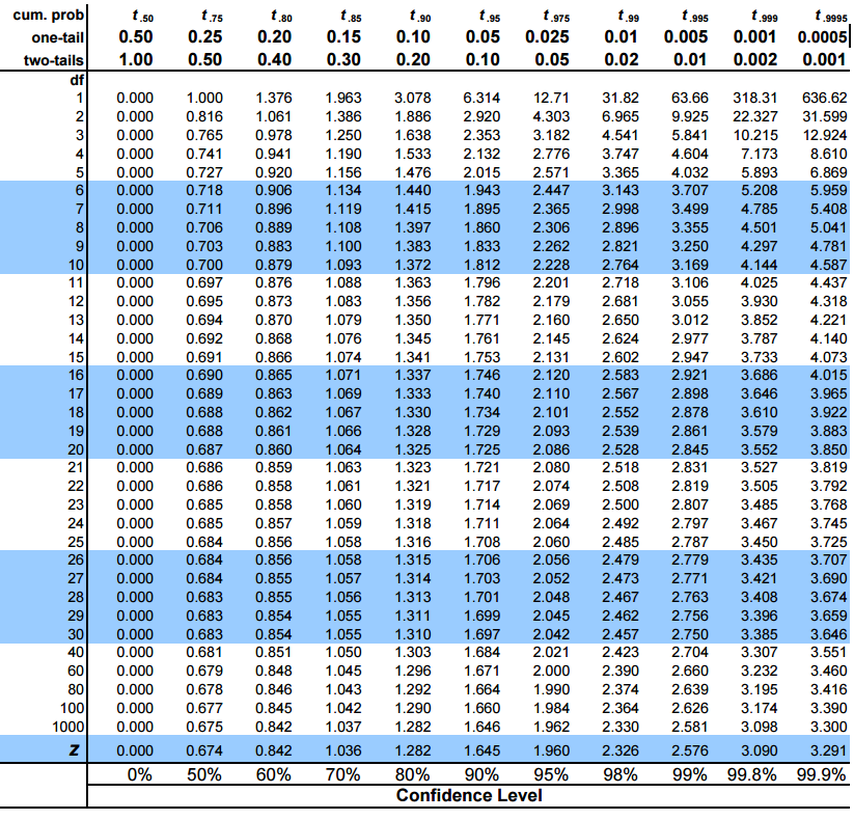
Una volta calcolato il valore della statistica t, il prossimo compito è confrontarlo con il valore critico del t-test. Possiamo trovarlo nella seguente tabella del test t rispetto al grado di libertà (n-1) e il livello di significatività:
Questo metodo ci aiuta a verificare se la differenza tra le medie è statisticamente significativa o meno.. Consolidiamo ulteriormente la nostra comprensione di un t-test a un campione eseguendolo su R.
Implementazione del t-test a un campione in R
Un'azienda produttrice di telefoni cellulari ha prelevato un campione di telefoni cellulari dello stesso modello dai dati del mese precedente. Vogliono verificare se la dimensione media dello schermo del campione differisce dalla lunghezza desiderata di 10 cm. Puoi scaricare i dati qui.
passo 1: Primo, importare i dati.
passo 2: Convalida per essere corretto in R:
Produzione:
#Conteggio di righe e colonne
[1] 1000 1
> #Visualizza in alto 10 rows of the dataset
Screen_size.in.cm.
1 10.006692
2 10.081624
3 10.072873
4 9.954496
5 9.994093
6 9.952208
7 9.947936
8 9.988184
9 9.993365
10 10.016660
passo 3: Ricordate le ipotesi di cui abbiamo discusso prima?? Dobbiamo rivederli:
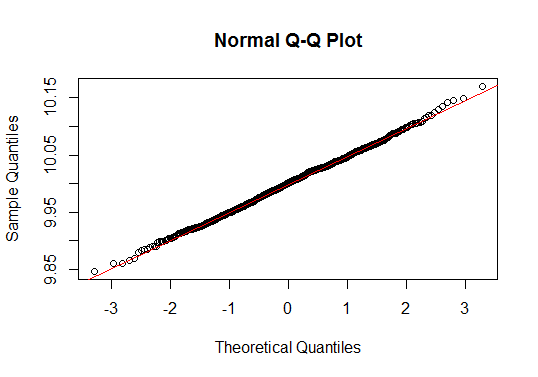
Otteniamo il seguente grafico QQ:
Quasi tutti i valori sono sulla linea rossa. Possiamo tranquillamente dire che i dati seguono una distribuzione normale.
passo 4: Eseguire un t-test di un campione:
Produzione:
One Sample t-test
data: data$Screen_size.in.cm.
t = -0.39548, df = 999, p-valore = 0.6926
ipotesi alternativa: la media vera non è uguale a 10
95 intervallo di confidenza percentuale:
9.996361 10.002418
stime campione:
media di x
9.99939La statistica t risulta essere -0,39548. Nota che qui possiamo trattare i valori negativi come la loro controparte positiva. Ora, fare riferimento alla tabella sopra menzionata per il valore t critico. Il grado di libertà qui è 999 e l'intervallo di confidenza è 95%.
Il valore t-critico è 1,962. Poiché la statistica t è inferiore al valore critico t, no rechazamos la ipotesi nullaL'ipotesi nulla è un concetto fondamentale in statistica che stabilisce un'affermazione iniziale su un parametro di popolazione. Il suo scopo è quello di essere testato e, se confutato, ci permette di accettare l'ipotesi alternativa. Questo approccio è essenziale nella ricerca scientifica, in quanto fornisce un quadro di riferimento per valutare le prove empiriche e prendere decisioni basate sui dati. La sua formulazione e analisi sono cruciali negli studi statistici.... y podemos concluir que el tamaño de pantalla promedio de la muestra no difiere de 10 cm.
Possiamo anche verificarlo dal p-value, che è maggiore di 0.05. Perciò, non rifiutiamo l'ipotesi nulla in un intervallo di confidenza di 95%.
T-test indipendente su due campioni
Il test t su due campioni viene utilizzato per confrontare le medie di due campioni diversi.
Diciamo di voler confrontare l'altezza media dei dipendenti di sesso maschile con l'altezza media delle donne. Certo, il numero di maschi e femmine dovrebbe essere uguale per questo confronto. Qui è dove viene utilizzato un t-test a due campioni.
Ecco la formula per calcolare la statistica t per un test t a due campioni:
dove,
- MetroUN y MB sono le medie di due campioni diversi
- NordUN e nB sono le dimensioni del campione?
- S2 è un stimatoreIl "Estimatore" è uno strumento statistico utilizzato per dedurre le caratteristiche di una popolazione da un campione. Si basa su metodi matematici per fornire stime accurate e affidabili. Esistono diversi tipi di stimatori, come l'imparzialità e la coerenza, che vengono scelti in base al contesto e all'obiettivo dello studio. Il suo corretto utilizzo è essenziale nella ricerca scientifica, Sondaggi e analisi dei dati.... de la varianza común de dos muestras, Che cosa:
Qui, il grado di libertà è nUN + nB – 2.
Seguiremo la stessa logica che abbiamo visto in un test t per un campione per verificare se la media di un gruppo è significativamente diversa da un altro gruppo.. Ecco com'è, confronteremo la statistica t calcolata con il valore t critico.
Facciamo un esempio di un test t indipendente su due campioni e risolviamolo in R.
Implementazione del t-test a due campioni in R
Per questa sezione, lavoreremo con i dati su due campioni dei diversi modelli di telefono cellulare. Vogliamo verificare se la dimensione media dello schermo del campione 1 differisce dalla dimensione media dello schermo del campione 2. Puoi scaricare i dati qui.
passo 1: Ancora, prima importa i dati.
passo 2: Convalida per essere corretto in R:
passo 3: Dobbiamo verificare le ipotesi come abbiamo fatto sopra. Lascio questo esercizio nelle tue mani ora.
Cosa c'è di più, in questo caso, verificheremo l'omogeneità della varianza:
Produzione:
#Omogeneità della varianza > dove(data$screensize_sample1) [1] 0.00238283 > dove(dati$screensize_sample2) [1] 0.002353585
Fantastico, le variazioni sono uguali. Possiamo andare avanti.
passo 4: Eseguire il t-test di due campioni indipendenti:
Nota: Riscrivere il codice precedente con "var.equal = f" se si ottengono variazioni irregolari o sconosciute. Questo sarà un caso di T-test di Welch che viene utilizzato per confrontare le medie di due campioni con varianze disuguali.
Produzione:
Two Sample t-test data: data$screensize_sample1 and data$screensize_sample2 t = 1.3072, df = 1998, p-valore = 0.1913 ipotesi alternativa: la vera differenza di mezzi non è uguale a 0 95 intervallo di confidenza percentuale: -0.001423145 0.007113085 stime campione: media di x media di y 10.000976 9.998131
Cosa puoi dedurre dal risultato di cui sopra? Possiamo confermare che la statistica t è di nuovo inferiore al valore critico t, quindi non rifiutiamo l'ipotesi nulla. Perciò, possiamo concludere che non vi è alcuna differenza tra la dimensione media dello schermo di entrambi i campioni.
Possiamo controllarlo di nuovo usando il valore p. Risulta essere maggiore di 0.05, così, non rifiutiamo l'ipotesi nulla in un intervallo di confidenza di 95%. Non vi è alcuna differenza tra la media dei due campioni.
Campioni appaiati t test
Il t-test dei campioni appaiati è piuttosto intrigante. Qui, misuriamo un gruppo in due momenti diversi. Confrontiamo mezzi separati per un gruppo in due momenti diversi o in due condizioni diverse. Confuso? Lasciatemi spiegare.
Un certo manager ha notato che il livello di produttività dei suoi dipendenti tendeva significativamente al ribasso. Questo manager ha deciso di realizzare un programma di formazione per tutti i suoi dipendenti al fine di aumentare i loro livelli di produttività.
In che modo il manager misurerà se i livelli di produttività sono aumentati?? È semplice: basta confrontare il livello di produttività dei dipendenti prima e dopo il programma di formazione.
Qui, confrontiamo lo stesso campione (gli impiegati) in due momenti diversi (prima e dopo l'allenamento). Questo è un esempio di test t accoppiato. La formula per calcolare la statistica t per un test t appaiato è:
dove,
- t = t statistica
- m = media di gruppo
- µ = valore teorico o media della popolazione
- s = deviazione standard del gruppo
- n = dimensione del gruppo o dimensione del campione
Possiamo prendere il grado di libertà in questo test come n – 1 visto che è coinvolto un solo gruppo. Ora, risolviamo un esempio in R.
Implementazione del test t appaiato in R
Il manager di un'azienda produttrice di pneumatici vuole confrontare il materiale in gomma di due lotti di pneumatici. Un modo per farlo: controllare la differenza tra i chilometri medi percorsi da un lotto di pneumatici fino all'usura.
Puoi scaricare i dati da qui. capito!
passo 1: Primo, importare i dati.
passo 2: Convalida per essere corretto in R:
passo 3: Ora controlliamo le ipotesi proprio come abbiamo fatto in un t-test a campione. Ancora, lo lascio a te.
passo 4: Eseguire il test t accoppiato:
Produzione:
Paired t-test data: data$tyre_1 and data$tyre_2 t = -5.2662, df = 24, valore p = 2.121e-05 ipotesi alternativa: la vera differenza di mezzi non è uguale a 0 95 intervallo di confidenza percentuale: -2201.6929 -961.8515 stime campione: media delle differenze -1581.772
Devi essere un esperto nel decifrare questo output a questo punto!! Il valore p è minore di 0.05. Possiamo rifiutare l'ipotesi nulla con un intervallo di confidenza di 95% e concludere che esiste una differenza significativa tra le medie dei pneumatici prima e dopo la sostituzione del materiale in gomma.
La media negativa della differenza mostra che i chilometri medi percorsi dal pneumatico 2 sono superiori alla media dei chilometri percorsi dal pneumatico 1.
Note finali
In questo articolo, abbiamo imparato il concetto di t-test, le sue ipotesi e anche i tre diversi tipi di t-test con le loro implementazioni in R. Il t-test ha sia un significato statistico che applicazioni pratiche nel mondo reale.. .
Se non conosci le statistiche, vuoi coprire le tue basi e vuoi anche iniziare nella scienza dei dati, Ti consiglio di prendere il Corso introduttivo alla scienza dei dati. Ti offre una panoramica completa delle statistiche descrittive e inferenziali prima di immergerti nelle tecniche di data science.
Hai trovato questo articolo utile? Ti vengono in mente altre applicazioni del t-test?? Fatemi sapere nella sezione commenti qui sotto e possiamo avere più idee!!
