Statistiche degli ordini | Cosa sono le statistiche sugli ordini??

introduzione

La statistica degli ordini è un concetto molto utile nella scienza statistica. Hanno una vasta gamma di applicazioni, inclusa la modellazione delle aste, auto da corsa e polizze assicurative, ottimizzazione dei processi produttivi, Stima di parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... di distribuzioni, et al. Attraverso questo articolo, capiremo l'idea delle statistiche degli ordini. Prima capiremo il suo significato e gradualmente procederemo alla sua distribuzione., eventualmente coprendo concetti più avanzati.

Supponiamo di avere un insieme di variabili casuali X₁, X₂, …, X_Nord, indipendenti e identicamente distribuiti (iid). Per l'indipendenza, intendiamo che il valore assunto da un variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... non è influenzato dai valori assunti da altre variabili aleatorie. Per distribuzione identica, intendiamo che la funzione di densità di probabilità (PDF) (o equivalente, la funzione di distribuzione cumulativa, CDF) per le variabili casuali è lo stesso. il K^ns La statistica dell'ordine per questo insieme di variabili casuali è definita come k^ns valore del campione più piccolo.

Per capire meglio questo concetto, prenderemo 5 variabili casuali X₁, X₂, X₃, X₄, X₅. Osserveremo una realizzazione / risultato casuale della distribuzione di ciascuna di queste variabili casuali. Supponiamo di ottenere i seguenti valori:

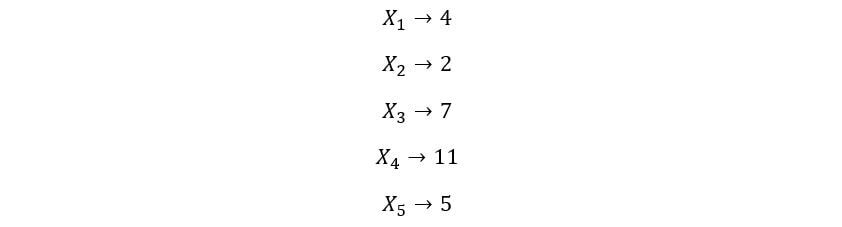
il K^ns la statistica dell'ordine per questo esperimento è k^ns valore più piccolo dell'insieme {4, 2, 7, 11, 5}. Quindi, il 1^Ns la statistica dell'ordine è 2 (valore minimo), il 2^{Nord Dakota} la statistica dell'ordine è 4 (il prossimo più piccolo), e così via. Il 5^ns la statistica dell'ordine è il quinto valore più piccolo (il valore più grande), Che cos'è 11. Ripetiamo questo processo molte volte, vale a dire, estraiamo campioni dalla distribuzione di ciascuna di queste variabili casuali iid e troviamo il k^ns valore minimo per ogni insieme di osservazioni. La distribuzione di probabilità di questi valori dà la distribuzione di k^ns statistiche degli ordini.

Generalmente, se ordiniamo variabili casuali X₁, X₂, …, X_Nord in ordine crescente, poi il k^ns la statistica dell'ordine viene visualizzata come:

La notazione generale del k^ns la statistica dell'ordine è X_(K). Nota X_(K) è diverso da X_K. X_K è il k^ns variabile casuale del nostro insieme, mentre X_(K) è il k^ns ordine statistico del nostro insieme. X_(K) assume il valore di X_K si X_K è il k^ns Variabile casuale quando le realizzazioni sono ordinate in ordine crescente.

Il 1^Ns Statistica dell'ordine X₍₁₎ è l'insieme dei valori minimi della realizzazione dell'insieme di 'n’ variabili casuali. Dopo^ns Statistica dell'ordine X_(Nord) è l'insieme dei valori massimi (ennesimo valore minimo) della realizzazione dell'insieme di 'n’ variabili casuali. Possono essere espressi come:

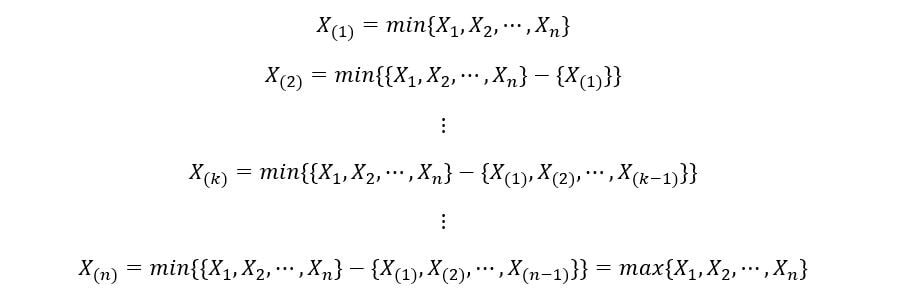
Distribuzione delle statistiche degli ordini

Ora proveremo a scoprire la distribuzione delle statistiche dell'ordine. Descriveremo prima la distribuzione di n^ns statistiche degli ordini, poi lui 1^Ns ordine statistico e infine il k^ns statistiche generali sull'ordine.

UN) Distribuzione di n^ns Statistiche degli ordini:

Sia la funzione di densità di probabilità (PDF) e la funzione di distribuzione cumulativa (CDF) le nostre variabili casuali lasciano f_X(X) y F_X(X) rispettivamente. Per definizione di CDF,

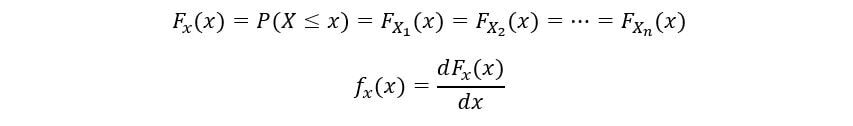
Poiché le nostre variabili casuali sono distribuite in modo identico, avere lo stesso PDF f_X(X) y CDF F_X(X). Ora calcoleremo il CDF di n^ns statistiche degli ordini (F_Nord(X)) come segue:

Variabili casuali X₁, X₂, …, X_Nord sono anche indipendenti. Perciò, per proprietà di indipendenza,

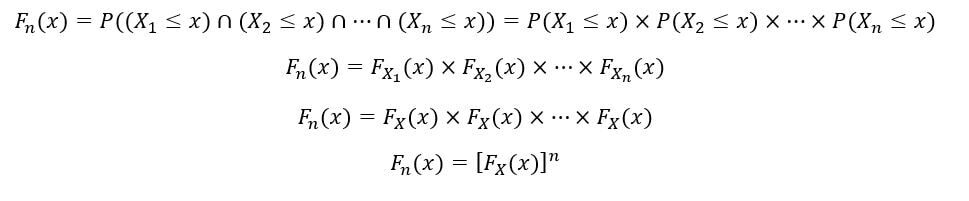
Il PDF del n^ns ordine statistico (F_Nord(X)) è calcolato come segue:

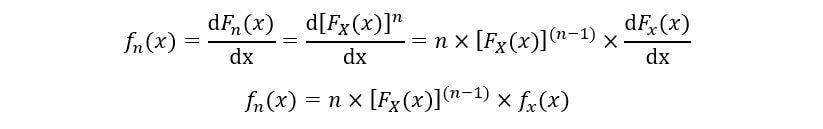
Perciò, l'espressione per PDF e CDF di n^ns La statistica dell'ordine è stata ottenuta.

B) Distribuzione di 1^Ns Statistiche degli ordini:

Il CDF di una variabile casuale può anche essere calcolato come quello meno la probabilità che la variabile casuale X assuma un valore maggiore o uguale a x. Matematicamente,

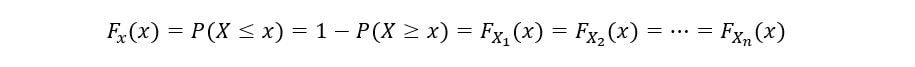
Determinare il CDF di 1^Ns statistiche degli ordini (F₁(X)) come segue:

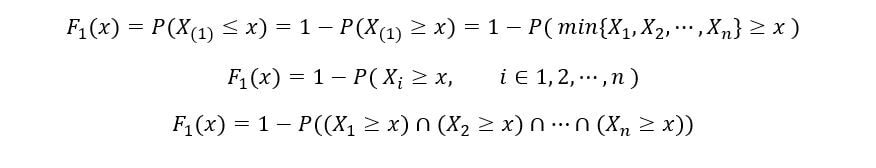
Un'altra volta, usando la proprietà di indipendenza delle variabili casuali,

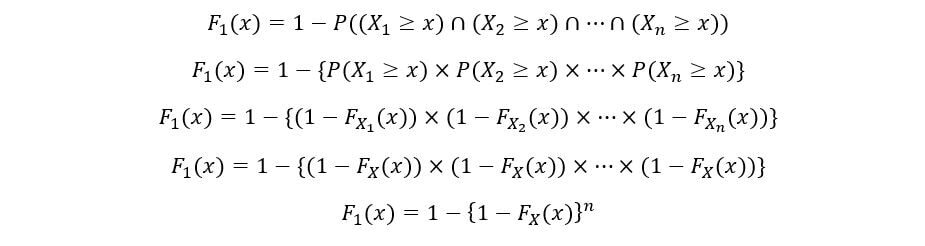
Il PDF del 1^Ns ordine statistico (F₁(X)) è calcolato come segue:

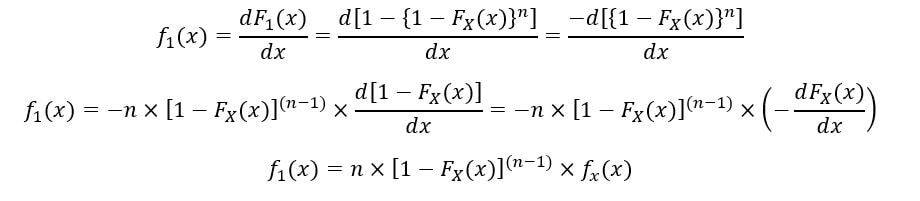
Perciò, l'espressione per PDF e CDF di 1^Ns La statistica dell'ordine è stata ottenuta.

C) Distribuzione del k^ns Statistiche degli ordini:

Forchetta^ns statistiche degli ordini, generalmente, la seguente equazione descrive il tuo CDF (F_K(X)):

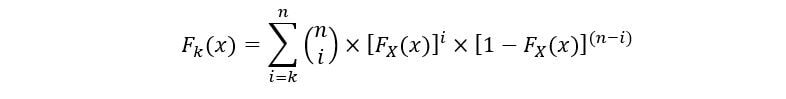
Il PDF di k^ns ordine statistico (F_K(X)) è espresso come:

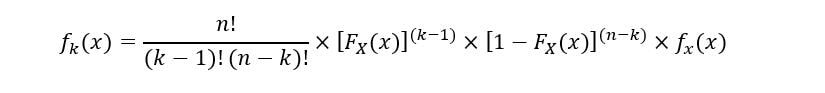
Per evitare confusioni, useremo prove geometriche per capire l'equazione. Come discusso sopra, l'insieme delle variabili casuali ha lo stesso PDF (F_X(X)). Il grafico seguente mostra un PDF di esempio con il k^ns Statistica dell'ordine ottenuta da campionamento casuale:

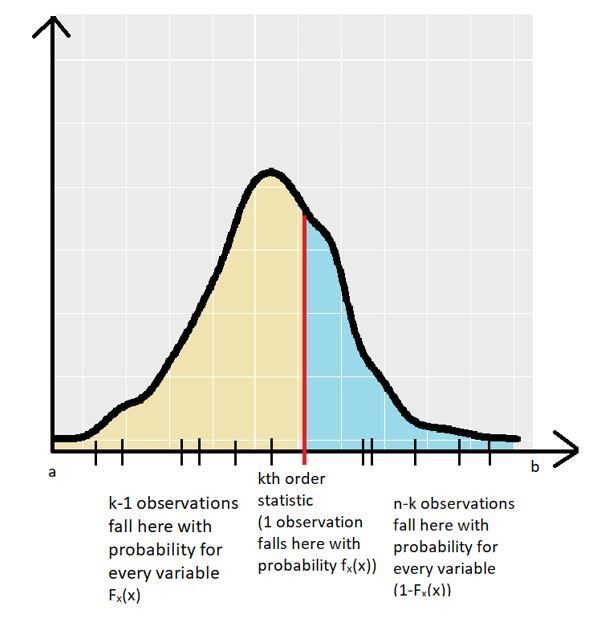
Quindi, il PDF delle variabili casuali f_X(X) è definito tra l'intervallo [un,B]. La statistica dell'ordine k-esimo per un campione casuale è mostrata con la linea rossa. Le altre realizzazioni variabili (per il campione casuale) mostrato dalle piccole linee nere sull'asse x.

Ci sono esattamente (K – 1) osservazioni di variabili casuali che cadono nella regione gialla del grafico (la regione tra & K^ns statistiche degli ordini). La probabilità che una particolare osservazione rientri in questa regione è data dal CDF delle variabili casuali (F_X(X)). Ma siamo consapevoli che (K – 1) le osservazioni sono diminuite nella regione, cosa ci dà il termine (per l'indipendenza) (F_X(X))^{(K – 1)}.

Ci sono esattamente (n – K) osservazioni di variabili casuali che cadono nella regione blu del grafico (la regione tra k^ns ordine statistico & B). La probabilità che una particolare osservazione cada in questa regione è data dal 1 – CDF delle variabili casuali (1- F_X(X)). Ma siamo consapevoli che (n – K) le osservazioni sono diminuite nella regione, cosa ci dà il termine (per l'indipendenza) (1-F_X(X))^{(n – K)}.

Finalmente, Esattamente 1 l'osservazione cade esattamente sulla statistica di ordine k-esimo con probabilità f_X(X). Perciò, il prodotto di 3 termini ci dà un'idea del significato geometrico dell'equazione per PDF della statistica di ordine k-esimo. Ma, Da dove viene il termine fattoriale?? Lo scenario di cui sopra ha mostrato solo uno dei tanti ordini. Ci possono essere molte di queste combinazioni. Il numero totale di tali combinazioni è mostrato di seguito:

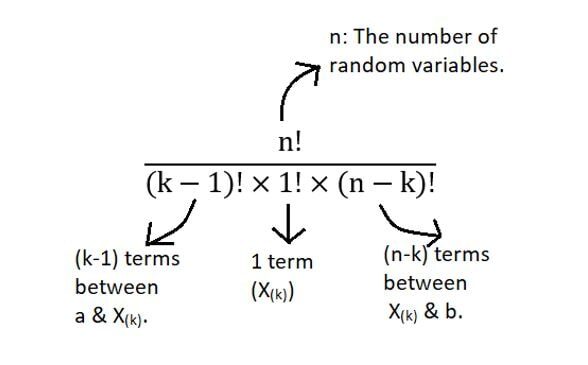
Perciò, il prodotto di tutti questi termini ci dà la distribuzione generale di k^ns statistiche degli ordini.

Utili funzioni di statistica ordini

Le statistiche degli ordini portano a diverse funzioni utili. Tra loro, Tra le più importanti vi sono l'intervallo del campione e il medianoLa mediana è una misura statistica che rappresenta il valore centrale di un insieme di dati ordinati. Per calcolarlo, I dati sono organizzati dal più basso al più alto e viene identificato il numero al centro. Se c'è un numero pari di osservazioni, I due valori fondamentali sono mediati. Questo indicatore è particolarmente utile nelle distribuzioni asimmetriche, poiché non è influenzato da valori estremi.... del campione.

1) Gamma di campioni: È definita come la differenza tra il valore più grande e il più piccolo. Si esprime come segue:

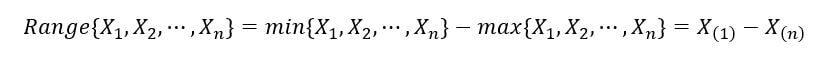
2) Mediana del campione: La mediana campionaria divide il campione casuale (realizzazioni dell'insieme delle variabili casuali) in due metà, uno contenente i campioni di valore più basso e l'altro contenente i campioni di valore più alto. È come la statistica dell'ordine medio / centrale. È matematicamente definito come:

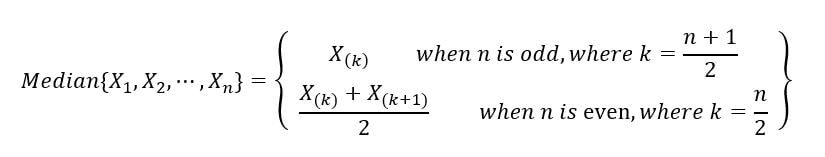
Set di statistiche sugli ordini PDF

Una funzione di densità di probabilità congiunta può aiutarci a comprendere meglio la relazione tra due variabili casuali (statistiche a due ordini
nel nostro caso). Il PDF congiunto per qualsiasi statistica di 2 X ordini_(un) & X_(B), tale che 1 ≤ a ≤ b ≤ n è dato dalla seguente equazione:

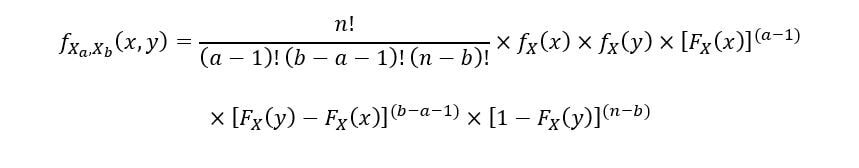
Esempio

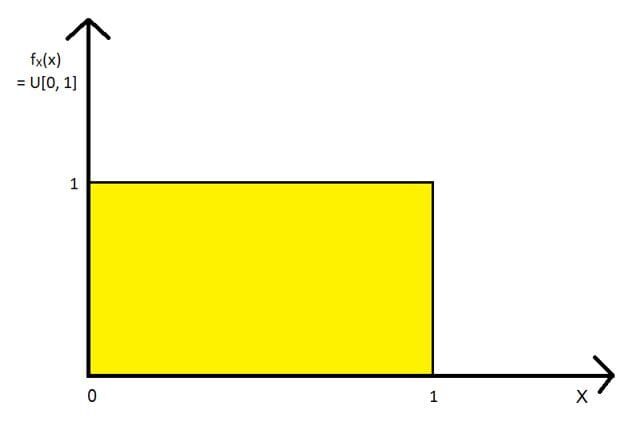
Useremo un esempio molto semplice per illustrare la distribuzione delle statistiche dell'ordine: la distribuzione uniforme standard (tu[0, 1] distribuzione). noi prenderemo 5 variabili casuali X₁, X₂, X₃, X₄, X₅, tutti hanno l'U[0, 1] distribuzione. Per questo insieme di variabili casuali, calcoleremo e disegneremo il 1^Ns, 3^rd (la mediana del campione) e 5^ns (Nord^ns) statistiche degli ordini. Quanto segue figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... Mostra U[0, 1] distribuzione:

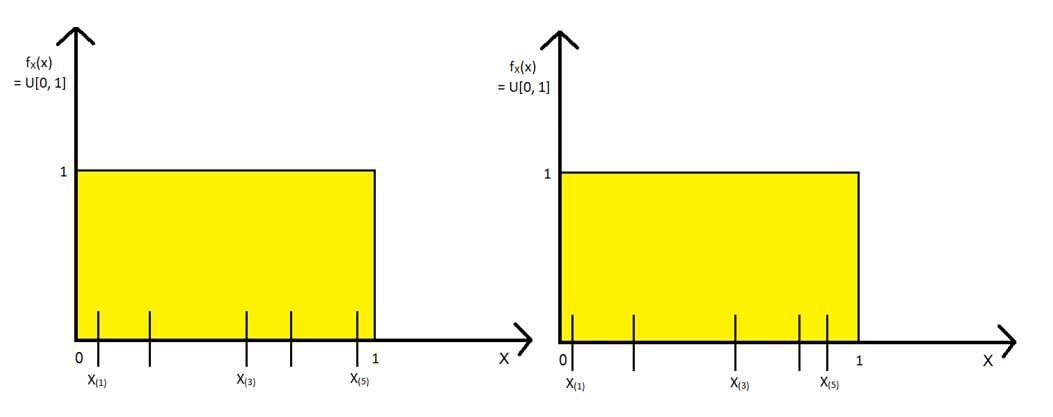
Estrarremo campioni casuali come segue e troveremo il 1^Ns, 3^rd & 5^ns statistica dell'ordine per ogni campione. Di seguito sono riportati due dei campioni:

La distribuzione uniforme standard PDF e CDF sono dati come:

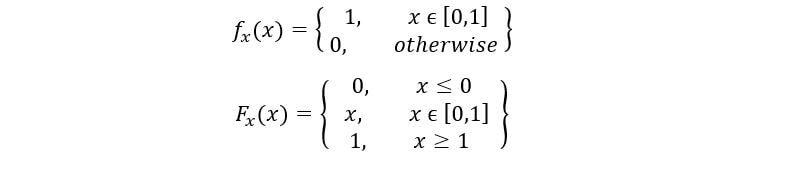
Useremo queste informazioni e calcoleremo X₍₁₎, X₍₃₎ & X₍₅₎ usando le formule che abbiamo derivato. Prenderemo il caso solo quando x è compreso tra 0 e 1 (per altri casi, la statistica dell'ordine è zero poiché PDF è zero).

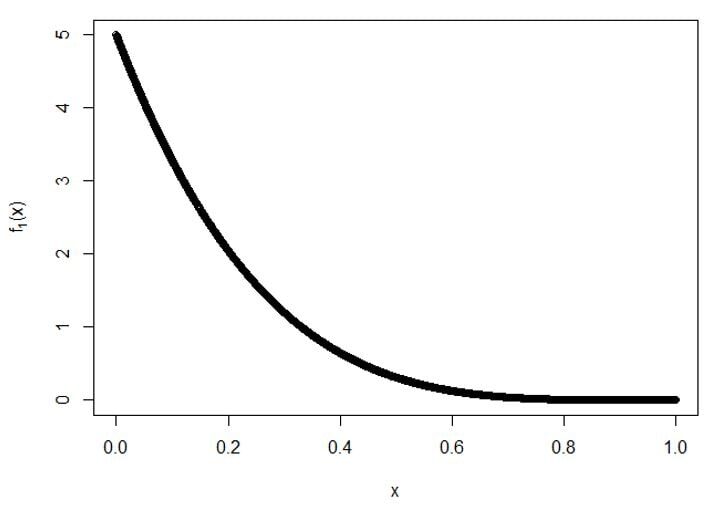
UN) Per 1^Ns statistiche degli ordini:

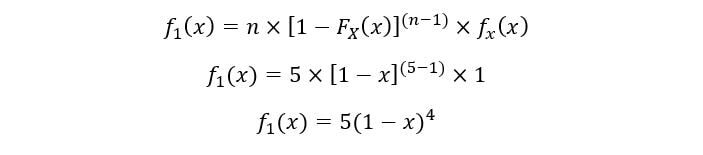
Trama per f₁(X):

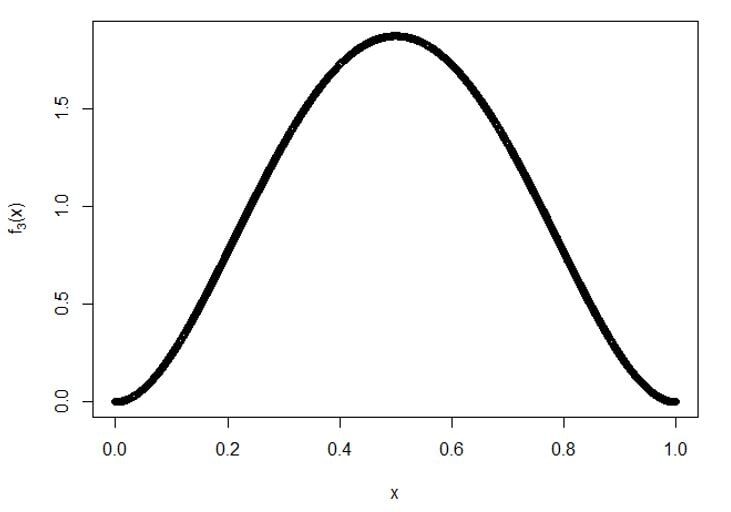
B) Per 3^rd statistiche degli ordini:

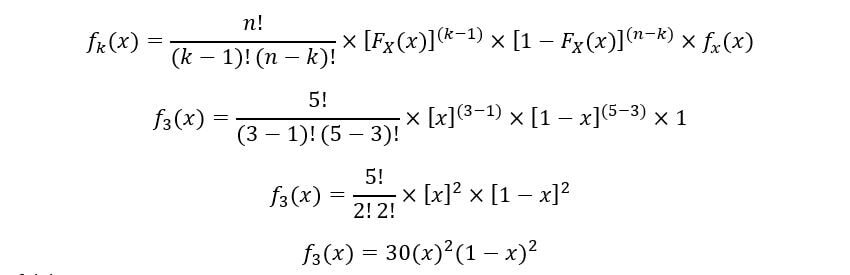
Trama per f₅(X):

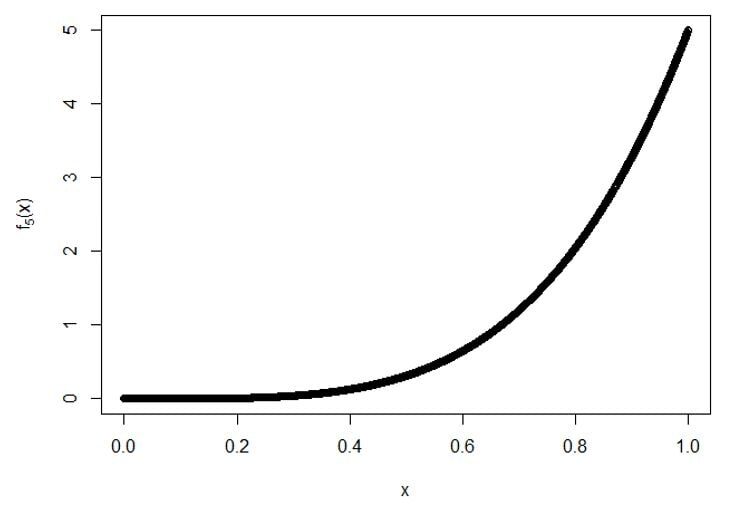
C) Per 5^ns statistiche degli ordini:

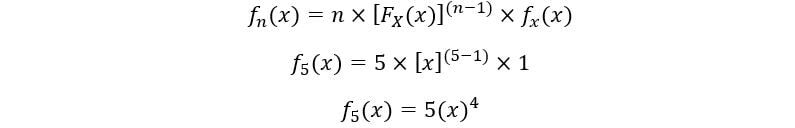
Trama per f₅(X):

conclusione

Perciò, abbiamo approfondito i concetti di statistica dell'ordine. Un'ampia gamma di processi fisici può essere modellata attraverso le statistiche degli ordini, sfruttando le sue proprietà, in particolare le loro distribuzioni.

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato