Big Data

Agrupamento de meias K | Agrupando K-Means com R para Cientistas de Dados

Introdução

Os algoritmos de aprendizado de máquina são classificados em três tipos: aprendizagem supervisionadaO aprendizado supervisionado é uma abordagem de aprendizado de máquina em que um modelo é treinado usando um conjunto de dados rotulados. Cada entrada no conjunto de dados está associada a uma saída conhecida, permitindo que o modelo aprenda a prever resultados para novas entradas. Este método é amplamente utilizado em aplicações como classificação de imagens, Reconhecimento de fala e previsão de tendências, destacando sua importância em..., Aprendizado não supervisionadoO aprendizado não supervisionado é uma técnica de aprendizado de máquina que permite que os modelos identifiquem padrões e estruturas em dados sem rótulos predefinidos. Por meio de algoritmos como k-means e análise de componentes principais, Essa abordagem é usada em uma variedade de aplicações, como segmentação de clientes, detecção de anomalias e compactação de dados. Sua capacidade de revelar informações ocultas o torna uma ferramenta valiosa no... y aprendizaje reforzado. O cluster K-means é uma técnica de aprendizado de máquina não supervisionada. Cuando no se proporciona la variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... de salida o respuesta, este algoritmo é usado para categorizar os dados em diferentes grupos para melhor compreendê-los. Também conhecido como abordagem de aprendizado de máquina baseada em dados, pois agrupa dados com base em padrões ocultos, conhecimento e semelhanças nos dados.

Considere o seguinte diagrama: se você for solicitado a agrupar as pessoas na imagem em diferentes grupos ou grupos e você não souber nada sobre eles, certamente tentará localizar as qualidades, características ou atributos físicos que essas pessoas compartilham. Depois de observar essas pessoas, conclui-se que eles podem ser segregados com base em sua altura e largura; já que você não tem conhecimento prévio sobre essas pessoas. O agrupamento K-means executa um trabalho aproximadamente equivalente. Tente classificar os dados em grupos com base em semelhanças e padrões ocultos. “K” no agrupamento de K-means refere-se ao número de clusters que o algoritmo irá gerar nos dados.

Grupo K-Means: Como funciona?

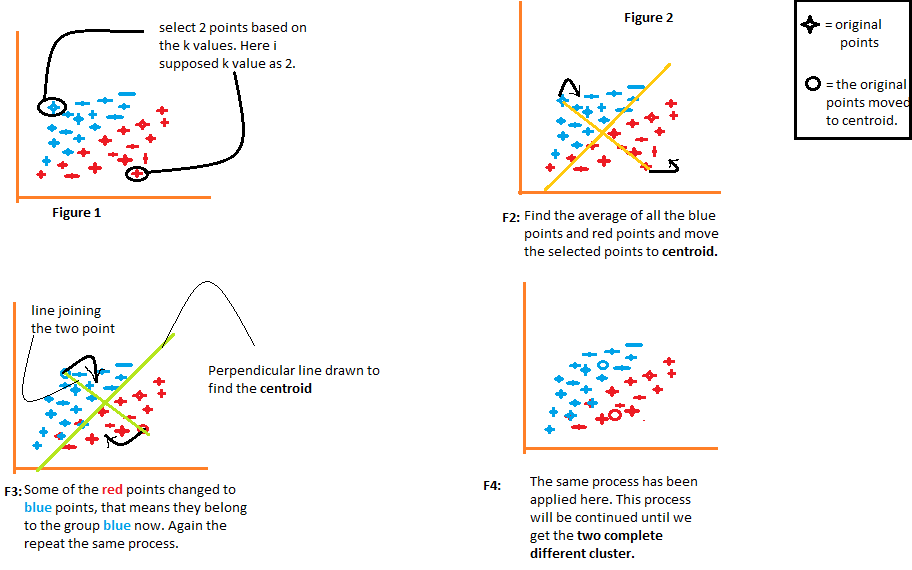
1) O algoritmo escolhe arbitrariamente o número k de centróides, como se indica en la figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.... 1 do diagrama a seguir. Onde k é o número de clusters que o algoritmo criaria. Digamos que queremos que o algoritmo crie dois grupos a partir dos dados, então vamos definir o valor de k para 2.

2) Em seguida, agrupe os dados em duas partes usando as distâncias calculadas de ambos os centróides., como ilustrado na Figura 2. A distância de cada ponto de ambos os centróides é calculada individualmente e posteriormente será adicionada ao grupo daquele centróide com o qual a distância é calculada. mais curta.

O algoritmo também desenha uma linha unindo os centróides e uma linha perpendicular que tenta agrupar os dados em dois grupos.

3) Uma vez que todos os pontos de dados são agrupados com base em suas distâncias mínimas dos centróides correspondentes, o algoritmo calcula a média de cada grupo. Em seguida, os valores médios e centróides de cada grupo são comparados. Se o valor do centróide for diferente da média, então o centróide é deslocado para o valor médio do grupo. Ambos o centróide “vermelho” como ele “azul” são realocados para a média do grupo na figura 3 do diagrama a seguir.

Agrupe os dados mais uma vez usando esses centróides atualizados. Devido à mudança nas posições dos centróides, alguns pontos de dados agora podem ser deslocados no outro grupo.

4) Novamente, calcula a média e a compara com o centroide dos grupos recém-gerados. Se ambos forem diferentes, o centróide será realocado de volta para a média do grupo. Este processo de cálculo da média e comparação com o centróide é repetido até que os valores do centróide e da média sejam iguais. (valor do centróide = média do grupo). Este é o ponto em que o algoritmo segmentou os dados em 'K grupos’ (2 neste caso).

Como descobrir qual é o valor ideal de k?

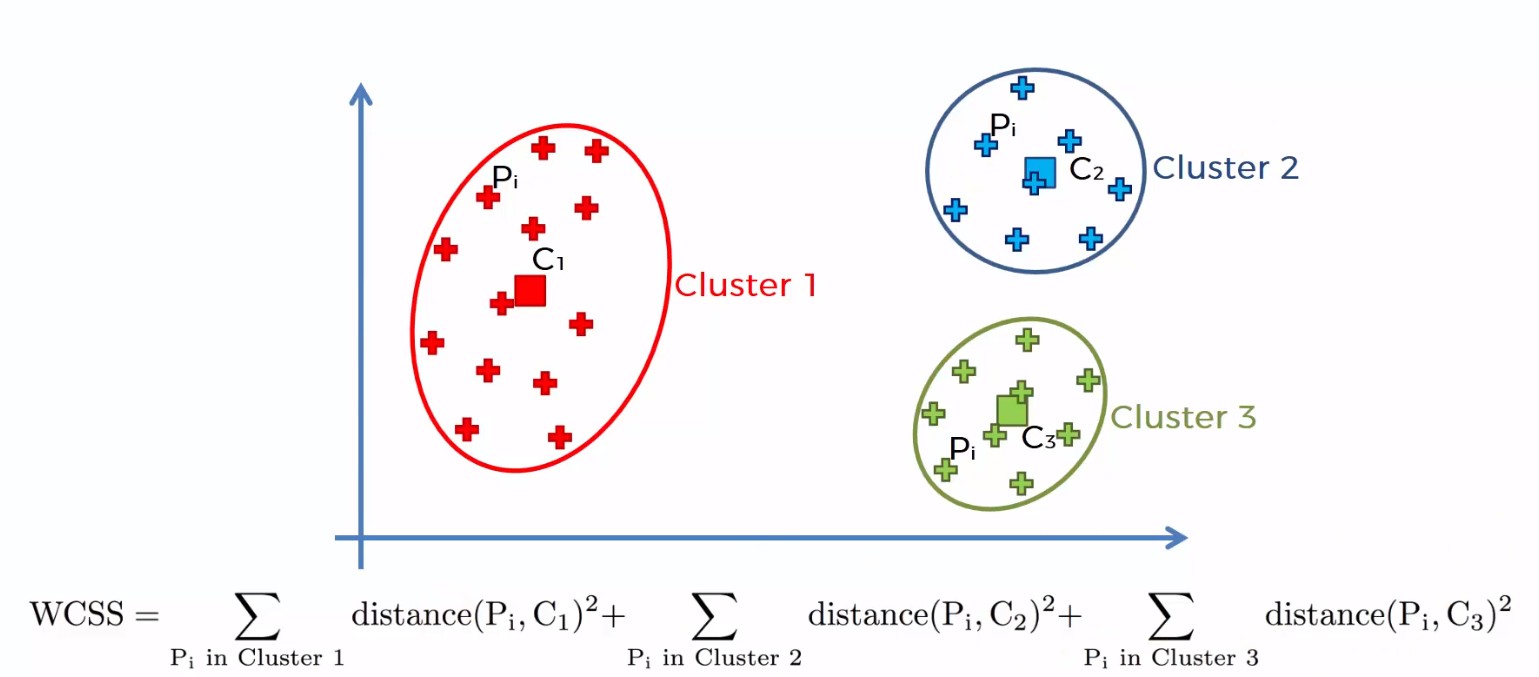
A primeira etapa é fornecer um valor para k. Cada etapa subsequente executada pelo algoritmo é completamente dependente do valor especificado de k. Este valor de k ajuda o algoritmo a determinar o número de clusters para gerar. Isso enfatiza a importância de fornecer o valor preciso de k. Aqui, um método conhecido como o “método do cotovelo” para determinar o valor correto de k. Este é um gráfico de ‘Número de clusters K’ contra “Total dentro da soma do quadrado”. Valores discretos de k são plotados no eixo x, enquanto as somas dos quadrados dos grupos são plotadas no eixo y.

A soma das distâncias quadradas entre os pontos individuais e o centróide em cada grupo, seguido pela soma das distâncias quadradas para todos os clusters, É chamado de "Soma dos quadrados dentro do cluster". Você será capaz de entender isso com a ajuda das seguintes etapas.

1) Calcule a distância entre o centroide e cada ponto do grupo, quadrado e, em seguida, adicione as distâncias ao quadrado para todos os pontos do grupo.

2) Calcule a soma das distâncias quadradas dos grupos restantes da mesma maneira.

3) Finalmente, some todas as somas dos grupos para obter o valor da "Soma do quadrado dentro do grupo" conforme mostrado na figura a seguir.

Src: https://images.app.goo.gl/cVZUiomiGGqKK7SV8

o “total dentro da soma do quadrado” comienza a disminuir a mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que aumenta el valor de k. O gráfico entre o número de clusters e o total dentro da soma dos quadrados é mostrado na figura a seguir. O número ideal de clusters, ou o valor correto de k, é o ponto em que o valor começa a diminuir lentamente; isso é conhecido como o “ponta do cotovelo”, e o ponto de cotovelo no gráfico a seguir é k = 4. o “Método do cotovelo” é nomeado pela semelhança do gráfico com o cotovelo, e o ponto ideal para “k” é a ponta do cotovelo .

Vantagens do agrupamento k-means

1) Os dados marcados não são obrigatórios. Uma vez que muitos dados do mundo real não são rotulados, como resultado, são frequentemente usados em uma variedade de declarações de problemas do mundo real.

2) É fácil de implementar.

3) Pode lidar com grandes quantidades de dados.

4) Quando os dados são grandes, trabalhe mais rápido do que o agrupamento hierárquico (para k pequeninos).

Desvantagens do agrupamento K-means

1) O valor de K deve ser selecionado manualmente usando o “método do cotovelo”.

2) A presença de outliers teria um impacto adverso no agrupamento. Como resultado, outliers devem ser removidos antes de usar o agrupamento k-means.

3) Os grupos não se cruzam; um ponto só pode pertencer a um grupo de cada vez. Como resultado da falta de sobreposição, certos pontos são colocados em grupos errados.

K-significa agrupamento com R

Vamos importar as seguintes bibliotecas para o nosso trabalho.

biblioteca (intercalação)
biblioteca (ggplot2)
biblioteca (dplyr)

Vamos trabalhar com os dados da íris, contendo três classes: “Iris-sedoso”, “Iris-versicolor” e “Iris-virginica”.

dados <- read.csv (& quot; iris.csv & quot;, cabeçalho = T)

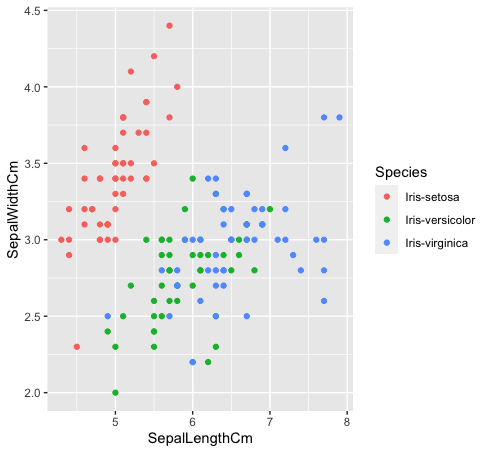
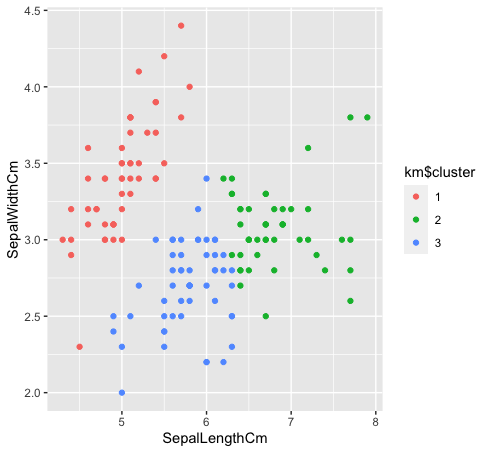
Vamos ver como essas três classes estão relacionadas entre si. As espécies “Iris-versicolor” (verde) e “Iris-verginica” (azul) não são linearmente separáveis. Como você pode ver no gráfico abaixo, eles se misturam.

dados%>% ggplot (aes (SepalLengthCm, SepalWidthCm, cor = Espécie)) +
geom_point ()

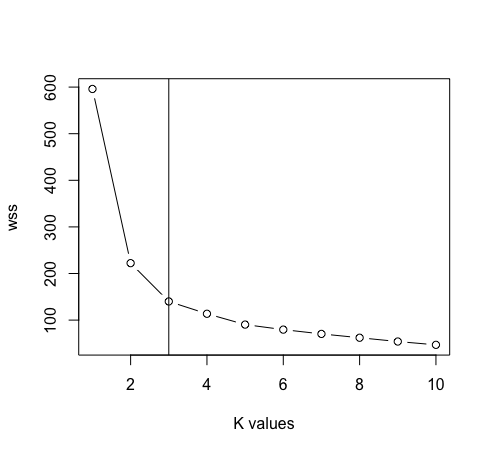
Depois de remover a coluna de espécies dos dados. Agora vamos usar o gráfico do método do cotovelo entre “Soma dos quadrados dentro do cluster” e “Valores K” para determinar o valor apropriado de k. K = 3 é o melhor valor para k neste caso (Observação: existem 3 classes nos dados originais da íris, o que garante a precisão do valor de k).

dados <- dados[, -5]
máximo <- 10
scal <- escala (dados)
wss <- vivamente (1: máximo, Função (k) {kmeans (scal, k, nstart = 50, iter.max = 15) $ tot.withinss})
enredo (1: max, wss, tipo = “b”, xlab = “valores k”)
abline (v = 3)

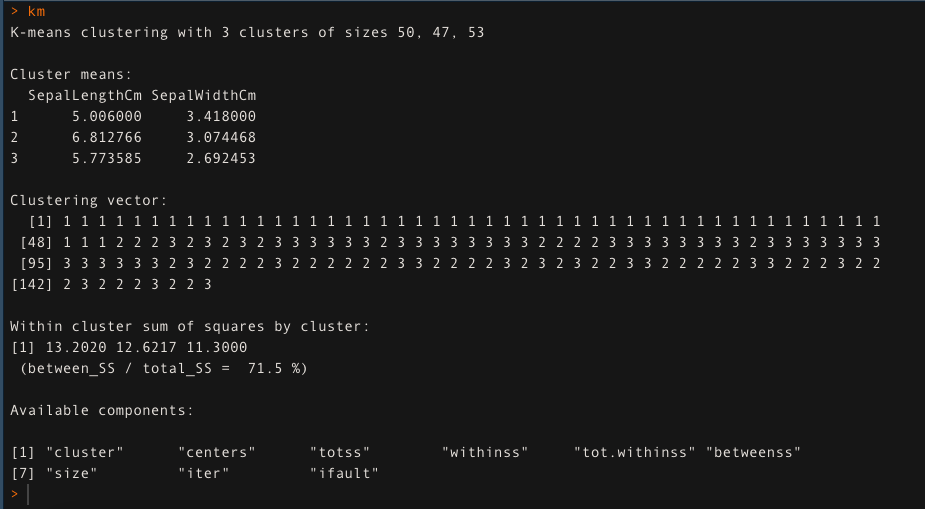
Para k = 3, aplique el algoritmo de agrupamentoo "agrupamento" É um conceito que se refere à organização de elementos ou indivíduos em grupos com características ou objetivos comuns. Este processo é usado em várias disciplinas, incluindo psicologia, Educação e biologia, para facilitar a análise e compreensão de comportamentos ou fenômenos. No campo educacional, por exemplo, O agrupamento pode melhorar a interação e o aprendizado entre os alunos, incentivando o trabalho.. de K-medias. A abordagem de agrupamento K-means explica o 71,5% da variabilidade dos dados neste caso.

km <- kmedias (dados[,1:2], k = 3, iter.max = 50)
km

17950screenshot202021-05-2620at207-08-1220pm-5465633

Vamos ver como as três classes são agrupadas por agrupamento de k-médias. O agrupamento K-means não criará clusters sobrepostos, como todos sabemos. Desde a espécie “verde” e “azul” não são linearmente separáveis nos dados originais, o agrupamento de k-médias não pode capturá-lo porque tem grupos reduzidos.