Algoritmo KNN | Qual é o algoritmo KNN?

Visão geral:

Este artigo da KNN é para:

· Entenda a representação e previsão do algoritmo K mais próximo (KNN).

· Entenda como escolher a métrica de valor k e distância.

· Métodos de preparação de dados necessários e Prós e contras do algoritmo KNN.

· Implementação de pseudocódigo e Python.

Introdução:

K El algoritmo del vecino más cercano se incluye en la categoría de aprendizagem supervisionadaO aprendizado supervisionado é uma abordagem de aprendizado de máquina em que um modelo é treinado usando um conjunto de dados rotulados. Cada entrada no conjunto de dados está associada a uma saída conhecida, permitindo que o modelo aprenda a prever resultados para novas entradas. Este método é amplamente utilizado em aplicações como classificação de imagens, Reconhecimento de fala e previsão de tendências, destacando sua importância em... y se usa para clasificación (mais comumente) e regressão. É um algoritmo versátil que também é usado para imputar valores perdidos e resamplear conjuntos de dados.. Como o nome sugere (K vizinho mais próximo), considerar K vizinhos mais próximos (Os pontos de dados) para prever a classe ou o valor contínuo para o novo ponto de dados.

Aprender o algoritmo é:

1. Aprendizado baseado em instâncias: aquí no aprendemos ponderaciones de los datos de TreinamentoO treinamento é um processo sistemático projetado para melhorar as habilidades, Conhecimento ou habilidades físicas. É aplicado em várias áreas, como esporte, Educação e desenvolvimento profissional. Um programa de treinamento eficaz inclui planejamento de metas, prática regular e avaliação do progresso. A adaptação às necessidades individuais e a motivação são fatores-chave para alcançar resultados bem-sucedidos e sustentáveis em qualquer disciplina.... para predecir la salida (como em algoritmos baseados em modelos), em vez disso, usamos instâncias de treinamento completos para prever a saída de dados invisíveis.

2. Aprendizado preguiçoso: o modelo não é aprendido usando dados de treinamento antes e o processo de aprendizagem é adiado para um momento em que a previsão é solicitada na nova instância.

3. Não paramétrico: Na KNN, não há forma predefinida da função de mapeamento.

Como funciona a KNN??

1. Princípio:

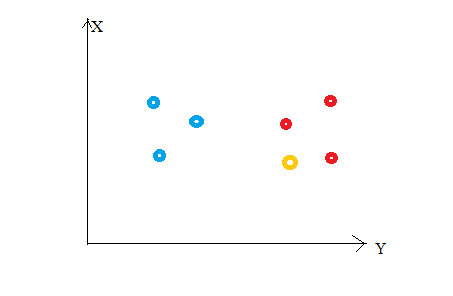
   Considere la siguiente figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas..... Digamos que traçamos pontos de dados do nosso conjunto de treinamento em um espaço de características bidimensionais.. Como mostrado, temos um total de 6 Os pontos de dados (3 vermelho e 3 Azul). Os pontos de dados vermelhos pertencem à classe 1’ e os pontos de dados azuis pertencem à 'classe2'. e o ponto de dados amarelo em um espaço de características representa o novo ponto para o qual prever uma classe. Obviamente, dizemos que pertence a 'classe1’ (pontos vermelhos)

   Por que?

   Porque seus vizinhos mais próximos pertencem a essa classe!!

   

   sim, este é o princípio por trás K Vizinhos Vizinhos. Aqui, os vizinhos mais próximos são aqueles pontos de dados que têm uma distância mínima no espaço de recurso do nosso novo ponto de dados. E K é o número de pontos de dados que consideramos em nossa implementação do algoritmo. Portanto, a métrica de distância e o valor K são duas considerações importantes ao usar o algoritmo KNN. A distância euclidiana é a métrica de distância mais popular. Você também pode usar a distância Hamming, a distância de manhattan, a distância de Minkowski de acordo com suas necessidades. Para prever a classe / valor contínuo para um novo ponto de dados, considera todos os pontos de dados no conjunto de dados de treinamento. Encontre os vizinhos mais próximos (Os pontos de dados) 'K’ dos novos pontos de dados no espaço de recursos e seus rótulos de classe ou valores contínuos.

   Mais tarde:

   Para classificação: um rótulo de classe atribuído à maioria dos K's mais próximos no conjunto de dados de treinamento é considerado uma classe prevista para o novo ponto de dados.

   Para regressão: la media o medianaA mediana é uma medida estatística que representa o valor central de um conjunto de dados ordenados. Para calculá-lo, Os dados são organizados do menor para o maior e o número no meio é identificado. Se houver um número par de observações, Os dois valores principais são calculados em média. Este indicador é especialmente útil em distribuições assimétricas, uma vez que não é afetado por valores extremos.... de los valores continuos asignados a K vecinos más cercanos del conjunto de datos de entrenamiento es un valor continuo predicho para nuestro nuevo punto de datos

2. Representação do modelo
   

   Aqui, não aprendemos pesos e armazená-los, mas todo o conjunto de dados de treinamento é armazenado na memória. Portanto, a representação do modelo para KNN é o conjunto de dados completo de treinamento.

Como escolher o valor de K?

K é um parâmetro crucial no algoritmo KNN. Algumas sugestões para escolher K Value são:

1. Usando curvas de erro: a figura a seguir mostra as curvas de erro para diferentes valores K para os dados de treinamento e teste.

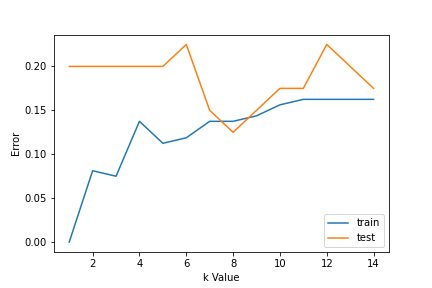
A baixos valores K, há oversetting de dados / alta variância. Portanto, o erro de teste é alto e o erro do trem é baixo. E K = 1 nos dados do trem, o erro é sempre zero, porque o vizinho mais próximo a esse ponto é que o próprio ponto. Portanto, embora o erro de treinamento seja baixo, o erro de teste é alto com valores K mais baixos. Isso é chamado de ajuste excessivo.. UMA mediro "medir" É um conceito fundamental em várias disciplinas, que se refere ao processo de quantificação de características ou magnitudes de objetos, Fenômenos ou situações. Na matemática, Usado para determinar comprimentos, Áreas e volumes, enquanto nas ciências sociais pode se referir à avaliação de variáveis qualitativas e quantitativas. A precisão da medição é crucial para obter resultados confiáveis e válidos em qualquer pesquisa ou aplicação prática.... que aumentamos el valor de K, reduz erro de teste.

Mas depois de um certo valor de K, viés é introduzido / incompatibilidade e erro de teste aumenta. Então, podemos dizer que inicialmente o erro dos dados de teste é alto (devido à variância), então ele desce e estabiliza e com um aumento adicional no valor de K, novamente aumenta (devido ao viés). o valor de k quando o erro de teste estabiliza e é baixo é considerado o valor ideal para k. Da curva de erro anterior, podemos escolher K = 8 para a implementação do nosso algoritmo KNN.

2. O que mais, conhecimento de domínio é muito útil para escolher o valor K.

3. O valor de K deve ser estranho quando se considera a classificação binária (duas classes).

Preparação de dados necessária:

1. Escala de dados: para localizar o ponto de dados no espaço de recursos multidimensionais, seria útil se todos os recursos estão na mesma escala. Portanto, a padronizaçãoA padronização é um processo fundamental em várias disciplinas, que busca estabelecer padrões e critérios uniformes para melhorar a qualidade e a eficiência. Em contextos como engenharia, Educação e administração, A padronização facilita a comparação, Interoperabilidade e compreensão mútua. Ao implementar normas, a coesão é promovida e os recursos são otimizados, que contribui para o desenvolvimento sustentável e a melhoria contínua dos processos.... o estandarización de los datos ayudará.

2. Redução de dimensionalidade: KNN pode não funcionar bem se houver muitos recursos. Portanto, técnicas de redução de dimensionalidade, como seleção de recursos e análise de componentes principais podem ser implementadas.

3. Tratamento de valor ausente: se os recursos M estão faltando dados de um recurso para um exemplo específico no conjunto de treinamento, então não podemos localizar ou calcular a distância a partir desse ponto. Portanto, é necessário excluir essa linha ou imputação.

Implementação Python:

Implementação do algoritmo K vizinho mais próximo usando a biblioteca de aprendizado de scikit do Python:

Paso 1: obter e preparar dados

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier 
from sklearn import metrics

Depois de carregar bibliotecas importantes, criamos nossos dados usando sklearn.datasets com 200 amostras, 8 características e 2 aulas. Mais tarde, dados são divididos no trem (80%) e dados de teste (20%) e escala usando o StandardScaler.

X,Y=make_classification(n_samples= 200.n_features=8.n_informative=8.n_redundant=0.n_repeated=0.n_classes=2.random_state=14)
X_train, X_test, y_train, y_test= train_test_split(X, E, test_size= 0.2.random_state=32)
sc= StandardScaler()
sc.fit(X_train)
X_train= sc.transform(X_train)
sc.fit(X_test)
X_test= sc.transform(X_test)
Forma X

(200, 8)

Paso 2: Encontre o valor de K

Para escolher o valor K, usamos curvas de erro e valor K com variância ideal, e o erro de viés é escolhido como o valor K para fins de previsão. Com a curva de erro plotada abaixo, escolhemos K = 7 para previsão

erro1= []
erro2= []
para k em alcance(1,15):
    knn= KNeighborsClassifier(n_neighbors=k)
    knn.fit(X_train,y_train)
    y_pred1= knn.predict(X_train)
    erro1.append(np.mean(y_train!= y_pred1))
    y_pred2= knn.predict(X_test)
    erro2.append(np.mean(y_test!= y_pred2))
# plt.figure(figsize(10,5))
plt.plot(faixa(1,15),erro1,rótulo="Comboio")
plt.plot(faixa(1,15),erro2,rótulo="teste")
plt.xlabel('k Valor')
plt.ylabel('Erro')
plt.legend()

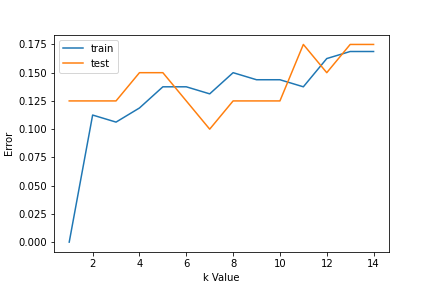
Paso 3: Predizer:

En el paso 2, nós escolhemos que o valor de K é 7. Agora nós substituímos esse valor e o obter a pontuação de precisão = 0,9 para dados de teste.

knn= KNeighborsClassifier(n_neighbors=7)
knn.fit(X_train,y_train)
y_pred= knn.predict(X_test)
metrics.accuracy_score(y_test,y_pred)

0.9

Pseudocódigo para K vizinho mais próximo (classificação):

Relacionado