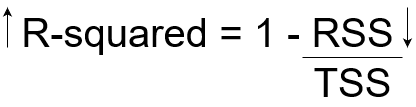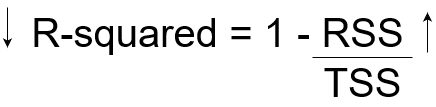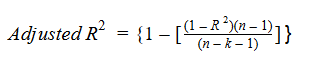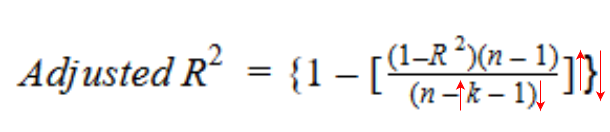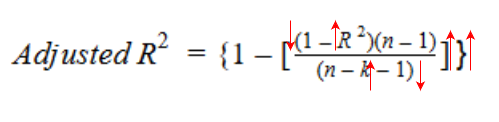Visão geral
- Entenda o conceito de R ao quadrado e R ao quadrado ajustado
- Aprenda as principais diferenças entre R-quadrado e R-quadrado ajustado
Introdução
Quando comecei minha jornada na ciência de dados, o primeiro algoritmo que explorei foi a regressão linear. Depois de entender os conceitos de regressão linear e como o algoritmo funciona, Eu estava realmente animado para usá-lo e fazer previsões sobre uma declaração de problema. Tenho certeza que a maioria de vocês teria feito o mesmo. Mas uma vez que previmos os valores, que segue?
Depois vem a parte complicada. Uma vez que construímos nosso modelo, o próximo passo foi avaliar seu desempenho. Escusado será dizer que a tarefa de avaliação do modelo é fundamental e destaca as deficiências do nosso modelo.. Escolha o mais adequado Avaliação métrica é uma tarefa crucial. E encontrei duas métricas importantes: R-quadrado e R-quadrado ajustado além do MAE / MSE / RMSE. Qual é a diferença entre esses dois? qual devo usar?
R ao quadrado e R ao quadrado ajustado são duas dessas métricas de avaliação que podem parecer confusas para qualquer aspirante a cientista de dados inicialmente.. Uma vez que ambos são extremamente importantes na avaliação de problemas de regressão, vamos entendê-los e compará-los em profundidade. Ambos tem seus prós e contras, que discutiremos em detalhes neste artigo.
Observação: Para entender R-quadrado e R-quadrado ajustado, você deve ter uma boa compreensão da regressão linear. Confira nosso curso gratuito –
Tabela de conteúdo
- Soma de quadrados residual
- Entendendo a estatística R ao quadrado
- Problemas com a estatística R ao quadrado
- Estatística R-quadrado ajustada
Soma de quadrados residual
Para entender os conceitos com clareza, vamos resolver um problema de regressão simples. Aqui, estamos tentando prever as 'notas obtidas’ com base na quantidade de 'tempo gasto estudando'. a clima gasto estudando será nosso variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... Independente e ele marcas registradas realizado no teste é nosso dependente o variável de destino.
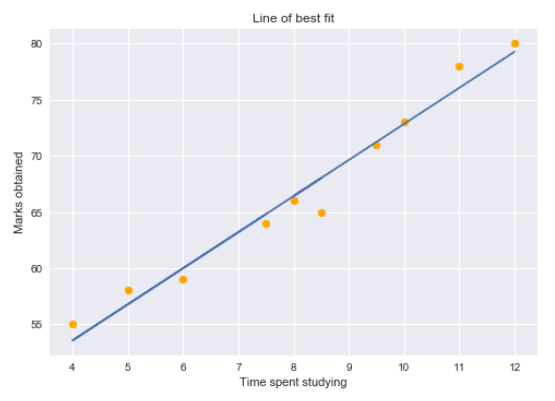
Podemos traçar um gráfico de regressão simples para visualizar esses dados.
Os pontos amarelos representam os pontos de dados e a linha azul é nossa linha de regressão prevista.. Como você pode ver, nosso modelo de regressão não prevê perfeitamente todos os pontos de dados. Então, como avaliamos as previsões da linha de regressão usando os dados? Nós vamos, poderíamos começar determinando os valores residuais para os pontos de dados.
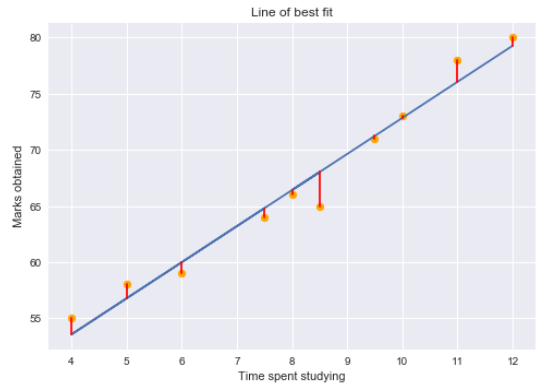
Residual para um ponto nos dados é a diferença entre o valor real e o valor previsto pelo nosso modelo de regressão linear.
Gráficos residuais nos dizem se o modelo de regressão é adequado para os dados ou não. Na realidade, é uma suposição do modelo de regressão que não há tendência nas parcelas residuais. Estudar detalhadamente os pressupostos da regressão linear, sugiro passar esta grande artetítulo!
Usando valores residuais, podemos determinar a soma dos quadrados dos resíduos também conhecido como Soma de quadrados residual ou RSS.
Quanto menor o valor RSS, melhor as previsões do modelo. Ou podemos dizer que uma linha de regressão é uma linha de melhor ajuste se minimizar o valor de RSS. Mas há uma falha nisso: RSS é uma estatística de variante de escala. Como RSS é a soma da diferença quadrática entre o valor real e o valor previsto, o valor depende da escala da variável de destino.
Exemplo:
Considere que sua variável de destino é a receita gerada pela venda de um produto. Os resíduos dependeriam da escala desse objetivo. Se a escala de renda for levada em “centenas de rúpias” (quer dizer, o objetivo seria 1, 2, 3, etc.), então poderíamos obter um feed RSS de cerca de 0,54 (hipoteticamente falando).
Mas se a variável de renda-alvo for levada em consideração “rúpias” (quer dizer, o objetivo seria 100, 200, 300, etc.), então poderíamos obter um RSS maior como 5400. Embora os dados não mudem, O valor do RSS varia. de acordo com a escala de destino. Isso torna difícil julgar o que pode ser um bom valor RSS..
Então, podemos chegar a uma estatística melhor que seja invariável em escala? É aqui que o R-quadrado entra em cena.
Entendendo a estatística R-quadrado
A estatística R ao quadrado ou coeficiente de determinação é uma estatística invariante de escala que fornece a proporção de variação na variável alvo explicada pelo modelo de regressão linear.
Isso pode parecer um pouco complicado, então deixe-me dividi-lo aqui. Para determinar a proporção alvo de variação explicada pelo modelo, Devemos primeiro determinar o seguinte:
-
soma total dos quadrados
A variação total da variável alvo é a soma dos quadrados da diferença entre os valores reais e sua média.
TSS ou soma total de quadrados dá a variação total em Y. Podemos ver que é muito semelhante à variância de Y. Enquanto a variância é a média das somas quadradas da diferença entre os valores reais e os pontos de dados, TSS é o total das somas ao quadrado.
Agora que sabemos a variação total na variável de destino, Como determinamos a proporção dessa variação explicada pelo nosso modelo?? Voltamos ao RSS.
-
Soma de quadrados residual
Como discutimos antes, RSS nos dá o quadrado total da distância dos pontos reais da linha de regressão. Mas se focarmos em um único resíduo, podemos dizer que é a distância que não é capturada pela linha de regressão. Portanto, RSS como um todo nos dá a variação na variável de destino que é não explicado pelo nosso modelo.
-
Calcular R-quadrado
Agora, se TSS nos dá a variação total em Y, e RSS nos dá a variação em Y não explicada por X, então TSS-RSS nos dá a variação em Y que é explicada pelo nosso modelo! Podemos simplesmente dividir esse valor por TSS para obter a proporção de variação em Y explicada pelo modelo. e este nosso Estatística R-quadrado!
R-quadrado = (TSS-RSS) / SST
= Variação explicada / Variação Total
= 1 – variação inexplicável / Variação Total
Então, R ao quadrado fornece o grau de variabilidade na variável alvo que é explicada pelo modelo ou pelas variáveis independentes. Se este valor for 0,7, significa que as variáveis independentes explicam a 70% da variação na variável de destino.
O valor de R ao quadrado está sempre entre 0 e 1. Um valor de R quadrado mais alto indica uma maior quantidade de variabilidade explicada pelo nosso modelo e vice-versa..
Se tivéssemos um valor RSS muito baixo, significaria que a linha de regressão estava muito próxima dos pontos reais. Isso significa que as variáveis independentes explicam a maior parte da variação na variável alvo.. Em tal caso, teríamos um valor R-quadrado muito alto.
Pelo contrário, se tivéssemos um valor RSS muito alto, significaria que a linha de regressão estaria muito longe dos pontos reais. Portanto, as variáveis independentes não explicam a maior parte da variação na variável alvo. Isso nos daria um valor de R-quadrado muito baixo.
Então, isso explica porque o valor de R ao quadrado nos dá a mudança na variável alvo dada pela mudança nas variáveis independentes.
Problemas com a estatística R ao quadrado
A estatística R ao quadrado não é perfeita. De fato, sofre de uma grande falha. Seu valor nunca diminui, não importa quantas variáveis adicionemos ao nosso modelo de regressão.. Quer dizer, mesmo se adicionarmos variáveis redundantes aos dados, o valor de R ao quadrado não diminui. Ele permanece o mesmo ou aumenta com a adição de novas variáveis independentes.. Isso claramente não faz sentido porque algumas das variáveis independentes podem não ser úteis para determinar a variável de destino. O R-quadrado ajustado resolve esse problema.
Estatística R-quadrado ajustada
O R-quadrado ajustado leva em consideração o número de variáveis independentes usadas para prever a variável alvo. Ao fazer isso, podemos determinar se adicionar novas variáveis ao modelo realmente aumenta o ajuste do modelo.
Vamos dar uma olhada na fórmula R-quadrado ajustada para entender melhor como ela funciona.
Aqui,
- Norte representa o número de pontos de dados em nosso conjunto de dados
- k representa o número de variáveis independentes, e
- R representa os valores de R-quadrado determinados pelo modelo.
Então, se R-quadrado não aumenta significativamente com a adição de uma nova variável independente, então o valor ajustado do R-quadrado na verdade diminuirá.
Por outro lado, se ao adicionar a nova variável independente vemos um aumento significativo no valor de R ao quadrado, então o valor ajustado de R ao quadrado também aumentará.
Podemos ver a diferença entre os valores R-quadrado e R-quadrado ajustado se adicionarmos uma variável independente aleatória ao nosso modelo.
Como você pode ver, adicionar uma variável independente aleatória não ajudou a explicar a variação na variável alvo. Nosso valor R-quadrado permanece o mesmo. Portanto, nos dá uma falsa indicação de que essa variável pode ser útil para prever a saída. Porém, o valor ajustado de R quadrado diminuiu, o que indicou que essa nova variável não está realmente capturando a tendência na variável de destino.
Claramente, é melhor usar o R-quadrado ajustado quando houver várias variáveis no modelo de regressão. Isso nos permitiria comparar modelos com diferentes números de variáveis independentes..
Notas finais
Neste artigo, Analisamos o que é a estatística R ao quadrado e onde ela falha. Também damos uma olhada no R quadrado ajustado.
Com sorte, isso deu a ele uma melhor compreensão das coisas. Agora você pode determinar com prudência quais variáveis independentes são úteis para prever o resultado do seu problema de regressão..
Para saber mais sobre outras métricas de avaliação, Sugiro verificar os seguintes ótimos recursos: