Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
Clustering é uma técnica de aprendizado de máquina não supervisionada. É o processo de dividir o conjunto de dados em grupos nos quais os membros do mesmo grupo têm características semelhantes. Os algoritmos de clustering mais amplamente usados são clustering K-means, agrupamento hierárquico, agrupamento baseado em densidade, agrupamento baseado em modelo, etc. Neste artigo, vamos a discutir el agrupamentoo "agrupamento" É um conceito que se refere à organização de elementos ou indivíduos em grupos com características ou objetivos comuns. Este processo é usado em várias disciplinas, incluindo psicologia, Educação e biologia, para facilitar a análise e compreensão de comportamentos ou fenômenos. No campo educacional, por exemplo, O agrupamento pode melhorar a interação e o aprendizado entre os alunos, incentivando o trabalho.. de K-Means en detalle.
Agrupamento de meias K
Es el algoritmo de Aprendizado não supervisionadoO aprendizado não supervisionado é uma técnica de aprendizado de máquina que permite que os modelos identifiquem padrões e estruturas em dados sem rótulos predefinidos. Por meio de algoritmos como k-means e análise de componentes principais, Essa abordagem é usada em uma variedade de aplicações, como segmentação de clientes, detecção de anomalias e compactação de dados. Sua capacidade de revelar informações ocultas o torna uma ferramenta valiosa no... de tipo iterativo más simple y de uso común. Nisto, nós inicializamos aleatoriamente o K número de centróides nos dados (o número de k é encontrado usando o Cotovelo método a ser discutido posteriormente neste artigo) e iterar esses centróides até que nenhuma mudança ocorra na posição do centróide. Vamos repassar as etapas envolvidas em K significa agrupar para um melhor entendimento..
1) Selecione o número de clusters para o conjunto de dados (K)
2) Selecione o número K do centróide
3) Ao calcular a distância euclidiana ou distância de Manhattan, atribuir pontos para centróide mais próximo, criando assim K grupos
4) Agora encontre o centróide original em cada grupo
5) Reatribua todo o ponto de dados com base neste novo centróide, então repita o passo 4 até que a posição do centróide não mude.
Encontrar o número ideal de clusters é uma parte importante deste algoritmo. Um método comumente usado para encontrar o valor ideal de K é Método do cotovelo.
Método do cotovelo
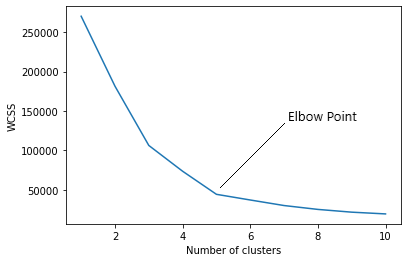
No método do cotovelo, na verdade, estamos variando o número de clusters (K) a partir de 1 uma 10. Para cada valor de K, estamos calculando WCSS (Soma do quadrado dentro do cluster). WCSS é a soma da distância quadrada entre cada ponto e o centróide em um grupo. Quando representamos graficamente o WCSS com o valor K, o gráfico parece um côvado. Conforme o número de clusters aumenta, o valor WCSS começará a diminuir. O valor WCSS é maior quando K = 1. Quando analisamos o gráfico, podemos ver que o gráfico mudará rapidamente em um ponto e, portanto, irá criar uma forma de cotovelo. Deste ponto, o gráfico começa a se mover quase paralelo ao eixo X. O valor K correspondente a este ponto é o valor K ideal ou um número ideal de clusters.
Agora vamos implementar o clustering K-Means usando Python.
Implementação
Em primeiro lugar, temos que importar bibliotecas essenciais.
importar numpy como np import matplotlib.pyplot as plt importar pandas como pd importar sklearn
Agora vamos importar o conjunto de dados e separar os recursos importantes.
dataset = pd.read_csv('Mall_Customers.csv') X = dataset.iloc[:, [3, 4]].valores
Temos que encontrar o valor ideal de K para agrupar os dados. Agora estamos usando o método do cotovelo para encontrar o valor ideal de K.
de sklearn.cluster import KMeans wcss = [] para eu no alcance(1, 11): kmeans = KMeans(n_clusters = i, init ="k-means ++", random_state = 42) kmeans.fit(X) wcss.append(kmeans.inertia_)
O argumento “iniciar” é o método para inicializar o centróide. Calculamos o valor WCSS para cada valor K. Agora temos que plotar o WCSS com o valor K
plt.plot(faixa(1, 11), wcss) plt.xlabel('Número de clusters') plt.ylabel('WCSS') plt.show(
O gráfico será-
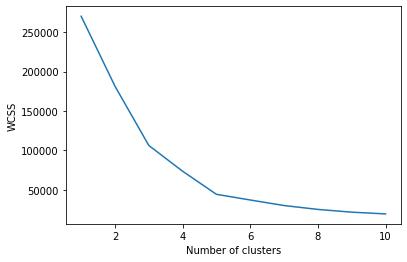
O ponto onde a forma do cotovelo é criada é 5, quer dizer, nosso valor K ou um número ideal de clusters é 5. Agora vamos treinar o modelo no conjunto de dados com vários clusters 5.
kmeans = KMeans(n_clusters = 5, init = "k-means ++", random_state = 42) y_kmeans = kmeans.fit_predict(X)
y_kmeans será:
variedade([3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0,
3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 1,
3, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 2, 1, 2, 4, 2, 4, 2,
1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2])plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c ="vermelho", rótulo ="Cluster1") plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c ="azul", rótulo ="Cluster2") plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c ="verde", rótulo ="Cluster3) plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c = "tolet', rótulo ="Cluster4") plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c ="amarelo", rótulo ="Cluster5") plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c ="Preto", rótulo ="Centroids") plt.xlabel('Rendimento anual (k $)') plt.ylabel('Pontuação de gastos (1-100)') plt.legend() plt.show()
Gráfico:
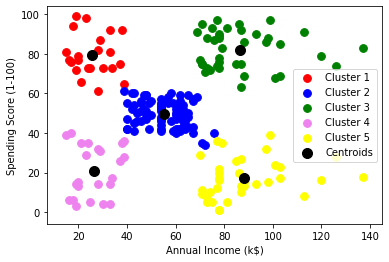
Como você pode ver lá 5 grupos no total que são exibidos em cores diferentes e o centroide de cada grupo é exibido em preto.
Código completo
# Importando as bibliotecas importar numpy como np import matplotlib.pyplot as plt importar pandas como pd # Importando o conjunto de dados X = dataset.iloc[:, [3, 4]].valores dataset = pd.read_csv('Mall_Customers.csv') de sklearn.cluster import KMeans # Usando o método do cotovelo para encontrar o número ideal de clusters wcss = [] para eu no alcance(1, 11): wcss.append(kmeans.inertia_) kmeans = KMeans(n_clusters = i, init ="k-means ++", random_state = 42) kmeans.fit(X) plt.plot(faixa(1, 11), wcss) plt.xlabel('Número de clusters') y_kmeans = kmeans.fit_predict(X) plt.ylabel('WCSS') plt.show() # Treinamento do modelo K-Means no conjunto de dados kmeans = KMeans(n_clusters = 5, init ="k-means ++", random_state = 42) y_kmeans = kmeans.fit_predict(X) # Visualizando os clusters plt.scatter( X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c ="azul", rótulo ="Cluster2") plt.scatter( X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c ="vermelho", rótulo ="Cluster1") plt.scatter( X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c ="verde", rótulo ="Cluster3") plt.scatter( kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c ="Preto", rótulo ="Centroids") plt.scatter( X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c ="tolet", rótulo ="Cluster4") plt.scatter( X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c ="amarelo", rótulo ="Cluster5") plt.xlabel('Rendimento anual (k $)') plt.ylabel('Pontuação de gastos (1-100)') plt.legend() plt.show()
conclusão
Este é o conceito básico do algoritmo de agrupamento K-means em aprendizado de máquina. Nos próximos artigos, podemos obter mais informações sobre diferentes algoritmos de aprendizado de máquina.
A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.
