Observação: Este artigo foi publicado originalmente em 10 Outubro 2014 e atualizou o 27 marchar 2018.
Visão geral
- Entenda k vizinho mais próximo (KNN): um dos algoritmos de aprendizado de máquina mais populares
- Saiba como o kNN funciona em python
- Escolha o valor correto de k em termos simples
Introdução
Nos quatro anos de minha carreira em ciência de dados, Eu construí mais de 80% de modelos de classificação e apenas um 15-20% de modelos de regressão. Essas proporções podem ser mais ou menos generalizadas em toda a indústria. A razão por trás desse preconceito modelos de classificação é que a maioria dos problemas analíticos envolve tomar uma decisão.
Por exemplo, se um cliente vai ou não queimar, se segmentarmos o cliente X para campanhas digitais, se o cliente é de alto potencial ou não, etc. Essas análises são mais perspicazes e diretamente ligadas a um roteiro de implementação.
Neste artigo, falaremos sobre outro aprendizado de máquina amplamente utilizado. técnica de classificaçãomim chamados K-vizinhos mais próximos (KNN). Nosso foco será principalmente em como o algoritmo funciona e como o parâmetro de entrada afeta a saída. / predição.
Observação: Pessoas que preferem aprender através de vídeos podem aprender o mesmo através do nosso curso gratuito – Algoritmo K-Vizinhos Mais Próximos (KNN) em Python e R. E se você é um iniciante absoluto em ciência de dados e aprendizado de máquina, confira nosso programa Certified BlackBelt:
Tabela de conteúdo
- Quando usamos o algoritmo KNN?
- Como funciona o algoritmo KNN?
- Como escolhemos o fator K?
- Quebrá-lo – Pseudo código de KNN
- Implementação em Python do zero
- Comparando nosso modelo com o scikit-learn
Quando usamos o algoritmo KNN?
KNN pode ser usado para classificação preditiva e problemas de regressão. Porém, mais amplamente utilizado em problemas de classificação na indústria. Para avaliar qualquer técnica, costumamos olhar 3 aspectos importantes:
1. Fácil de interpretar a saída
2. tempo de cálculo
3. poder preditivo
Vamos dar alguns exemplos para colocar o KNN na escala:
Feiras de algoritmos KNN em todos os parametroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto.... de considerações. É comumente usado por sua fácil interpretação e baixo tempo de computação..
Como funciona o algoritmo KNN?
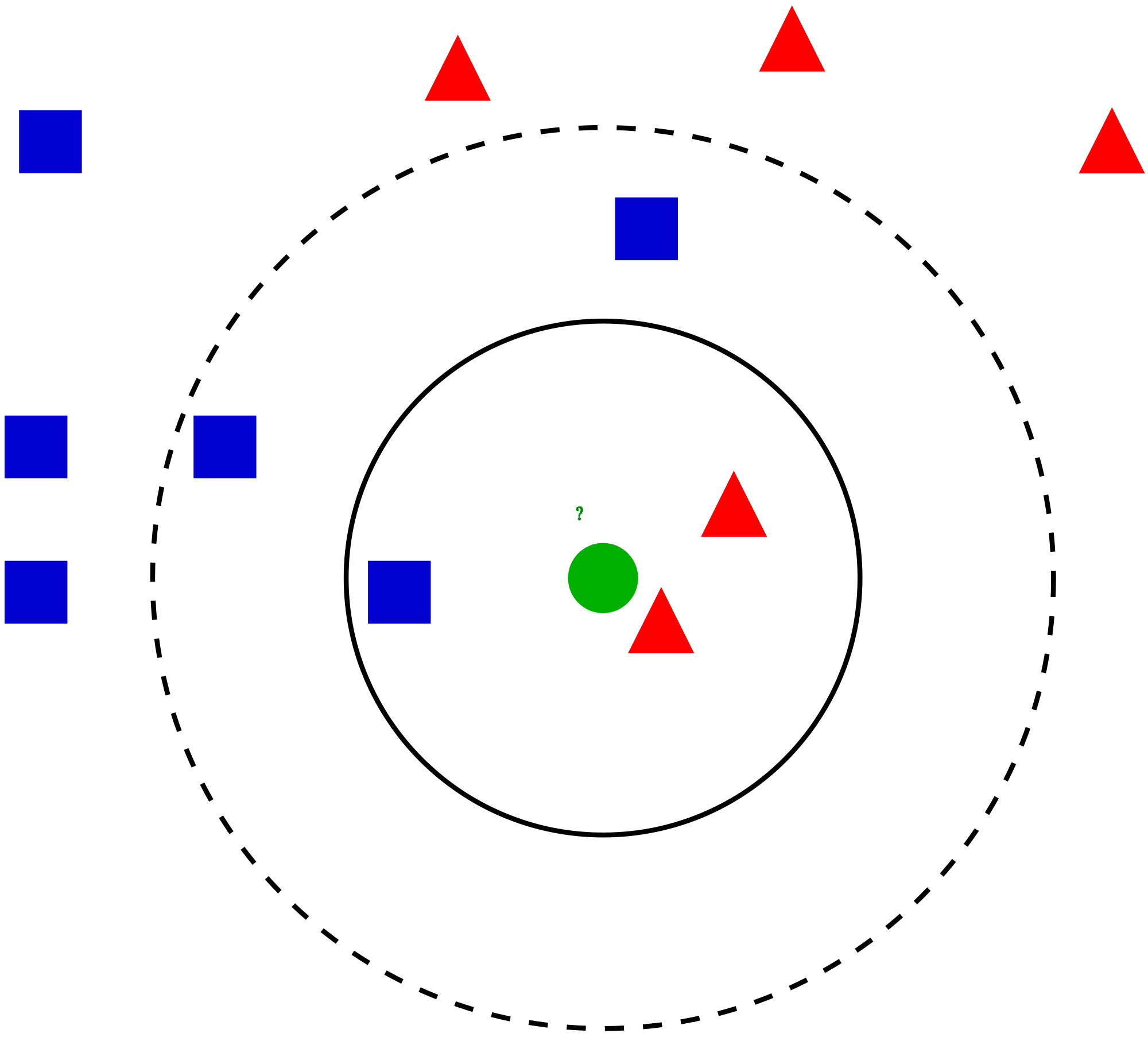
Vamos pegar um caso simples para entender esse algoritmo. Abaixo está uma extensão de círculos vermelhos (RC) e quadrados verdes (GS):
Ele pretende descobrir a classe da estrela azul (BS). BS pode ser RC ou GS e nada mais. O Algoritmo “K” é KNN é o vizinho mais próximo em que queremos votar. Digamos K = 3. Portanto, agora vamos fazer um círculo com BS como centro grande o suficiente para incluir apenas três pontos de dados no plano. Consulte o diagrama a seguir para obter mais detalhes:
Os três pontos mais próximos de BS são todos RC. Por tanto, com um bom nível de confiança, podemos dizer que o BS deve pertencer à classe RC. Aqui, a escolha ficou muito óbvia, pois todos os três votos do vizinho mais próximo foram para RC. A escolha do parâmetro K é muito importante neste algoritmo. A seguir, entenderemos quais são os fatores a considerar para concluir o melhor K.
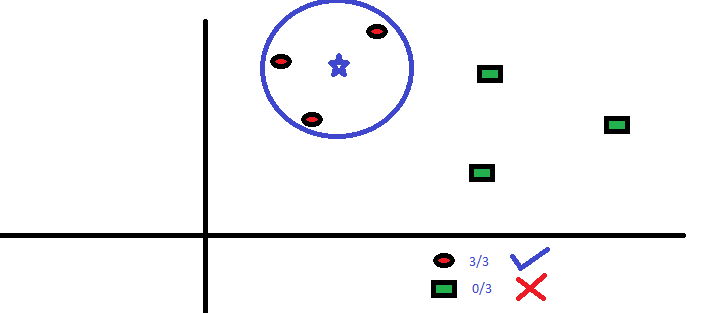
Como escolhemos o fator K?
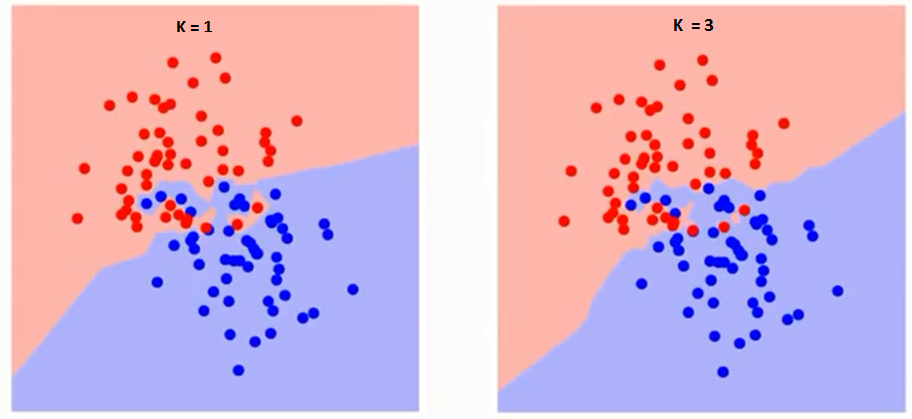
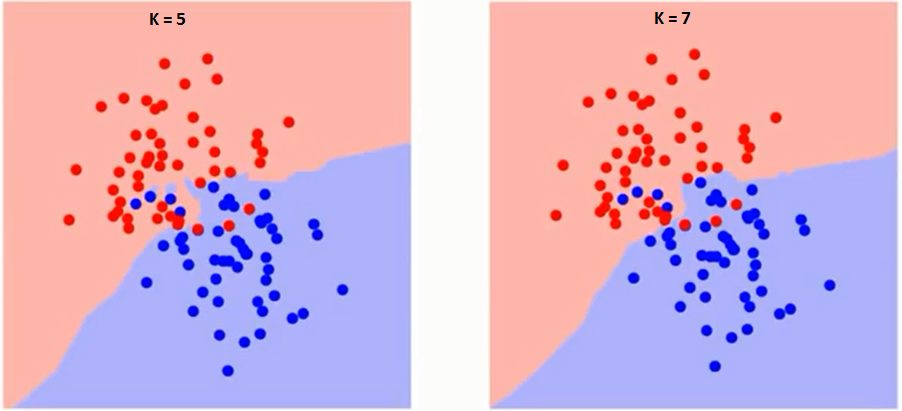
Vamos primeiro tentar entender o que exatamente influencia K no algoritmo. Se olharmos para o último exemplo, desde o 6 Observações de TreinamentoO treinamento é um processo sistemático projetado para melhorar as habilidades, Conhecimento ou habilidades físicas. É aplicado em várias áreas, como esporte, Educação e desenvolvimento profissional. Um programa de treinamento eficaz inclui planejamento de metas, prática regular e avaliação do progresso. A adaptação às necessidades individuais e a motivação são fatores-chave para alcançar resultados bem-sucedidos e sustentáveis em qualquer disciplina.... permanecer constante, com um determinado valor de K podemos definir limites para cada classe. Esses limites separarão RC de GS. Da mesma maneira, Vamos tentar ver o efeito do valor “K” nos limites da classe. A seguir estão os diferentes limites que separam as duas classes com diferentes valores de K.
Se você olhar com atenção, você pode ver que o limite se torna mais suave com o aumento do valor de K. Com K aumentando ao infinito, eventualmente fica todo azul ou todo vermelho, dependendo da maioria. A taxa de erro de treinamento e a taxa de erro de validação são dois parâmetros que precisamos para acessar diferentes valores de K. Abaixo está a curva para a taxa de erro de treinamento com um valor variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... por K:
Como você pode ver, a taxa de erro em K = 1 é sempre zero para a amostra de treinamento. Isso ocorre porque o ponto mais próximo de qualquer ponto de dados de treinamento é ele mesmo, então a previsão é sempre precisa com K = 1. Se a curva de erro de validação tivesse sido semelhante, nossa escolha de K teria sido 1. Abaixo está a curva de erro de validação com um valor variável de K:
Isso esclarece a história. E K = 1, estávamos superajustando os limites. Por tanto, a taxa de erro inicialmente diminui e atinge um mínimo. Após o ponto mínimo, aumenta com o aumento de K. Para obter o valor ótimo de K, você pode separar o treinamento e a validação do conjunto de dados inicial. Agora plote a curva de erro de validação para obter o valor ideal de K. Este valor de K deve ser usado para todas as previsões.
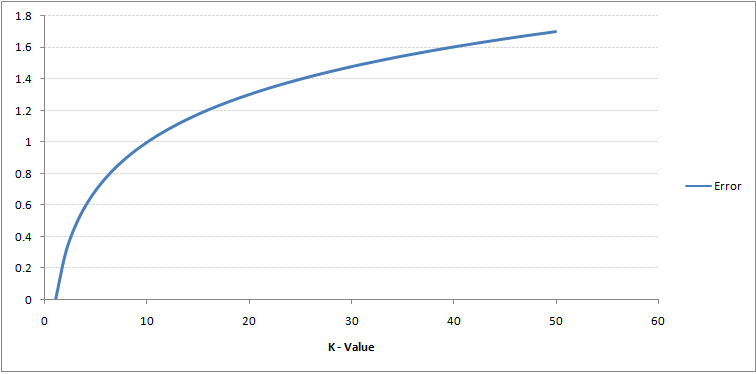
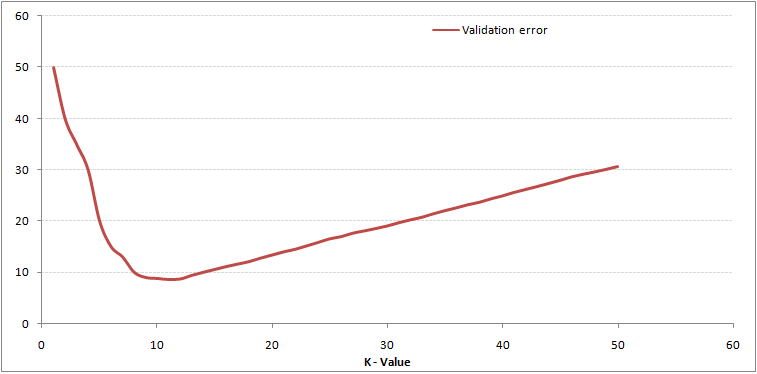
O conteúdo acima pode ser entendido de forma mais intuitiva usando nosso curso gratuito: algoritmo do vizinho mais próximo (KNN) em Python e R
Quebrá-lo – Pseudo código de KNN
Podemos implementar um modelo KNN seguindo as etapas abaixo:
- Carregar dados
- Inicialize o valor de k
- Para obter a classe prevista, repetir de 1 ao número total de pontos de dados de treinamento
- Calcule a distância entre os dados do teste e cada linha de dados de treinamento. Aqui usaremos a distância euclidiana como nossa métrica de distância, como é o método mais popular. As outras métricas que podem ser usadas são Chebyshev, co-seno, etc.
- Classifique as distâncias calculadas em ordem ascendente de acordo com os valores de distância
- Obtenha as primeiras linhas k da matriz ordenada
- Obtenha a classe mais frequente nestas linhas
- Retorna a classe prevista
Implementação em Python do zero
Usaremos o popular conjunto de dados Iris para construir nosso modelo KNN. Você pode baixá-lo de aqui.
Comparando nosso modelo com o scikit-learn
from sklearn.neighbors import KNeighborsClassifier neigh = KNeighborsClassifier(n_neighbors=3) neigh.fit(data.iloc[:,0:4], dados['Nome']) # Predicted class print(neigh.prever(teste)) -> ['Iris-virginica'] # 3 nearest neighbors print(neigh.kneighbors(teste)[1]) -> [[141 139 120]]
Podemos ver que ambos os modelos previram a mesma classe ('Iris-virginica') e os mesmos vizinhos mais próximos ( [141 139 120] ). Portanto, podemos concluir que nosso modelo funciona como esperado.
Implementação de kNN em R
Paso 1: importar os dados
Paso 2: verificar os dados e calcular o resumo dos dados
Produção
#Top observations present in the data SepalLength SepalWidth PetalLength PetalWidth Name 1 5.1 3.5 1.4 0.2 Iris-sedoso 2 4.9 3.0 1.4 0.2 Iris-sedoso 3 4.7 3.2 1.3 0.2 Iris-sedoso 4 4.6 3.1 1.5 0.2 Iris-sedoso 5 5.0 3.6 1.4 0.2 Iris-sedoso 6 5.4 3.9 1.7 0.4 Iris-setosa #Check the dimensions of the data [1] 150 5 #Summarise the data SepalLength SepalWidth PetalLength PetalWidth Name Min. :4.300 Mín.. :2.000 Mín.. :1.000 Mín.. :0.100 Iris-sedoso :50 1St. Qu.:5.100 1St. Qu.:2.800 1St. Qu.:1.600 1St. Qu.:0.300 Iris-versicolor:50 Mediar :5.800 Mediar :3.000 Mediar :4.350 Mediar :1.300 Iris-virginica :50 Quer dizer :5.843 Quer dizer :3.054 Quer dizer :3.759 Quer dizer :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Máx.. :7.900 Máx.. :4.400 Máx.. :6.900 Máx.. :2.500
Paso 3: dividir os dados
Paso 4: Calcule a distância euclidiana
Paso 5: escrever a função para prever kNN
Paso 6: Cálculo do rótulo (Nome) para K = 1
Produção
Para K=1 [1] "Iris-virginica"
Da mesma maneira, pode calcular outros valores de K.
Comparação da nossa função de previsão kNN com a biblioteca “Classe”
Produção
Para K=1 [1] "Iris-virginica"
Podemos ver que ambos os modelos previram a mesma classe ('Iris-virginica').
Notas finais
O algoritmo KNN é um dos algoritmos de classificação mais simples. Mesmo com tanta simplicidade, pode dar resultados altamente competitivos. O algoritmo KNN também pode ser usado para problemas de regressão. A única diferença da metodologia discutida será o uso das médias dos vizinhos mais próximos em vez de votar nos vizinhos mais próximos. KNN pode ser codificado em uma única linha em R. Ainda tenho que explorar como podemos usar o algoritmo KNN no SAS.
O artigo foi útil para você? Você usou alguma outra ferramenta de aprendizado de máquina recentemente? Você planeja usar o KNN em algum dos seus problemas de negócios? Sim é assim, diga-nos como você planeja fazer isso.
