Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
Big Data refere-se a uma combinação de dados estruturados e não estruturados que podem ser medidos em petabytes ou exabytes. Em geral, usamos 3V para caracterizar o 3V de big data, quer dizer, o volume de dados, a variedade de tipos de dados e a velocidade com que são processados.
Essas três características dificultam o tratamento de big data. Portanto, Big data é caro em termos de investimento em uma grande quantidade de armazenamento do servidor, Máquinas de análise sofisticadas e metodologias de mineração de dados. METROQualquer organização acha isso complicado tanto técnica quanto economicamente e, portanto, Você está pensando em como alcançar Resultados semelhantes podem ser alcançados usando muito menos sofisticação.. Portanto, estão tentando transformar big data em small data., consistindo em blocos de dados utilizáveis. La siguiente figura"Figura" é um termo usado em vários contextos, Da arte à anatomia. No campo artístico, refere-se à representação de formas humanas ou animais em esculturas e pinturas. Em anatomia, designa a forma e a estrutura do corpo. O que mais, em matemática, "figura" está relacionado a formas geométricas. Sua versatilidade o torna um conceito fundamental em várias disciplinas.... [1] Mostrar uma comparação.
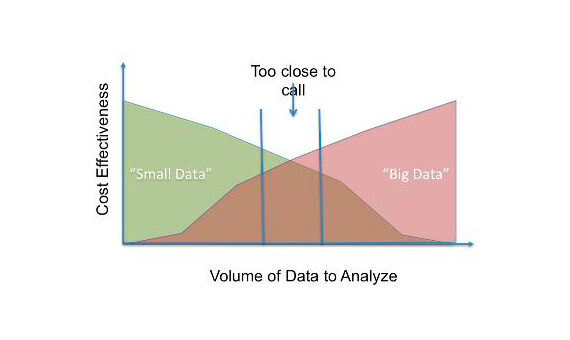
Vamos tentar explorar uma técnica estatística simples, que pode ser usado para criar um pedaço utilizável de dados a partir de big data. A amostra, que é basicamente um subconjunto da população, devem ser seleccionados de modo a representar adequadamente a população. Isso pode ser garantido com o uso de testes estatísticos..
Introdução à amostragem de reservatórios
A ideia-chave por trás da amostragem de reservatórios é criar um "reservatório"’ De um grande oceano de dados. Vamos N’ tamanho da população e 'n’ O tamanho da amostra. Cada elemento da população tem a mesma probabilidade de estar presente na amostra e essa probabilidade é (n / N). Com esta ideia-chave, Precisamos criar uma subamostra. Deve-se notar que quando criamos uma amostra, As distribuições devem ser idênticas não apenas em linhas, mas também em colunas.
Em geral, Focamos apenas nas linhas, Mas também é importante manter a distribuição das colunas. Las columnas son las características de las que aprende el algoritmo de TreinamentoO treinamento é um processo sistemático projetado para melhorar as habilidades, Conhecimento ou habilidades físicas. É aplicado em várias áreas, como esporte, Educação e desenvolvimento profissional. Um programa de treinamento eficaz inclui planejamento de metas, prática regular e avaliação do progresso. A adaptação às necessidades individuais e a motivação são fatores-chave para alcançar resultados bem-sucedidos e sustentáveis em qualquer disciplina..... Portanto, Também temos que realizar testes estatísticos para cada característica para garantir que a distribuição seja idêntica..
O algoritmo é o seguinte: Inicializar o reservatório com o primeiro 'n’ elementos populacionais de tamanho 'N'. Em seguida, leia cada linha do conjunto de dados (eu> n). Em cada iteração, calcule (n / eu). Substituímos os elementos reservatório do seguinte conjunto de 'n’ elementos com probabilidade gradualmente decrescente.
R[eu] = S[eu]
para i = n+1 a N:
j = U ~ [1, eu]
se j <= n:
R[j] = S[eu]
Testes estatísticos
Como eu mencionei antes, Temos de garantir que todas as colunas (caracteristicas) dos reservatórios são distribuídos de forma idêntica à população. Utilizaremos o teste de Kolmogorov-Smirnov para características contínuas e o teste qui-quadrado de Pearson para características categóricas..
O teste de Kolmogorov-Smirnov é usado para verificar se as funções de distribuição cumulativa (CDF) da população e da amostra são as mesmas. Comparamos as CDF da população F_N (x) com a da amostra F_n (x).
𝐹𝑁𝑥
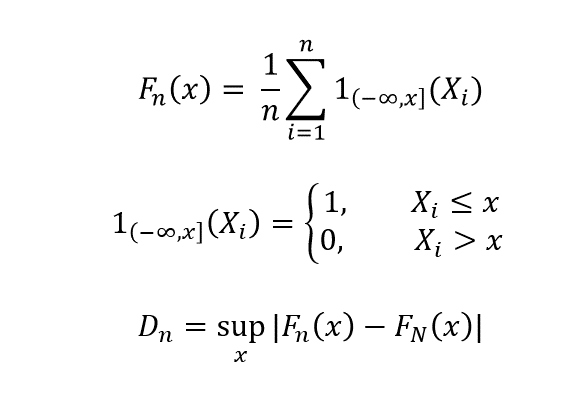
Como n -> N, D_n -> 0, se as distribuições forem idênticas. Esse teste deve ser executado para todas as características do conjunto de dados que são contínuas.
Para características categóricas, podemos realizar o teste do qui-quadrado de Pearson. Deixe-O_i o número de comentários na categoria 'i’ e ne o número de amostras. Vamos E_i a contagem esperada da categoria 'i'. Então E_i = N p_i, onde p_i é a probabilidade de pertencer à categoria 'i'. Em seguida, o valor do qui-quadrado é dado pela seguinte relação::
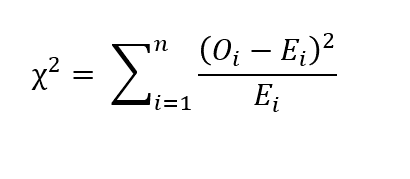
Se qui-quadrado = 0, Isso significa que os valores observados e os valores esperados são os mesmos.. Se o valor de p do teste estatístico for maior que o nível de significância, Dizemos que a amostra é estatisticamente significativa.
Notas finais
A amostragem de reservatório pode ser usada para criar uma parte útil de dados de big data, desde que os dois testes, Kolmogorov-Smirnov e o qui-quadrado de Pearson, são bem-sucedidos. Rumores recentes são, claro, Grande volume de dados. Modelos centralizados como na arquitetura de big data são acompanhados de grandes dificuldades. Descentralizar as coisas e, portanto, Torne o trabalho modular, Temos que criar pequenos pedaços de dados úteis e, em seguida, obter insights significativos a partir deles.. Penso que devem ser envidados mais esforços nesse sentido., Em vez de investir em arquitetura para suportar big data.
Referências
1. https://www.bbvaopenmind.com/en/technology/digital-world/small-data-vs-big-data-back-to-the-basics/






