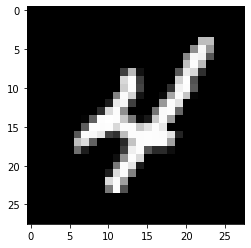Este artigo foi publicado como parte do Data Science Blogathon
Os vários métodos de aprendizado profundo usam dados para treinar algoritmos de rede neural para realizar uma variedade de tarefas de aprendizado de máquina., como a classificação de diferentes classes de objetos. Redes neurais convolucionais são algoritmos de aprendizado profundo muito poderosos para análise de imagens. Este artigo irá explicar como construir, treinar e avaliar redes neurais convolucionais.
Você também aprenderá como melhorar sua capacidade de aprender com os dados e interpretar os resultados do treinamento.. O Deep Learning tem várias aplicações, como processamento de imagem, processamento de linguagem natural, etc. Também é usado em Ciências Médicas, Mídia e entretenimento, Carros Autônomos, etc.
O que é CNN?
CNN é um algoritmo poderoso para processamento de imagem. Esses algoritmos são atualmente os melhores algoritmos que temos para processamento automatizado de imagens.. Muitas empresas usam esses algoritmos para fazer coisas como identificar objetos em uma imagem.
As imagens contêm dados de combinação RGB. Matplotlib pode ser usado para importar uma imagem de um arquivo para a memória. O computador não vê uma imagem, tudo que você vê é uma matriz de números. Imagens coloridas são armazenadas em matrizes tridimensionais. As primeiras duas dimensões correspondem à altura e largura da imagem (o número de pixels). A última dimensão corresponde às cores vermelhas, verde e azul presentes em cada pixel.
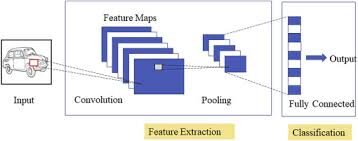
Três camadas da CNN
Redes neurais convolucionais especializadas para aplicações de reconhecimento de imagem e vídeo. CNN é usado principalmente em tarefas de análise de imagem, como reconhecimento de imagem, detecção e segmentação de objetos.
Existem três tipos de camadas em redes neurais convolucionais:
1) Capa convolucional: em uma rede neural típica, cada neurônio de entrada é conectado à próxima camada oculta. E CNN, apenas uma pequena região dos neurônios da camada de entrada se conecta à camada oculta de neurônios.
2) Camada de agrupamento: camada de agrupamento é usada para reduzir a dimensionalidade do mapa de feições. Haverá várias camadas de ativação e agrupamento dentro da camada oculta da CNN.
3) Camada totalmente conectada: Camadas totalmente conectadas formar o último capas na rede. A entrada para o camada totalmente conectada é a saída do agrupamento ou convolução final Capa, que é achatado e, em seguida, introduzido no camada totalmente conectada.
Conjunto de dados MNIST
Neste artigo, vamos trabalhar no reconhecimento de objetos em dados de imagem usando o conjunto de dados MNIST para reconhecimento de dígitos manuscritos.
O conjunto de dados MNIST consiste em imagens de dígitos de uma variedade de documentos digitalizados. Cada imagem é um quadrado de 28 x 28 píxeis. Neste conjunto de dados, se utilizam 60.000 imagens para treinar o modelo e 10.000 fotos para testar o modelo. Existem 10 dígitos (0 uma 9) o 10 classes para prever.
Carregando o conjunto de dados MNIST
Instale a biblioteca TensorFlow e importe o conjunto de dados como um conjunto de dados de treinamento e teste.
Plote a saída amostral da imagem
!pip install tensorflow
from keras.datasets import mnist
import matplotlib.pyplot as plt
(X_train,y_train), (X_test, y_test)= mnist.load_data()
plt.subplot()
plt.imshow(X_train[9], cmap=plt.get_cmap('cinza'))
Produção:
Modelo de aprendizagem profunda com perceptrons multicamadas usando MNIST
Neste modelo, vamos criar um modelo de rede neural simples com uma única camada oculta para o conjunto de dados MNIST para reconhecimento de dígitos manuscritos.
Um perceptron é um modelo de neurônio único que é o bloco de construção das maiores redes neurais. O perceptron multicamadas consiste em três camadas, quer dizer, a camada de entrada, a camada oculta e a camada de saída. A camada oculta não é visível para o mundo exterior. Apenas a camada de entrada e a camada de saída são visíveis. Para todos os modelos DL, os dados devem ser de natureza numérica.
Paso 1: importar bibliotecas-chave
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
Paso 2: remodelar dados
Cada imagem tem um tamanho de 28X28, para o que há 784 píxeis. Então, a camada de saída tem 10 Saídas, a camada oculta tem 784 neurônios ea camada de entrada tem 784 ingressos. Mais tarde, o conjunto de dados torna-se um tipo de dados flutuante.
number_pix=X_train.forma[1]*X_train.shape[2]
X_train=X_train.remodele(X_train.shape[0], number_pix).astype('float32')
X_test=X_test.remodele(X_test.shape[0], number_pix).astype('float32')
Paso 3: normaliza dados
Os modelos NN geralmente requerem dados dimensionados. Neste trecho de código, os dados são normalizados a partir de (0-255) uma (0-1) e a variável alvo é codificada em um único uso para análise suplementar. A variável alvo tem um total de 10 aulas (0-9)
X_train=X_train/255
X_test=X_test/255
y_train= np_utils.to_categorical(y_train)
y_test= np_utils.to_categórico(y_test)
num_classes=y_train.forma[1]
imprimir(num_classes)
Produção:
10
Agora, vamos criar uma função NN_model e compilá-la
Paso 4: definir a função modelo
nn_model def():
modelo=Sequencial()
model.add(Denso(number_pix, input_dim=number_pix, ativação = 'reler'))
mode.add(Denso(num_classes, ativação = 'softmax'))
model.compile(perda ="categorical_crossentropy", otimista="Adão", metrics =['precisão'])
modelo de retorno
Há duas camadas, uma é uma camada oculta com a função de gatilho ReLu e a outra é a camada de saída que usa a função softmax.
Paso 5: execute o modelo
model = nn_model()
model.fit(X_train, y_train, validação_data =(X_test,y_test),épocas = 10, batch_size = 200, verboso = 2)
score = model.evaluate(X_test, y_test, verbose = 0)
imprimir('O erro é: %.2f %% '%(100-pontuação[1]*100))
Produção:
Época 1/10 300/300 - 11s - perda: 0.2778 - precisão: 0.9216 - val_loss: 0.1397 - val_accuracy: 0.9604 Época 2/10 300/300 - 2s - perda: 0.1121 - precisão: 0.9675 - val_loss: 0.0977 - val_accuracy: 0.9692 Época 3/10 300/300 - 2s - perda: 0.0726 - precisão: 0.9790 - val_loss: 0.0750 - val_accuracy: 0.9778 Época 4/10 300/300 - 2s - perda: 0.0513 - precisão: 0.9851 - val_loss: 0.0656 - val_accuracy: 0.9796 Época 5/10 300/300 - 2s - perda: 0.0376 - precisão: 0.9892 - val_loss: 0.0717 - val_accuracy: 0.9773 Época 6/10 300/300 - 2s - perda: 0.0269 - precisão: 0.9928 - val_loss: 0.0637 - val_accuracy: 0.9797 Época 7/10 300/300 - 2s - perda: 0.0208 - precisão: 0.9948 - val_loss: 0.0600 - val_accuracy: 0.9824 Época 8/10 300/300 - 2s - perda: 0.0153 - precisão: 0.9962 - val_loss: 0.0581 - val_accuracy: 0.9815 Época 9/10 300/300 - 2s - perda: 0.0111 - precisão: 0.9976 - val_loss: 0.0631 - val_accuracy: 0.9807 Época 10/10 300/300 - 2s - perda: 0.0082 - precisão: 0.9985 - val_loss: 0.0609 - val_accuracy: 0.9828 O erro é: 1.72%
Nos resultados do modelo, é visível conforme o número de épocas aumenta, melhora a precisão. O erro é de 1,72%, menor é o erro, quanto maior a precisão do modelo.
Modelo de rede neural convolucional usando MNIST
Nesta secção, criaremos modelos CNN simples para MNIST que demonstram camadas convolucionais, agrupamento de camadas e camadas de abandono.
Paso 1: importar todas as bibliotecas necessárias
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
from keras.layers import Dropout
from keras.layers import Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
Paso 2: Configure a semente para reprodutibilidade e carregue os dados MNIST
seed=10
np.random.seed(semente)
(X_train,y_train), (X_test, y_test)= mnist.load_data()
Paso 3: converter dados em valores flutuantes
X_train=X_train.remodele(X_train.shape[0], 1,28,28).astype('float32')
X_test=X_test.remodele(X_test.shape[0], 1,28,28).astype('float32')
Paso 4: normaliza dados
X_train=X_train/255
X_test=X_test/255
y_train= np_utils.to_categorical(y_train)
y_test= np_utils.to_categórico(y_test)
num_classes=y_train.forma[1]
imprimir(num_classes)
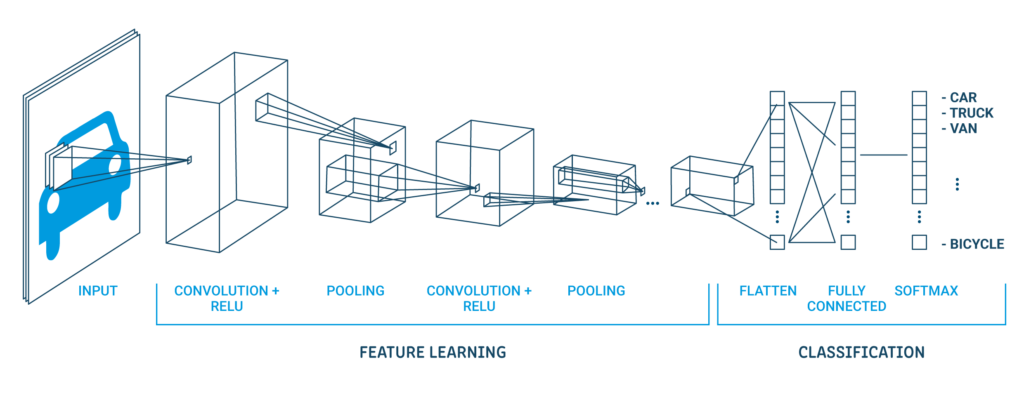
Uma arquitetura clássica da CNN parece abaixo:
| Camada de saída (10 Saídas) |
| Manto oculto (128 neurônios) |
| Camada plana |
| Camada de abandono 20% |
| Camada máxima de agrupamento 2 × 2 |
| Capa convolucional 32 mapas, 5 × 5 |
| Camada visível 1x28x28 |
A primeira camada oculta é uma camada convolucional chamada Convolution2D. Ele tem 32 mapas de características com tamanho 5 × 5 e função de moagem. Esta é a camada de entrada. A seguir está a camada de pool que assume o valor máximo chamado MaxPooling2D. Neste modelo, está configurado como um tamanho de pool de 2 × 2.
A regularização ocorre na camada de abandono. Está configurado para excluir aleatoriamente o 20% neurônios de camada para evitar overfitting. A quinta camada é a camada achatada que converte os dados da matriz 2D em um vetor chamado Achatar. Permite que a saída seja totalmente processada por uma camada padrão totalmente conectada.
A seguir, a camada totalmente conectada é usada com 128 neurônios e a função de ativação do retificador. Finalmente, a camada de saída tem 10 neurônios para 10 classes e uma função de gatilho softmax para gerar previsões do tipo probabilidade para cada classe.
Paso 5: execute o modelo
def cnn_model():
modelo=Sequencial()
model.add(Conv2D(32,5,5, preenchimento = 'mesmo',input_shape =(1,28,28), ativação = 'reler'))
model.add(MaxPooling2D(pool_size =(2,2), preenchimento = 'mesmo'))
model.add(Cair fora(0.2))
model.add(Achatar())
model.add(Denso(128, ativação = 'reler'))
model.add(Denso(num_classes, ativação = 'softmax'))
model.compile(perda ="categorical_crossentropy", otimizador ="Adão", metrics =['precisão'])
modelo de retorno
model = cnn_model()
model.fit(X_train, y_train, validação_data =(X_test,y_test),épocas = 10, batch_size = 200, verboso = 2)
score = model.evaluate(X_test, y_test, verbose = 0)
imprimir('O erro é: %.2f %% '%(100-pontuação[1]*100))
Produção:
Época 1/10 300/300 - 2s - perda: 0.7825 - precisão: 0.7637 - val_loss: 0.3071 - val_accuracy: 0.9069 Época 2/10 300/300 - 1s - perda: 0.3505 - precisão: 0.8908 - val_loss: 0.2192 - val_accuracy: 0.9336 Época 3/10 300/300 - 1s - perda: 0.2768 - precisão: 0.9126 - val_loss: 0.1771 - val_accuracy: 0.9426 Época 4/10 300/300 - 1s - perda: 0.2392 - precisão: 0.9251 - val_loss: 0.1508 - val_accuracy: 0.9537 Época 5/10 300/300 - 1s - perda: 0.2164 - precisão: 0.9325 - val_loss: 0.1423 - val_accuracy: 0.9546 Época 6/10 300/300 - 1s - perda: 0.1997 - precisão: 0.9380 - val_loss: 0.1279 - val_accuracy: 0.9607 Época 7/10 300/300 - 1s - perda: 0.1856 - precisão: 0.9415 - val_loss: 0.1179 - val_accuracy: 0.9632 Época 8/10 300/300 - 1s - perda: 0.1777 - precisão: 0.9433 - val_loss: 0.1119 - val_accuracy: 0.9642 Época 9/10 300/300 - 1s - perda: 0.1689 - precisão: 0.9469 - val_loss: 0.1093 - val_accuracy: 0.9667 Época 10/10 300/300 - 1s - perda: 0.1605 - precisão: 0.9493 - val_loss: 0.1053 - val_accuracy: 0.9659 O erro é: 3.41%
Nos resultados do modelo, é visível conforme o número de épocas aumenta, melhora a precisão. O erro é 3.41%, menor erro maior precisão do modelo.
Espero que tenha gostado de ler e fique à vontade para usar meu código para testá-lo para seus propósitos. O que mais, se houver algum comentário sobre o código ou apenas a postagem do blog, sinta-se à vontade para me contatar em [e-mail protegido]
A mídia mostrada neste artigo de processamento de imagem da CNN não é propriedade da DataPeaker e é usada a critério do autor.
