Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
¿Interesado en análisis predictivo? Luego, investigue la inteligencia artificial, el aprendizaje automático y el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud.... .
Si está en el camino del aprendizaje de la ciencia de datos, definitivamente comprende lo que es el aprendizaje automático. En el mundo digital actual, todo el mundo sabe qué es el aprendizaje automático porque era una tecnología digital de moda en todo el mundo.
Cada paso hacia la adaptación del mundo futuro está liderado por esta tecnología actual, y esta tecnología actual está liderada por científicos de datos como usted y como yo😌.

Aquí solo hablamos del aprendizaje automático, si no sabe qué es, le damos una breve introducción:
Aprendizaje automático es el estudio de los algoritmos de las computadoras, que mejoran automáticamente a través de la experiencia y mediante el uso de datos. su algoritmo construye un modelo basado en los datos que proporcionamos durante la construcción del modelo. Esta es la definición simple de aprendizaje automático, y cuando profundizamos, encontramos que hay una gran cantidad de algoritmos que se utilizan en la construcción de modelos. Generalmente, los algoritmos de aprendizaje automático más utilizados se basan en el tipo de problema, los tipos son básicamente regresión, clasificación, etc… Pero aquí solo hablaremos de algoritmos de regresión.

Hagamos una breve introducción sobre lo que es la regresión. Regresión es el método estadístico en inversiones, finanzas y otras disciplinas que intenta determinar la fuerza y la relación entre las variables independientes y dependientes. Generalmente, las variables independientes son aquellas variables en las que sus valores se utilizan para obtener la salida y las dependientes son aquellas cuyo valor depende de valores independientes. Cuando se habla de algoritmos de regresión, algunos algoritmos de regresión más utilizados se utilizan para entrenar el modelo de aprendizaje automático, como regresión lineal simple, lazo, cresta, etc.
Por lo tanto, hablemos de la regresión lineal múltiple y comprendamos detalladamente en qué se diferencia lo lineal simple de la regresión lineal múltiple.

- Regresión lineal simple vs regresión lineal múltiple
- Conjunto de datos
- Leer conjunto de datos
- Variables independientes y dependientes
- Manejo de variables categóricas
- División de datos
- Aplicando modelo
Regresión lineal simple versus regresión lineal múltiple
Ahora, antes de seguir adelante, analicemos la interacción detrás de la regresión lineal simple, luego tratamos de comparar la regresión lineal simple y múltiple en función de esa intuición que realmente estamos haciendo con nuestro problema de aprendizaje automático.
Regresión lineal simple
Consideramos una regresión lineal simple en cualquier algoritmo de aprendizaje automático usando el ejemplo,
Ahora, suponga que si tomamos un escenario de precio de la vivienda donde nuestro eje x es el tamaño de la casa y el eje y es básicamente el precio de la casa. En esto básicamente, tenemos dos características, la primera es f1 y el segundo es f2, dónde,
f1 se refiere al tamaño de la casa y,
f2 se refiere al precio de la casa
Así que si f1 se convierte en la característica independiente y f2 se convierte en la característica dependiente, generalmente sabemos que siempre que el tamaño de la casa aumenta, el precio también aumenta, supongamos que dibujamos puntos de dispersión al azar, por este punto de dispersión básicamente tratamos de encontrar la línea de mejor ajuste y esta línea de mejor ajuste viene dada por la ecuación :
ecuación: y = A + Bx
Suponer, y ser el precio de la casa y X sea el tamaño de la casa, entonces esta ecuación parece así:
ecuación: precio = A + B (tamaño)
dónde,
A es una intersección y B es una pendiente en esa intersección
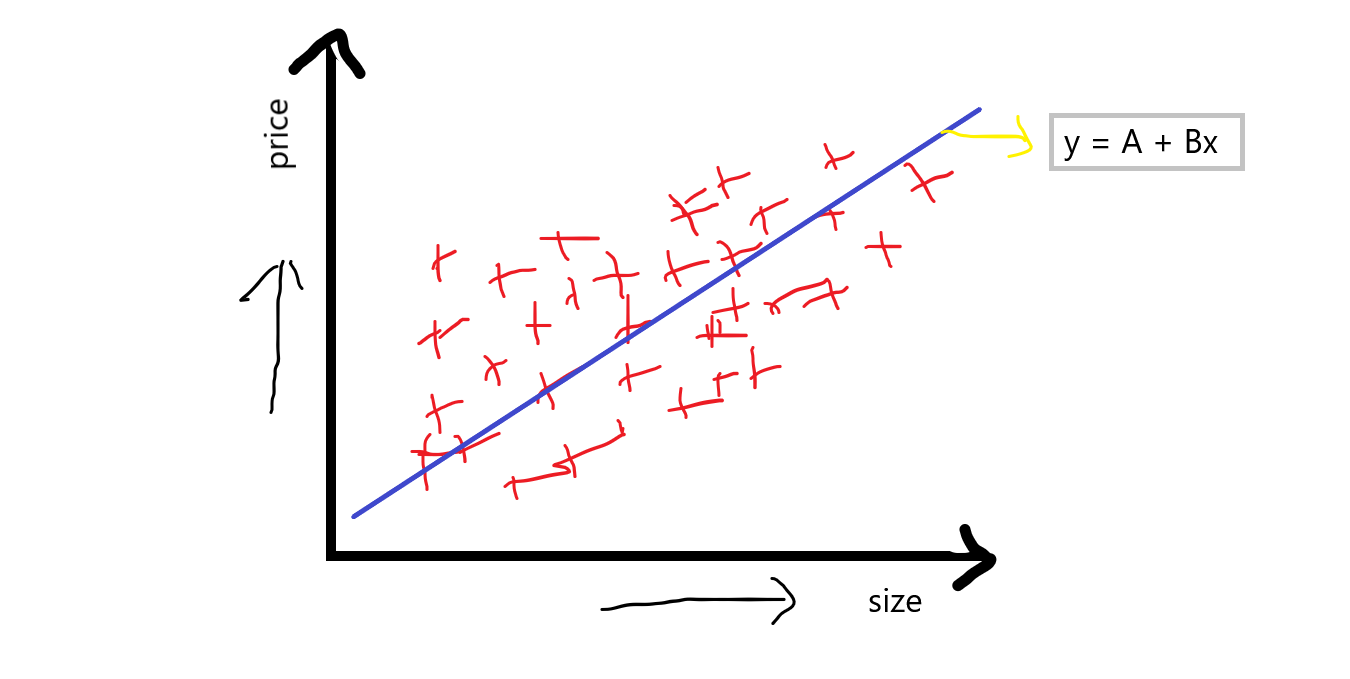
Cuando discutimos esta ecuación, en la cual la intersección básicamente indica cuando el precio de la casa es 0 entonces cuál será el precio base de la casa, y la pendiente o coeficiente indica que con la unidad aumenta de tamaño, entonces lo que será la unidad aumenta en pendiente.
Ahora bien, ¿en qué se diferencia en comparación con la regresión lineal múltiple?
Regresión lineal múltiple
La regresión lineal múltiple básicamente indica que tendremos muchas características como f1, f2, f3, f4, y nuestra función de salida f5. Si tomamos el mismo ejemplo que discutimos anteriormente, suponga:
f1 es el tamaño de la casa.
f2 Son malas habitaciones en la casa.
f3 es la localidad de la casa.
f4 es el estado de la casa y,
f5 es nuestra característica de salida que es el precio de la casa.
Ahora, puede ver que múltiples características independientes también tienen un gran impacto en el precio de la casa, el precio puede variar de una característica a otra. Cuando hablamos de regresión lineal múltiple, entonces la ecuación de regresión lineal simple y = A + Bx se convierte en algo como:
ecuación: y = A + B1X1+ B2X2+ B3X3+ B4X4
«Si tenemos una función dependiente y varias funciones independientes, básicamente lo llamamos regresión lineal múltiple. «
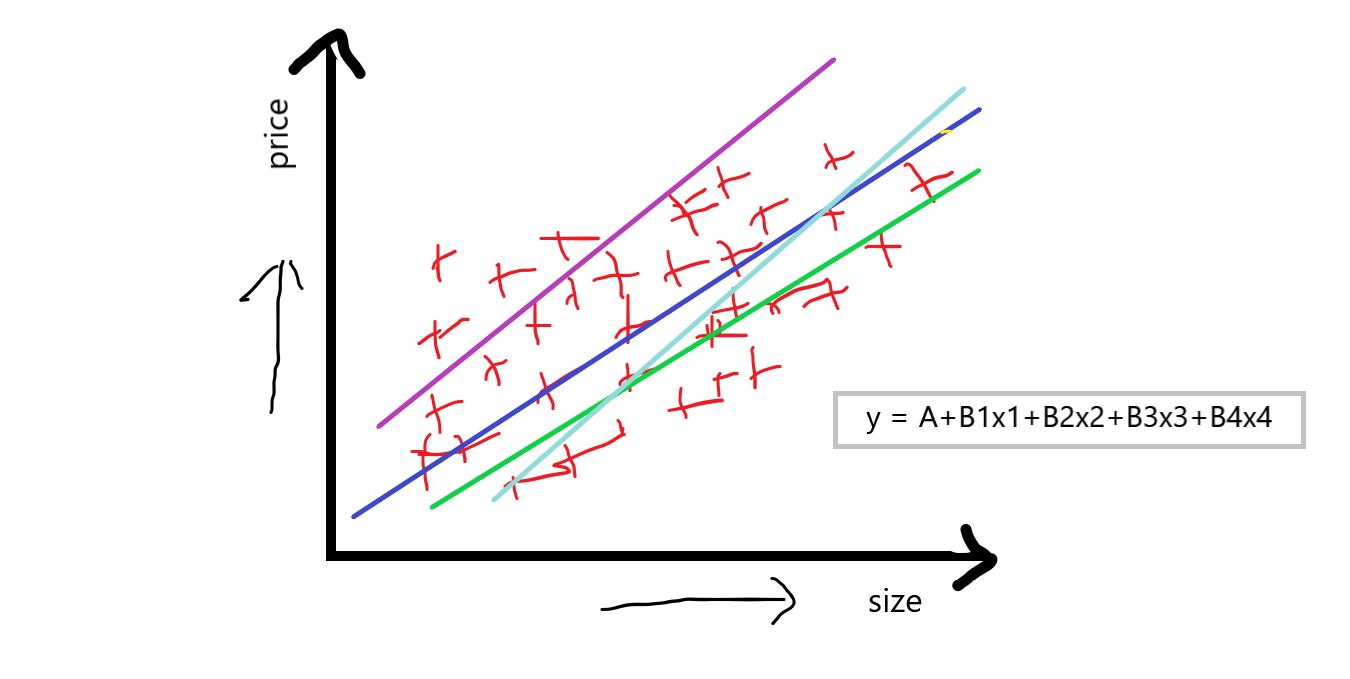
Ahora, nuestro objetivo al utilizar la regresión lineal múltiple es que tenemos que calcular A que es una intersección, y B1 B2 B3 B4 que son las pendientes o coeficientes referentes a esta característica independiente, que básicamente indica que si aumentamos el valor de X1 por 1 unidad entonces B1 dice que cuánto valor afectará en el precio de la casa, y esto fue similar con respecto a otros B2 B3 B4
Entonces, esta es una pequeña descripción teórica de la regresión lineal múltiple. Ahora usaremos la biblioteca de regresión lineal scikit learn para resolver el problema de regresión lineal múltiple.
Conjunto de datos
Ahora, aplicamos regresión lineal múltiple en el 50_startups conjunto de datos, puede hacer clic en aquí para descargar el conjunto de datos.
Leer conjunto de datos
La mayor parte del conjunto de datos está en un archivo CSV, para leer este archivo usamos la biblioteca pandas:
df = pd.read_csv('50_Startups.csv')
df
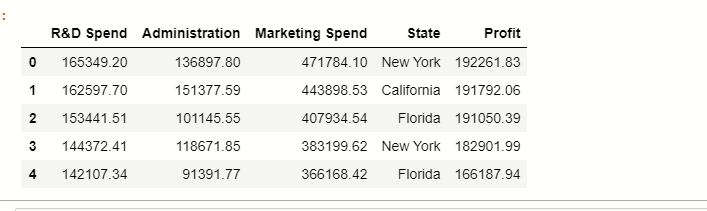
Aquí puede ver que hay 5 columnas en el conjunto de datos donde el estado almacena los puntos de datos categóricos y el resto son características numéricas.
Ahora, tenemos que clasificar características independientes y dependientes:
Variables independientes y dependientes
Hay un total de 5 características en el conjunto de datos, en las que básicamente las ganancias son nuestra característica dependiente, y el resto de ellas son nuestras características independientes:
#separate the other attributes from the predicting attribute
x = df.drop('Profit',axis=1)
#separte the predicting attribute into Y for model training
y = ['profit']
Manejo de variables categóricas
En nuestro conjunto de datos, hay una columna categórica Estado, tenemos que manejar estos valores categóricos presentes dentro de esta columna para eso usaremos pandas get_dummies () función:
# manejar variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... categórica
estados = pd.get_dummies (x, drop_first = True)
# eliminando columna adicional
x = x.drop (‘Estado’, eje = 1)
# concatenación de variables independientes y nueva variable cateórica.
x = pd.concat ([x,states], eje = 1)
X
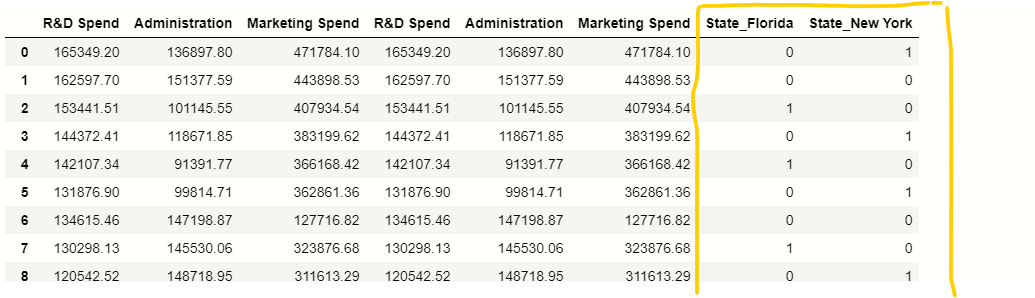
División de datos
Ahora, tenemos que dividir los datos en partes de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y prueba para las que usamos scikit-learn train_test_split () función.
# importing train_test_split from sklearn from sklearn.model_selection import train_test_split # splitting the data x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state = 42)
Aplicando modelo
Ahora, aplicamos el modelo de regresión lineal a nuestros datos de entrenamiento, en primer lugar, tenemos que importar la regresión lineal de la biblioteca scikit-learn, no hay otra biblioteca para implementar la regresión lineal múltiple, lo hacemos solo con regresión lineal.
# importing module from sklearn.linear_model import LinearRegression # creating an object of LinearRegression class LR = LinearRegression() # fitting the training data LR.fit(x_train,y_train)
finalmente, si ejecutamos esto, entonces nuestro modelo estará listo, ahora tenemos datos de x_test, usamos estos datos para la predicción de lucro.
y_prediction = LR.predict(x_test) y_prediction

Ahora, tenemos que comparar los valores de y_prediction con los valores originales porque tenemos que calcular la precisión de nuestro modelo, que fue implementado por un concepto llamado r2_score. discutamos brevemente sobre r2_score:
r2_score: –
Es una función dentro de sklearn. módulo de métricas, donde el valor de r2_score varía entre 0 y 100 por ciento, podemos decir que está estrechamente relacionado con la MSE.
r2 se calcula básicamente mediante la fórmula que se indica a continuación:
fórmula: r2 = 1 – (SSres / SSsignificar )
ahora, cuando digo SSres es decir, es la suma de los residuos y SSsignificar se refiere a la suma de medias.
dónde,
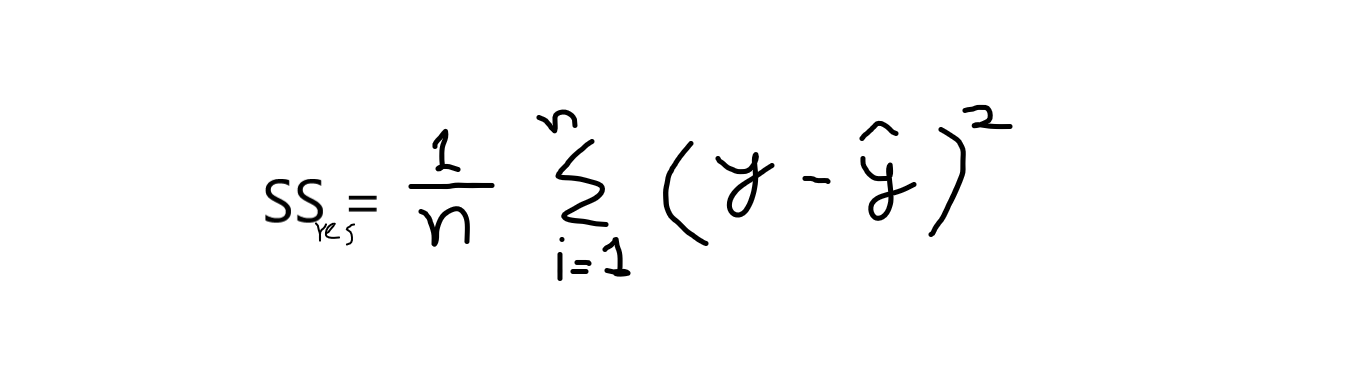
y = valores originales
y ^ = valores predichos. y,
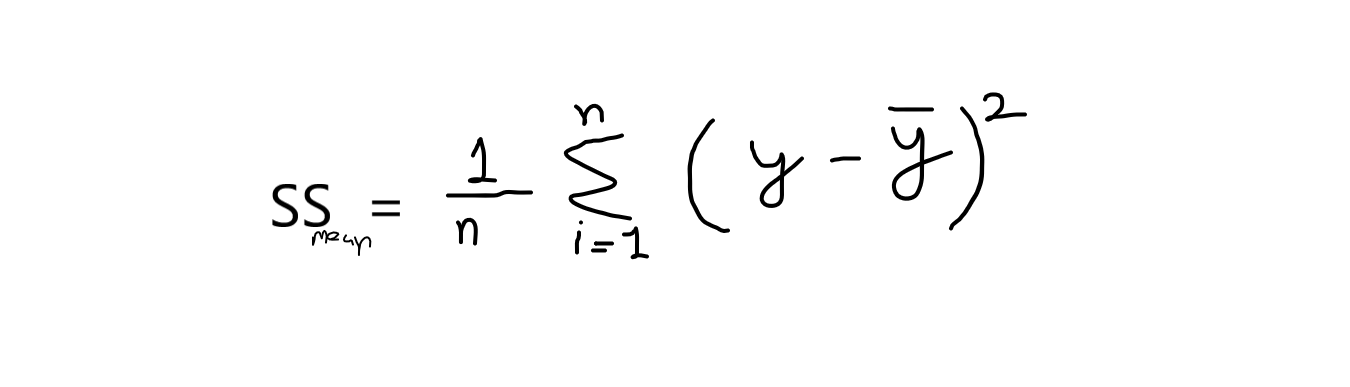
Si tomamos el cálculo de esta ecuación, entonces tenemos que saber que el valor de la suma de las medias es siempre mayor que la suma de los residuales. Si esta condición se cumple, entonces nuestro modelo es bueno para las predicciones. Sus valores oscilan entre 0,0 y 1.
«La proporción de la varianza en la variable dependiente que es predecible a partir de la (s) variable (s) independiente».
La mejor puntuación posible es 1.0 y puede ser negativa porque el modelo puede ser arbitrariamente peor. Un modelo constante que siempre predice el valor esperado de y, sin tener en cuenta las características de entrada, obtendría una puntuación R2 de 0.0.
# importando módulo r2_score
de sklearn.metrics importar r2_score
de sklearn.metrics importar mean_squared_error
# predecir la puntuación de precisión
score = r2_score (y_test, y_prediction)
print (‘r2 socre is’, puntuación)
print (‘mean_sqrd_error is ==’, mean_squared_error (y_test, y_prediction))
print (‘root_mean_squared error of is ==’, np.sqrt (mean_squared_error (y_test, y_prediction)))
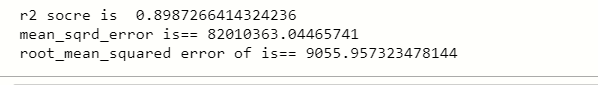
Puede ver que la puntuación de precisión es superior a 0,8, lo que significa que podemos usar este modelo para resolver regresiones lineales múltiples, y también la tasa de error cuadrático medio también es baja.
Notas finales
hola, científicos de datos 😎 arriba tomamos una discusión detallada sobre la regresión lineal múltiple, y el ejemplo que usamos es el ejemplo perfecto de regresión lineal múltiple. Espero que ahora comprenda mejor la regresión lineal múltiple.
¡Espero que hayas disfrutado esto!
Puedes conectarme en LinkedIn: www.linkedin.com/in/mayur-badole-189221199
Además, lea mis otros artículos: https://www.analyticsvidhya.com/blog/author/mayurbadole2407/
Gracias.






