Este artículo fue publicado como parte del Blogatón de ciencia de datos
Introducción
Si comienza a aprender el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud..., lo primero a lo que estará expuesto son los conceptos de álgebra lineal que le brindan una mejor intuición sobre cómo funcionan realmente los algoritmos bajo el capó, lo que le permite tomar mejores decisiones. En Deep Learning, una red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... de avance es una red muy simple y muy útil. Bajo el capó, la red neuronal de alimentación hacia adelante es solo una función compuesta, que multiplica algunas matrices y vectores juntos.
Fuente de imagen: Enlace
No es que los vectores y las matrices sean la única forma de realizar estas operaciones, pero se vuelven altamente eficientes si lo hace. Las estructuras de datos centrales detrás del aprendizaje profundo incluyen
- Escalares
- Vectores,
- Matrices y
- Tensores.
Las operaciones matriciales se utilizan en la descripción de muchos algoritmos de aprendizaje profundo.
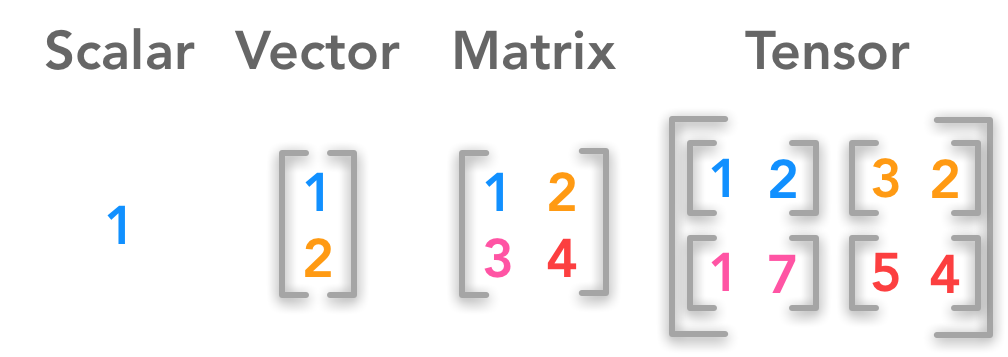
Fuente de imagen: Enlace
Entonces, si realmente quieres ser un profesional en el campo del Deep Learning, no puedes dejar de dominar algunos de estos conceptos. Entonces, en este artículo, discutiremos importantes operaciones matriciales de álgebra lineal que se utilizan en la descripción de métodos de aprendizaje profundo.
Tabla de contenido
Los temas que discutiremos en este artículo son los siguientes:
- ¿Qué son las matrices?
- ¿Cómo sumar y restar diferentes matrices?
- ¿Cómo encontrar la forma y el tamaño de una matriz dada?
- ¿Cómo convertir una matriz densa en una matriz dispersa?
- ¿Cómo encontrar la transposición de una matriz?
- ¿Cómo encontrar la media, la varianza y la desviación estándar de una matriz?
- ¿Cómo encontrar el rastro de una matriz?
- ¿Cómo extraer los elementos mínimos y máximos de una matriz?
- ¿Cómo encontrar el determinante de una matriz?
- ¿Cómo multiplicar las matrices dadas?
- ¿Cómo aplicar la operación particular a cada elemento de una matriz?
- ¿Cómo encontrar la inversa de una matriz?
- ¿Cómo remodelar la matriz a un tamaño diferente?
¿Qué son las matrices?
Las matrices son matrices rectangulares que constan de números y se pueden ver como 2Dakota del Norte-orden de tensores. Si myn son números enteros positivos, es decir, m, n ∈ ℕ entonces la matriz m × n contiene m * n números de elementos, con m número de filas yn número de columnas.
La representación pictórica de una matriz m × n se muestra a continuación:
Fuente de imagen: Enlace
A veces, en lugar de describir los componentes completos de la matriz, usamos la siguiente abreviatura de una matriz:
Por ejemplo-
En este ejemplo, con la ayuda de la biblioteca numpy, crearemos una matriz. Y también verifique la dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y... de la matriz formada.
import numpy as np
matrix = np.array([[45,34],[67,58]])
# Create a matrix
print("The original matrix is given by n", matrix)
# Check the dimension of the matrix
print("The dimension of the given matrix is", matrix.ndim)Producción:
The original matrix is given by [[45 34] [67 58]] The dimension of the given matrix is 2
Suma y resta de matrices
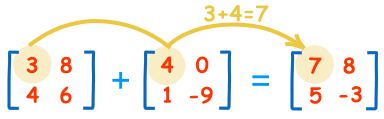
Fuente de imagen: Enlace
En esta sección, realizaremos sumas y restas de matrices usando el los métodos suman y restan. Estos métodos toman dos argumentos y devuelven la suma y la diferencia de esas matrices respectivamente. Si la forma de las matrices no es la misma arroja un error que dice, la suma o resta no es posible.
matrix_1 = np.array([[45,34],[67,58]])
matrix_2 = np.array([[35,24],[57,48]])
# Add the two matrices
print("The result after adding matrix 1 and matrix 2 is given by n" , np.add(matrix_1, matrix_2))
# Subtract one matrix from the other matrices
print("The result after subtracting matrix 1 from matrix 2 is given by n" , np.subtract(matrix_1, matrix_2))
print("The result after subtracting matrix 2 from matrix 1 is given by n" , np.subtract(matrix_2, matrix_1))Producción:
The result after adding matrix 1 and matrix 2 is given by [[ 80 58] [124 106]] The result after subtracting matrix 1 from matrix 2 is given by [[10 10] [10 10]] The result after subtracting matrix 2 from matrix 1 is given by [[-10 -10] [-10 -10]]
Forma y tamaño de una matriz
En esta sección, encontraremos la forma, es decir, el número de filas y columnas en la matriz dada y el tamaño, es decir, el número de elementos en la matriz de una matriz dada.
matrix = np.array([[45,34,75],[67,58,89]])
# Finding number of rows and columns in the matrix
print("The number of rows and columns in the given matrix are " + str(matrix.shape[0]) + " and " + str(matrix.shape[1]) + " respectively")
# Number of elements in the matrix
print("The size of the given matrix is" , matrix.size)Producción:
The number of rows and columns in the given matrix are 2 and 3 respectively The size of the given matrix is 6
Conversión de una matriz densa dada en una matriz dispersa
Primero entendamos qué significa exactamente por matriz dispersa y densa.
Una matriz dispersa es una matriz que consta principalmente de valores cero. Y las matrices dispersas son diferentes de las matrices con valores en su mayoría distintos de cero, que se conocen como matrices densas.
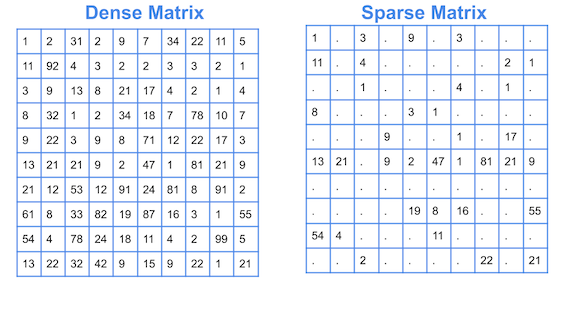
Fuente de imagen: Enlace
from scipy import sparse
# Create a Dense Matrix
dense_matrix = np.array([[0,0],[0,17],[78,0]])
# Convert Dense matrix to Sparse matrix
sparse_matrix = sparse.csr_matrix(dense_matrix)
print("The sparse matrix corresponding to a given dense matrix is given by n" , sparse_matrix)Producción:
The sparse matrix corresponding to a given dense matrix is given by (1, 1) 17 (2, 0) 78
Transposición de matriz
En Matrix Transpose, podemos convertir un vector de fila en un vector de columna y viceversa, es decir, la fila se convierte en columnas y las columnas en filas.
Si tenemos la matriz A = [aij]mxn, entonces la transpuesta de esta matriz es AT = [aji]n × m
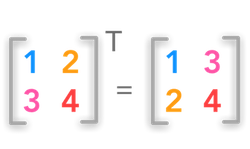Fuente de imagen: Enlace
import numpy as np
matrix = np.array([[45,34],[67,58]])
print("The original matrix is given by n" , matrix)
print("The transpose matrix of the given matrix is n" , matrix.T)Producción:
The original matrix is given by [[45 34] [67 58]] The transpose matrix of the given matrix is [[45 67] [34 58]]
Media, varianza y desviación estándar de una matriz
En esta sección, intentaremos encontrar algunas cosas estadísticas relacionadas con una matriz. Aquí calculamos la media, la varianza y la desviación estándar de la matriz usando las funciones numpy.
import numpy as np
matrix = np.array([[45,34],[67,58], [23,89]])
# Finding the mean of a matrix elements
print("The mean of the elements of a matrix is equal to", np.mean(matrix))
# Finding the Variance of a matrix elements
print("The variance of the elements of a matrix is equal to", np.var(matrix))
# Finding the Standard Deviation of a matrix elements
print("The standard deviation of the elements of a matrix is equal to", np.std(matrix))
print("The standard deviation of the elements of a matrix is equal to", np.sqrt(np.var(matrix)))Producción:
The mean of the elements of a matrix is equal to 52.666666666666664 The variance of the elements of a matrix is equal to 473.5555555555555 The standard deviation of the elements of a matrix is equal to 21.761331658599286 The standard deviation of the elements of a matrix is equal to 21.761331658599286
Rastro de una matriz
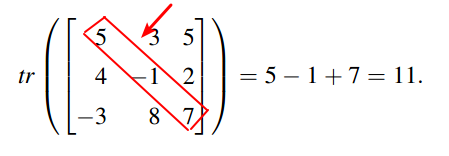
Fuente de imagen: Enlace
En esta sección, intentará encontrar el rastro de una matriz, es decir, la suma de todos los elementos diagonales presentes en una matriz dada.
import numpy as np
matrix = np.array([[1,2,3],[4,5,6], [7,8,9]])
# Get the diagonal elements of a matrix
print("The diagonal elements of a given matrix are n", matrix.diagonal())
# Finding the trace of the matrix
print("The trace of a given matrix is equal to", matrix.diagonal().sum())Producción:
The diagonal elements of a given matrix are [1 5 9] The trace of a given matrix is equal to 15
Encontrar elementos mínimos y máximos de una matriz
En esta sección, intentaremos encontrar los elementos mínimos y máximos de una matriz, es decir, el elemento con el valor más alto y más bajo entre todos los elementos.
import numpy as np
matrix = np.array([[1,2,3],[4,5,6], [7,8,9]])
# Find the minimum element of the matrix
print("The minimum element in a given matrix is", np.min(matrix))
# Find the maximum element of the matrix
print("The maximum element in a given matrix is", np.max(matrix))Producción:
The minimum element in a given matrix is 1 The maximum element in a given matrix is 9
Determinante de una matriz
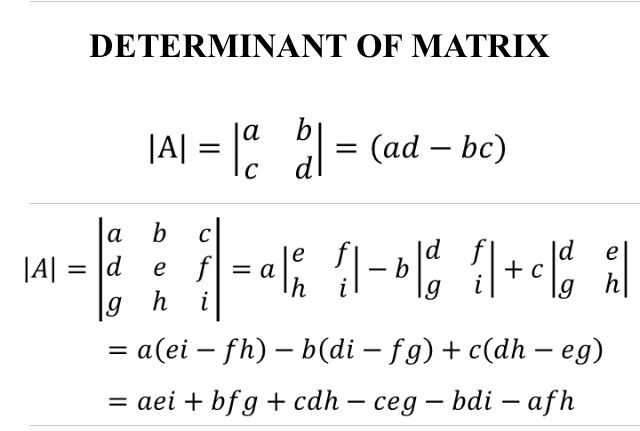
Fuente de imagen: Enlace
En esta sección, intentaremos encontrar el determinante de una matriz. Aquí, para calcular el determinante, usamos el módulo de álgebra lineal presente en el paquete Numpy.
import numpy as np
matrix = np.array([[1,2,4],[3,4,6], [7,8,5]])
# Find the determinant of the matrix
print("The determinant of the given matrix is equal to", np.linalg.det(matrix))Producción:
The determinant of the given matrix is equal to 9.999999999999993
Multiplicación de matrices
Una matriz de forma (mxn) y una matriz B de forma (nxp) multiplicada da C de forma (mxp). Recuerde que al multiplicar las matrices es que el número de columnas en la primera matriz es el mismo que el número de filas en la segunda matriz para realizar la multiplicación sin errores.
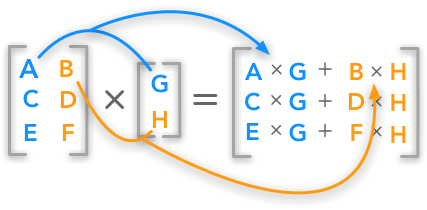
Fuente de imagen: Enlace
En esta sección, intentaremos encontrar la multiplicación de dos matrices.
import numpy as np
matrix_1 = np.array([[45,34],[67,58]])
matrix_2 = np.array([[35,24],[57,48]])
print("The matrix multiplication of given two matrices is given by n", np.matmul(matrix_1, matrix_2))Producción:
The matrix multiplication of given two matrices is given by [[3513 2712] [5651 4392]]
Operaciones inteligentes con elementos usando una función en línea (Lambda)
En este ejemplo, intentaremos agregar un cierto valor a cada uno de los elementos de una matriz.
import numpy as np
matrix = np.array([[1,2,4],[3,4,6], [7,8,5]])
addition = lambda i:i+5
add_5_vec = np.vectorize(addition)
print("The matrix after adding 5 to all its elements is n", add_5_vec(matrix))Producción:
The matrix after adding 5 to all its elements is [[ 6 7 9] [ 8 9 11] [12 13 10]]
Inversa de una matriz
En esta sección, intentaremos encontrar la inversa de una matriz.
import numpy as np
matrix = np.array([[1,2,4],[3,4,6], [7,8,5]])
# Finding the inverse of a matrix
print("The inverse matrix of a given matrix is n", np.linalg.inv(matrix))Producción:
The inverse matrix of a given matrix is [[-2.8 2.2 -0.4] [ 2.7 -2.3 0.6] [-0.4 0.6 -0.2]]
Remodelar una Matriz dada
En esta sección, intentaremos remodelar una matriz dada, es decir, cambiar la forma de la matriz dada. Pero aquí tenemos que notar que el tamaño permanece constante después de remodelar la matriz, es decir, el número de elementos permanece igual.
import numpy as np
matrix = np.array([[1,2,4],[3,4,6],[7,8,5],[9,2,1]])
print("The reshaped matrix is given by n", matrix.reshape(6,2))Producción:
The reshaped matrix is given by [[1 2] [4 3] [4 6] [7 8] [5 9] [2 1]]
Otras publicaciones de blog mías
También puede consultar mis publicaciones de blog anteriores.
Publicaciones anteriores del blog de ciencia de datos.
Aquí está mi perfil de Linkedin en caso de que quieras conectarte conmigo. Estaré feliz de estar conectado contigo.
Correo electrónico
Para cualquier consulta, puede enviarme un correo electrónico al Gmail.
Notas finales
¡Gracias por leer!
Espero que les haya gustado el artículo. Si te gusta, compártelo con tus amigos también. ¿Algo no mencionado o quieres compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted. 😉
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.
