Algoritmo de regresión lineal para hacer predicciones fácilmente

Este artículo fue publicado como parte del Blogatón de ciencia de datos

Introducción

. Un problema de regresión es cuando la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de salida es un valor real o continuo.

En Regresión, trazamos un gráfico entre las variables que mejor se ajustan a los puntos de datos dados. El modelo de aprendizaje automático puede ofrecer predicciones sobre los datos. En palabras ingenuas, «La regresión muestra una línea o curva que pasa por todos los puntos de datos en un gráfico de predicción de objetivos de tal manera que la distancia vertical entre los puntos de datos y la línea de regresión es mínima». Se utiliza principalmente para predecir, pronosticar, modelar series de tiempo y determinar la relación causal-efecto entre variables.

Tipos de modelos de regresión

1. Regresión lineal
2. Regresión polinomial
3. Regresión logística

Regresión lineal

La regresión lineal es un método de regresión estadística simple y silencioso que se utiliza para el análisis predictivo y muestra la relación entre las variables continuas. La regresión lineal muestra la relación lineal entre la variable independiente (eje X) y la variable dependiente (eje Y), en consecuencia llamada regresión lineal. Si hay una sola variable de entrada (x), dicha regresión lineal se llama Regresión lineal simple. Y si hay más de una variable de entrada, dicha regresión lineal se llama regresión lineal múltiple. El modelo de regresión lineal da una línea recta inclinada que describe la relación dentro de las variables.

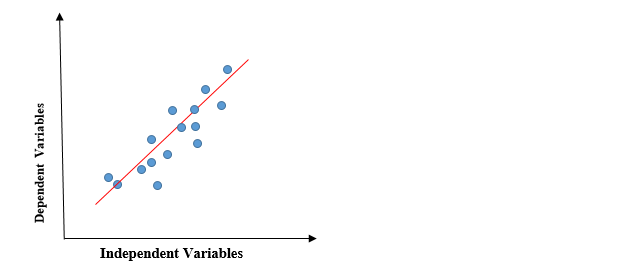
El gráfico anterior presenta la relación lineal entre la variable dependiente y las variables independientes. Cuando el valor de x (variable independiente) aumenta, el valor de y (variable dependiente) también está aumentando. La línea roja se conoce como la línea recta de mejor ajuste. Con base en los puntos de datos dados, intentamos trazar una línea que modele mejor los puntos.

Para calcular la regresión lineal de línea de mejor ajuste, se utiliza una forma tradicional de pendiente-intersección.

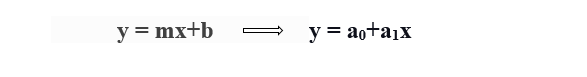
y = Variable dependiente.

x = Variable independiente.

a0 = intersección de la línea.

a1 = Coeficiente de regresión lineal.

Necesidad de una regresión lineal

Como se mencionó anteriormente, la regresión lineal estima la relación entre una variable dependiente y una variable independiente. Entendamos esto con un ejemplo sencillo:

Digamos que queremos estimar el salario de un empleado en función del año de experiencia. Tienes los datos recientes de la empresa, lo que indica que la relación entre experiencia y salario. Aquí el año de experiencia es una variable independiente y el salario de un empleado es una variable dependiente, ya que el salario de un empleado depende de la experiencia de un empleado. Con esta información, podemos predecir el salario futuro del empleado en función de la información actual y pasada.

Una línea de regresión puede ser una relación lineal positiva o una relación lineal negativa.

Relación lineal positiva

Si la variable dependiente se expande en el eje Y y la variable independiente progresa en el eje X, dicha relación se denomina relación lineal positiva.

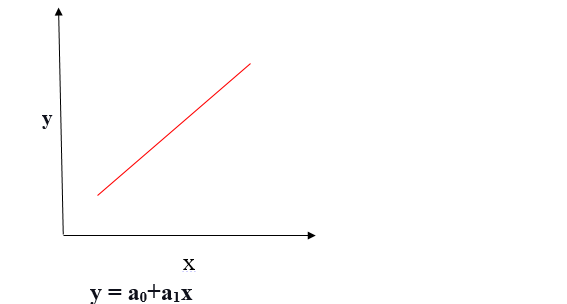
Relación lineal negativa

Si la variable dependiente disminuye en el eje Y y la variable independiente aumenta en el eje X, dicha relación se denomina relación lineal negativa.

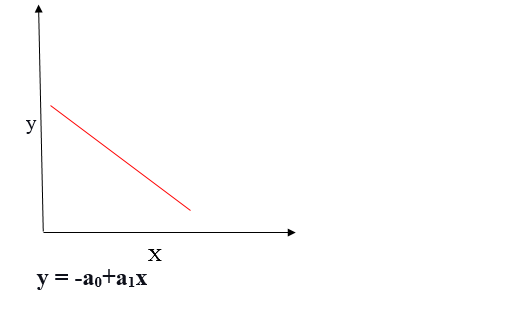
El objetivo del algoritmo de regresión lineal es obtener los mejores valores para a0 y a1 para encontrar la línea de mejor ajuste. La línea de mejor ajuste debe tener el menor error, lo que significa que el error entre los valores predichos y los valores reales debe minimizarse.

Función de costo

La función de costo ayuda a determinar los mejores valores posibles para a0 y a1, lo que proporciona la línea de mejor ajuste para los puntos de datos.

La función de costo optimiza los coeficientes de regresión o ponderaciones y mide cómo se está desempeñando un modelo de regresión lineal. La función de costo se usa para encontrar la precisión de la función de mapeo que asigna la variable de entrada a la variable de salida. Esta función de mapeo también se conoce como la función de hipótesis.

En regresión lineal, Error cuadrático medio (MSE) Se utiliza la función de costo, que es el promedio del error al cuadrado que se produjo entre los valores predichos y los valores reales.

Por ecuación lineal simple y = mx + b podemos calcular MSE como:

Vamos a y = valores reales, y_I = valores predichos

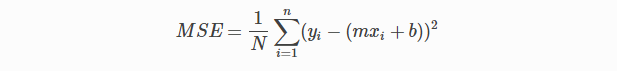
Usando la función MSE, cambiaremos los valores de a0 y a1 de manera que el valor MSE se establezca en los mínimos. ParámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... del modelo xi, b (a₀,a₁) se puede manipular para minimizar la función de costo. Estos parámetros se pueden determinar utilizando el método de descenso de gradiente para que el valor de la función de costo sea mínimo.

Descenso de gradiente

El descenso de gradiente es un método de actualización de a0 y a1 para minimizar la función de costo (MSE). Un modelo de regresión usa el descenso de gradiente para actualizar los coeficientes de la línea (a0, a1 => xi, b) al reducir la función de costo mediante una selección aleatoria de valores de coeficiente y luego actualizar iterativamente los valores para alcanzar la función de costo mínimo.

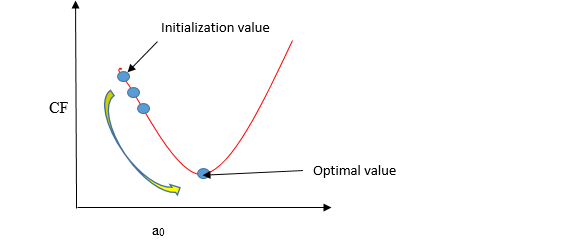
Imagina un pozo en forma de U. Estás parado en el punto más alto del pozo y tu objetivo es llegar al fondo del pozo. Hay un tesoro, y solo puedes dar un número discreto de pasos para llegar al fondo. Si decides dar un paso a la vez, eventualmente llegarás al fondo del pozo, pero esto tomará más tiempo. Si elige dar pasos más largos cada vez, puede llegar antes, pero existe la posibilidad de que pueda sobrepasar el fondo del pozo y no cerca del fondo. En el algoritmo de descenso de gradiente, la cantidad de pasos que da es la tasa de aprendizaje, y esto decide qué tan rápido converge el algoritmo a los mínimos.

Para actualizar un₀ y un₁, tomamos gradientes de la función de costo. Para encontrar estos gradientes, tomamos derivadas parciales para un₀ y un₁.

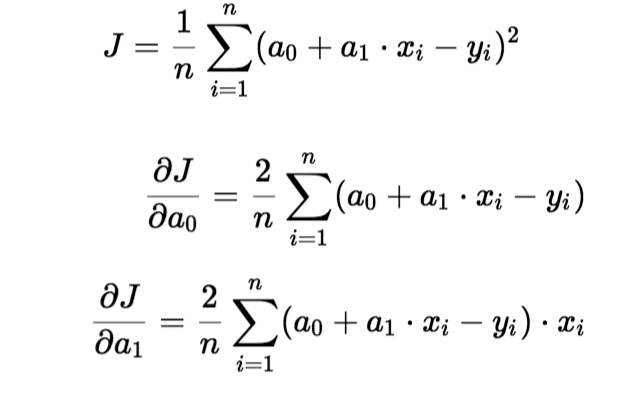
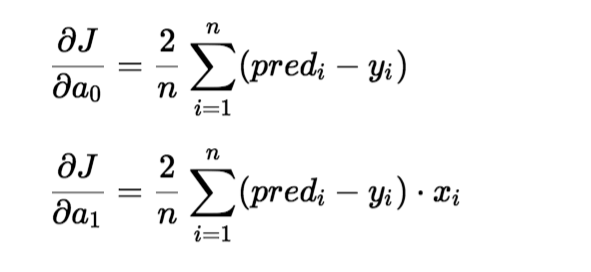
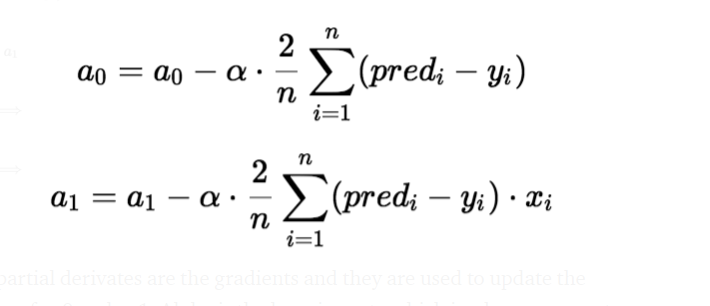
Las derivadas parciales son los gradientes y se utilizan para actualizar los valores de un₀ y un₁. Alpha es la tasa de aprendizaje.

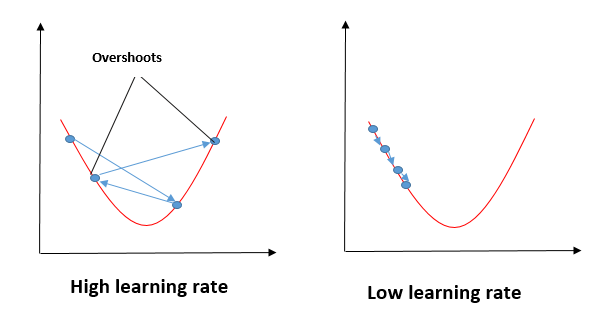
Impacto de diferentes valores para la tasa de aprendizaje

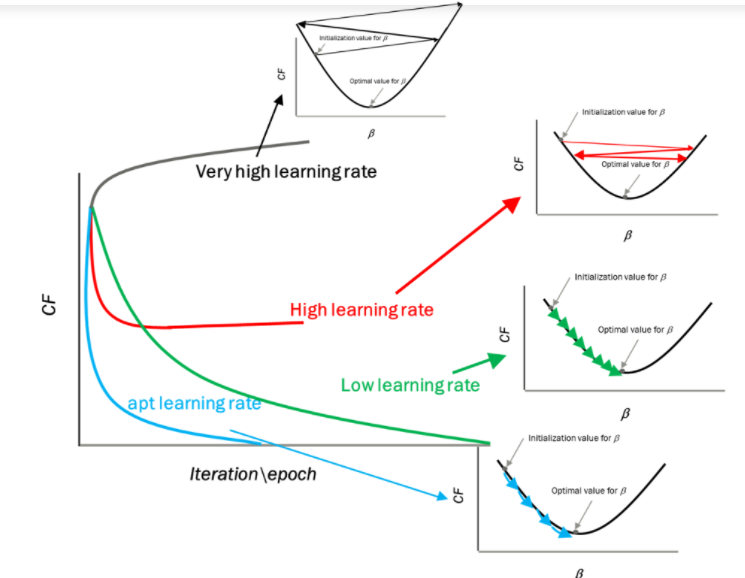
Fuente: mygreatleaning.com

La línea azul representa el valor óptimo de la tasa de aprendizaje y el valor de la función de costo se minimiza en unas pocas iteraciones. La línea verde representa si la tasa de aprendizaje es menor que el valor óptimo, entonces el número de iteraciones requeridas es alto para minimizar la función de costo. Si la tasa de aprendizaje seleccionada es muy alta, la función de costo podría continuar aumentando con iteraciones y saturarse a un valor superior al valor mínimo, el representado por una línea roja y negra.

Caso de uso

En esto, tomaré números aleatorios para la variable dependiente (salario) y una variable independiente (experiencia) y predeciré el impacto de un año de experiencia en el salario.

Pasos para implementar el modelo de regresión lineal

importar algunas bibliotecas requeridas

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

Definir el conjunto de datos

x= np.array([2.4,5.0,1.5,3.8,8.7,3.6,1.2,8.1,2.5,5,1.6,1.6,2.4,3.9,5.4])
y = np.array([2.1,4.7,1.7,3.6,8.7,3.2,1.0,8.0,2.4,6,1.1,1.3,2.4,3.9,4.8])
n = np.size(x)

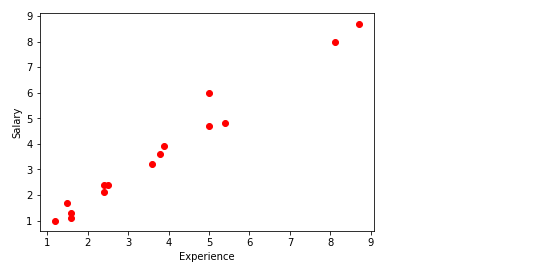
Trazar los puntos de datos

plt.scatter(experience,salary, color="red")
plt.xlabel("Experience")
plt.ylabel("Salary")
plt.show()

La función principal para calcular valores de coeficientes.

1. Inicialice los parámetros.
2. Predecir el valor de una variable dependiente dada una variable independiente.
3. Calcule el error en la predicción para todos los puntos de datos.
4. Calcule la derivada parcial wrt a0 y a1.
5. Calcula el costo de cada número y súmalos.
6. Actualice los valores de a0 y a1.

#initialize the parameters
a0 = 0                  #intercept
a1 = 0                  #Slop
lr = 0.0001             #Learning rate
iterations = 1000       # Number of iterations
error = []              # Error array to calculate cost for each iterations.
for itr in range(iterations):
    error_cost = 0
    cost_a0 = 0
    cost_a1 = 0
    for i in range(len(experience)):
        y_pred = a0+a1*experience[i]   # predict value for given x
        error_cost = error_cost +(salary[i]-y_pred)**2
        for j in range(len(experience)):
            partial_wrt_a0 = -2 *(salary[j] - (a0 + a1*experience[j]))                #partial derivative w.r.t a0
            partial_wrt_a1 = (-2*experience[j])*(salary[j]-(a0 + a1*experience[j]))   #partial derivative w.r.t a1
            cost_a0 = cost_a0 + partial_wrt_a0      #calculate cost for each number and add
            cost_a1 = cost_a1 + partial_wrt_a1      #calculate cost for each number and add
        a0 = a0 - lr * cost_a0    #update a0
        a1 = a1 - lr * cost_a1    #update a1
        print(itr,a0,a1)          #Check iteration and updated a0 and a1
    error.append(error_cost)      #Append the data in array

En una iteración aproximada de 50-60, obtuvimos el valor de a0 y a1.

print(a0)
print(a1)

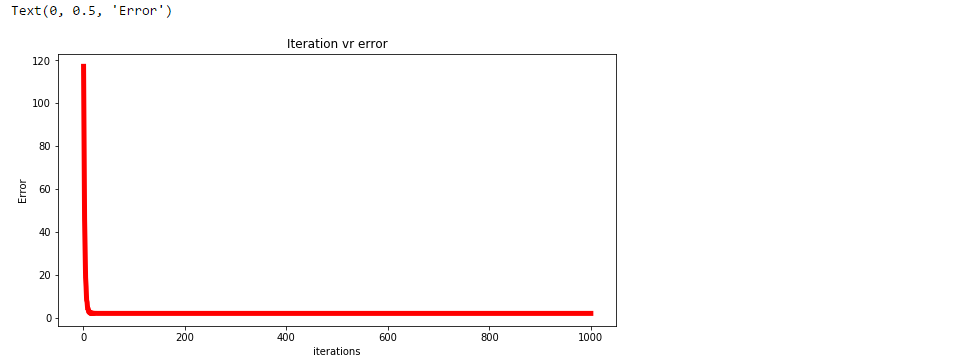
Trazar el error para cada iteración.

plt.figure(figsize=(10,5))
plt.plot(np.arange(1,len(error)+1),error,color="red",linewidth = 5)
plt.title("Iteration vr error")
plt.xlabel("iterations")
plt.ylabel("Error")

Predecir los valores.

pred = a0+a1*experience
print(pred)

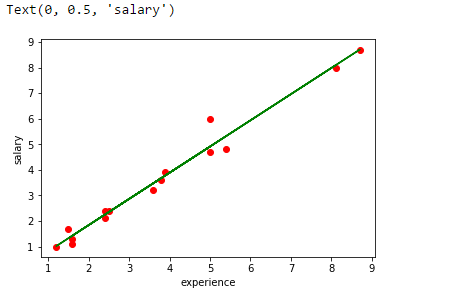
Trace la línea de regresión.

plt.scatter(experience,salary,color="red")
plt.plot(experience,pred, color="green")
plt.xlabel("experience")
plt.ylabel("salary")

Analice el rendimiento del modelo calculando el error cuadrático medio.

error1 = salary - pred
se = np.sum(error1 ** 2)
mse = se/n
print("mean squared error is", mse)

Utilice la biblioteca scikit para confirmar los pasos anteriores.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error 
experience = experience.reshape(-1,1)
model = LinearRegression()
model.fit(experience,salary)
salary_pred = model.predict(experience)
Mse = mean_squared_error(salary, salary_pred)
print('slop', model.coef_)
print("Intercept", model.intercept_)
print("MSE", Mse)

Resumen

En Regresión, trazamos un gráfico entre las variables que mejor se ajustan a los puntos de datos dados. La regresión lineal muestra la relación lineal entre la variable independiente (eje X) y la variable dependiente (eje Y).Para calcular la regresión lineal de línea de mejor ajuste, se utiliza una forma tradicional de pendiente-intersección. Una línea de regresión puede ser una relación lineal positiva o una relación lineal negativa.

El objetivo del algoritmo de regresión lineal es obtener los mejores valores para a0 y a1 para encontrar la línea de mejor ajuste y la línea de mejor ajuste debe tener el menor error. En regresión lineal, Error cuadrático medio (MSE) se utiliza la función de coste, que ayuda a determinar los mejores valores posibles para a0 y a1, lo que proporciona la línea de mejor ajuste para los puntos de datos. Usando la función MSE, cambiaremos los valores de a0 y a1 de manera que el valor MSE se establezca en los mínimos. El descenso de gradiente es un método para actualizar a0 y a1 para minimizar la función de costo (MSE)

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado