Simulación de Monte Carlo | Realizar simulación de Monte Carlo en R

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Introducción

Este artículo tiene como objetivo presentar la simulación de Monte Carlo para el análisis de incertidumbre variable. Monte Carlo puede reemplazar la propagación del error porque supera las desventajas de la propagación del error. Discutiremos:

• Cómo realizar la propagación del error;
• ¿Por qué utilizar Monte Carlo en lugar de la propagación del error? y
• Los pasos para realizar la incertidumbre de Montecarlo.

Comencemos esta discusión con cosas simples. ¿Cuánto gasta un empleado de la ciudad A en gastos de manutención en un mes? Hay miles de empleados en la ciudad A con diferentes gastos de manutención. Para responder a la pregunta anterior, debemos preguntar a varios empleados y registrar sus respuestas. Esos empleados responderán de manera diferente. Sus gastos de manutención variarán en una distribución de probabilidad. Aunque no tenemos los recursos para preguntar a todos los empleados, podemos muestrear un grupo de, por ejemplo, 50 empleados para que la encuesta represente a la población.

Sin embargo, todavía necesitamos un número para representar el gasto de vida total. Digamos que obtenemos que el gasto de vida mensual promedio es de $ 2000. O bien, otra forma es utilizar la mediana para representar el gasto total. Para expresar otros posibles gastos de manutención, podemos usar la desviación estándar. Por ejemplo, el gasto de vida mensual en la ciudad A es de $ 2000 ± 500 (promedio ± desviación estándar).

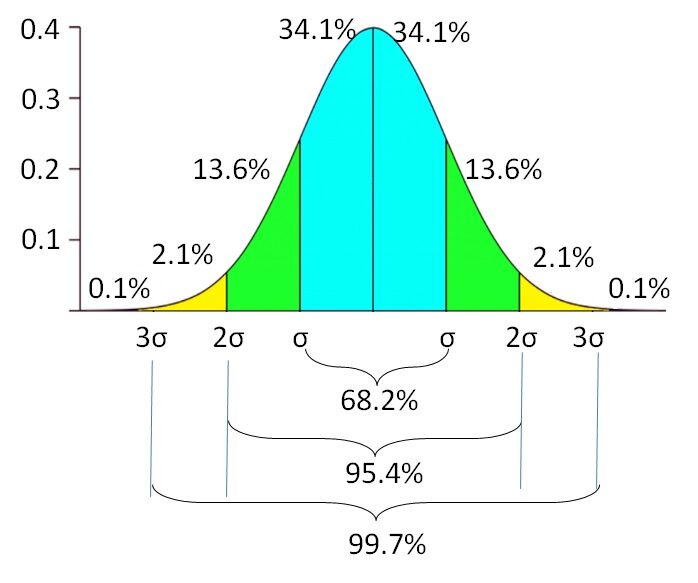
Significa que si los datos se distribuyen normalmente, el 68,2% de los empleados gastan entre $ 1500 y $ 2500. Hay otro 31,8% de los empleados que gastan menos de $ 1500 y más de $ 2500 en costos de vida mensuales. La probabilidad del gasto de vida disminuye a medida que se aleja del promedio. Existe una probabilidad del 0,1% de encontrar empleados con gastos de subsistencia inferiores a $ 500 o superiores a $ 3500. La desviación estándar refleja la incertidumbre variable del gasto de vida. Indica la extensión inferior y superior de la variable, en lugar de depender de un solo valor.

Propagación del error

Dado que los empleados de la ciudad A tienen ingresos: $ 3200 ± 2000, gastos de manutención: $ 2000 ± 500, crédito: $ 180 ± 130, ingresos o gastos inesperados: $ 20 ± 300 y tasa de interés bancaria: 0,85 ± 0,35% mensual. Queremos calcular cuánto puede ahorrar un empleado en un mes. La ecuación se expresa a continuación:

Ahorro = (Ingresos – Gastos_ de vida – Crédito + Ingresos / gastos inesperados) × (1 + Intereses)

El ahorro mensual se calcula como el ingreso total deducido de los gastos de manutención y el crédito y se suma a los ingresos o gastos inesperados. Después de un mes, el ahorro nominal aumenta debido al interés bancario. Calcularemos la media de ahorro mensual y la incertidumbre. Observe la siguiente ecuación sobre cómo calcular la incertidumbre.

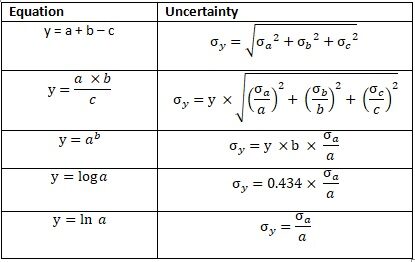
Fig.2 Propagación del error

Saving1 = ((3200 ± 2000) - (2000 ± 500) - (180 ± 130) + (20 ± 300)) × (1 + (0.0085 ± 0.0035))

Saving1 = 1040 ± σSaving_1

σSaving_1 = ((20002 + 5002 + 1302 + 20002))0.5

σSaving_1 = 2087

Saving1 ± σSaving_1 = 1040 ± 2087

Esto calcula el ahorro mensual después de contabilizar el interés bancario.

Saving = Saving1 × (1 + (0.0085 ± 0.0035)) 

Saving = (1040 ± 2087) × (1.0085 ± 0.0035)

Saving = 1049 ± σSaving_2

σSaving = 1049 × ((2087/1040)2 + (0.0035/1.0085)2)0.5

σSaving = 1049 × 2.01

σSaving = 2105

Ahorro ± σ_Ahorro = 1049 ± 2105

A partir del resultado, podemos ver que, en promedio, las personas pueden ahorrar $ 1049 en un mes con la incertidumbre de $ 2105. El límite inferior del ahorro mensual es – $ 1056 ($ 1049 – $ 2105), que es un valor negativo. La incertidumbre en sí es 2105, que es 2 veces mayor que el valor medio. Si visualizamos el gráfico, podemos ver que los ahorros de los empleados oscilan entre – $ 6000 y $ 8000. Parece extraño porque los límites inferior y superior están casi equilibrados. Creo que, en realidad, el monto del ahorro debería tener una mayor variabilidad que el monto del déficit.

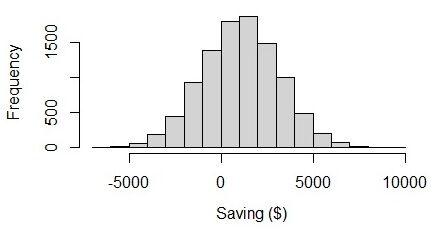
Fig.3 Visualización del ahorro en una distribución normal

¿Cómo está pasando esto? El problema está en los datos de ingresos. El ingreso de $ 3200 ± 2000 tiene una alta incertidumbre debido a la variabilidad del ingreso. La incertidumbre es más de un tercio del valor medio. Si asumimos que esta es una distribución normal, veremos que el 4.8% de la población tiene ingresos por debajo de 0, lo que no parece probable que suceda. De hecho, los ingresos deben estar siempre por encima de% 0. Este problema ocurre cuando asumimos que todas las variables están distribuidas normalmente, pero en realidad no lo están.

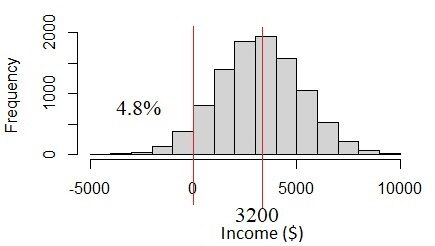
Fig.4 Distribución normal si la desviación estándar del ingreso es demasiado grande

Simulación del Monte Carlo

¿Cuál es la solución? Otra forma de evaluar la incertidumbre es aplicando la simulación de Monte Carlo. Monte Carlo es originalmente el nombre de un área administrativa en Mónaco. Pero el Montecarlo de nuestra discusión de hoy es material estadístico. Monte Carlo puede superar la desventaja de la propagación de errores. La simulación de Monte Carlo, a diferencia de la propagación del error, puede funcionar en una distribución de datos que no sea la distribución normal y en datos con una gran desviación estándar.

Fig.5 Monte Carlo en Mónaco. Fuente: Mapa de Google

La simulación de Monte Carlo simula o genera un conjunto de números aleatorios de acuerdo con la distribución de datos y los parámetros de cada variable. Una vez generados, todos los valores de las variables se calculan utilizando la ecuación. Esto suena un poco más complicado que usar la propagación del error. Pero usar herramientas de ciencia de datos, como Python o R, será muy simple. En esta discusión, demostraremos el uso del lenguaje estadístico R.

Pasos para realizar una simulación de Monte Carlo

1. Verifique la función de densidad de probabilidad de la distribución de datos.

Digamos que examinamos el registro de datos proporcionado por la encuesta de 50 encuestados. Hay muchos tipos de funciones de densidad de probabilidad y tenemos que determinar cuál se ajusta a nuestros datos. Las variables con distribución normal son solo gastos de manutención e ingresos o gastos inesperados. La distribución de los datos de ingresos es positiva.

En este caso, lo trataremos como una distribución gamma. Esta es la razón por la que el promedio y la propagación del error no son adecuados para estos datos. Las otras dos variables tampoco tienen una distribución normal. La tasa de interés bancaria se distribuye uniformemente entre 0,3 y 1,5.

La distribución de datos de los préstamos para pagar el crédito es bastante singular. Los datos se distribuyen principalmente en dos grupos de población. El primer grupo tiene menos crédito que el segundo. Digamos que la distribución de datos del crédito no se ajusta a ninguna función de densidad de probabilidad. Luego, usaremos una distribución no paramétrica.

2. Generar simulación de Monte Carlo

Generar simulación Monte Carlo significa generar un conjunto de números aleatorios con la misma distribución de datos que los datos originales. Para hacer esto, simplemente establecemos el número de simulaciones y los parámetros de distribución de acuerdo con el tipo de distribución. Establecimos el número de simulaciones en 10,000. Significa que simularemos los datos de 50 encuestados en 10,000 datos.

Los parámetros de la distribución normal son media / media y desviación estándar. Sabemos que los promedios ± desviaciones estándar de los gastos de manutención y los ingresos o resultados inesperados son 2000 ± 500 y 20 ± 300 respectivamente. Ahora, podemos generar las distribuciones. En este artículo, usaré el lenguaje R. Por supuesto, otros lenguajes de ciencia de datos, como Python, también pueden hacerlo. Vea que los datos simulados tienen una media y estándar similar, no igual, que los parámetros de entrada.

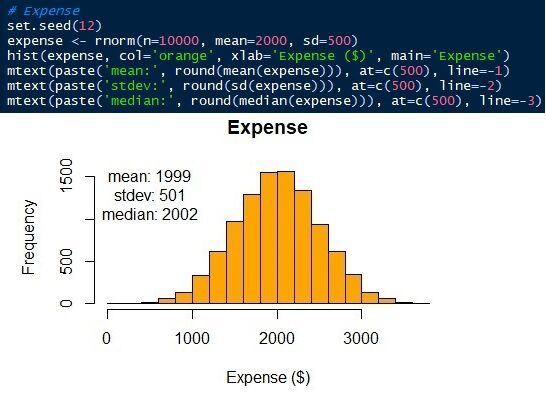
Fig.6 Distribución normal del gasto de vida

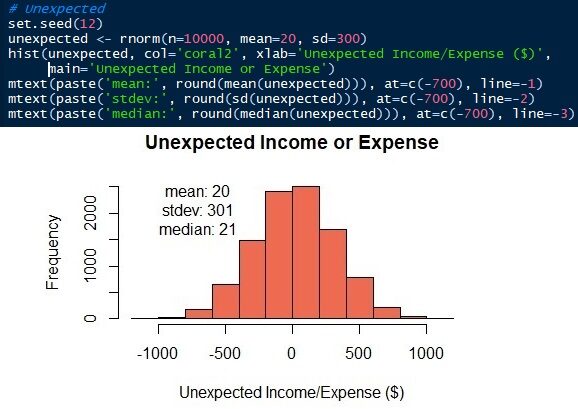
Fig.7 Distribución normal de ingresos o gastos inesperados

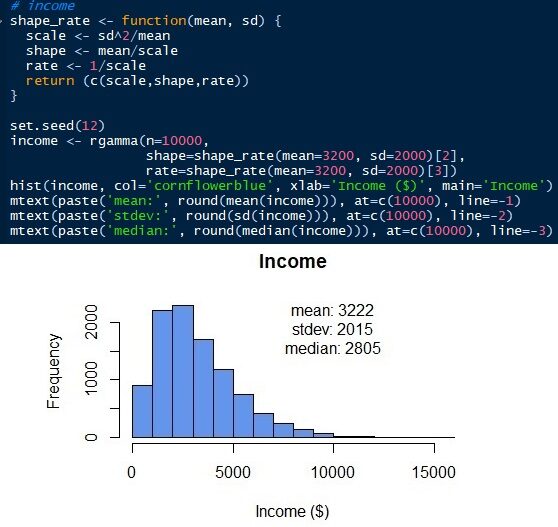
Para generar la distribución gamma, necesitamos conocer otros parámetros. A diferencia de la distribución normal, la distribución gamma tiene escala, forma y velocidad como parámetros. Pero podemos obtener esos parámetros con la desviación estándar y media (de). Escala = sd²/significar. Forma = media / escala. Tasa = 1 / escala. Luego, podemos simular la distribución gamma de los ingresos de los empleados como se muestra a continuación. La distribución gamma solo puede tener valores positivos. No hay ningún valor por debajo de 0 ya que los ingresos de todos los empleados deben ser un número positivo. La distribución normal daría valores negativos si el error estándar es demasiado grande. Vea que la distribución simulada tiene una desviación media y estándar de 3222 y 2015 respectivamente, que están cerca de los parámetros de entrada originales. Pero tenemos una mediana de 2805. La mediana de la distribución gamma, a diferencia de la distribución normal, está lejos de la media.

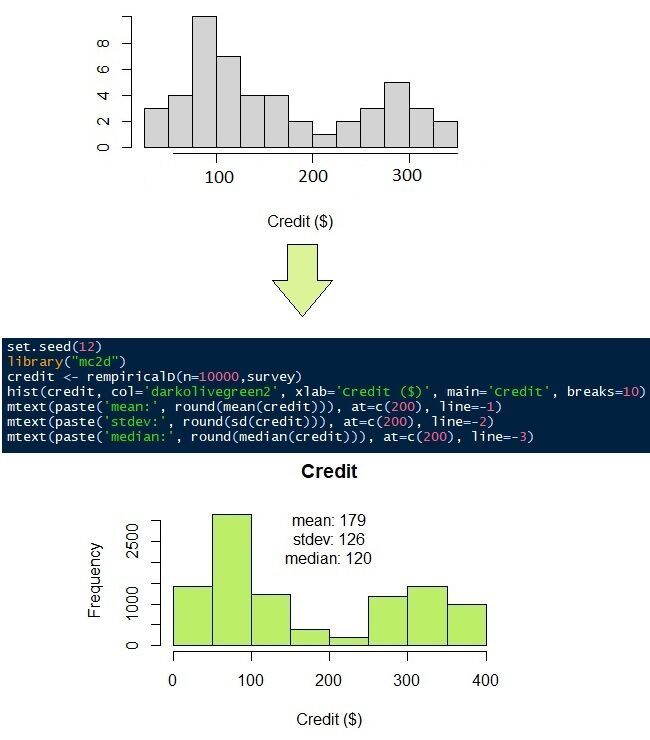
El crédito para pagar mensual, como se mencionó anteriormente, no tiene una función de densidad de probabilidad adecuada. Eche un vistazo a las respuestas de 50 encuestas en la Figura 9 (histograma gris). Parece que la mayoría de la gente tiene que pagar su crédito de $ 100 y $ 300. Para simular las 50 observaciones en 10,000 observaciones, podemos usar una distribución no paramétrica. Como sugiere su nombre, la distribución no paramétrica no requiere parámetros, como la media, la desviación estándar, la forma o la tasa, como lo hacen las distribuciones normal y gamma. Requiere solo los datos originales.

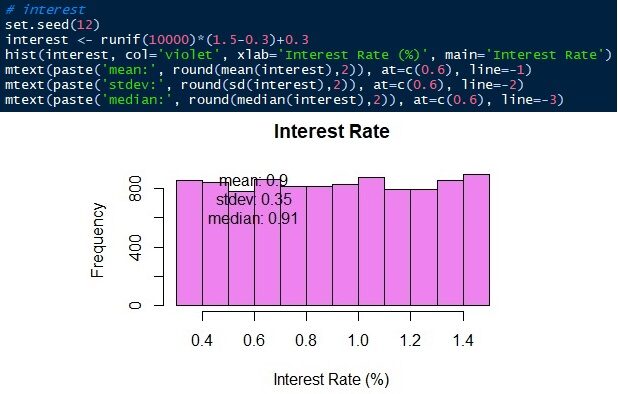
La última variable a simular es la tasa de interés bancaria. La tasa de interés bancaria varía de 0,3 a 1,5 de manera uniforme. Simularemos 10,000 observaciones que van desde 0.3 a 1.5 con la misma probabilidad.

3. Combinación de las simulaciones de Monte Carlo

El último paso es combinar las Simulaciones de Monte Carlo utilizando la ecuación para calcular el ahorro mensual. Para hacer esto, solo necesitamos juntar todas las simulaciones en una tabla. Luego, podemos calcular 10,000 filas de ahorros mensuales. El resultado es $ 1073 ± 2052, no muy diferente de la propagación del error. Pero, la simulación de Monte Carlo muestra la densidad de probabilidad. Podemos ver que la mediana de ahorro es de $ 666 y los datos oscilan entre $ 2000 y 10000.

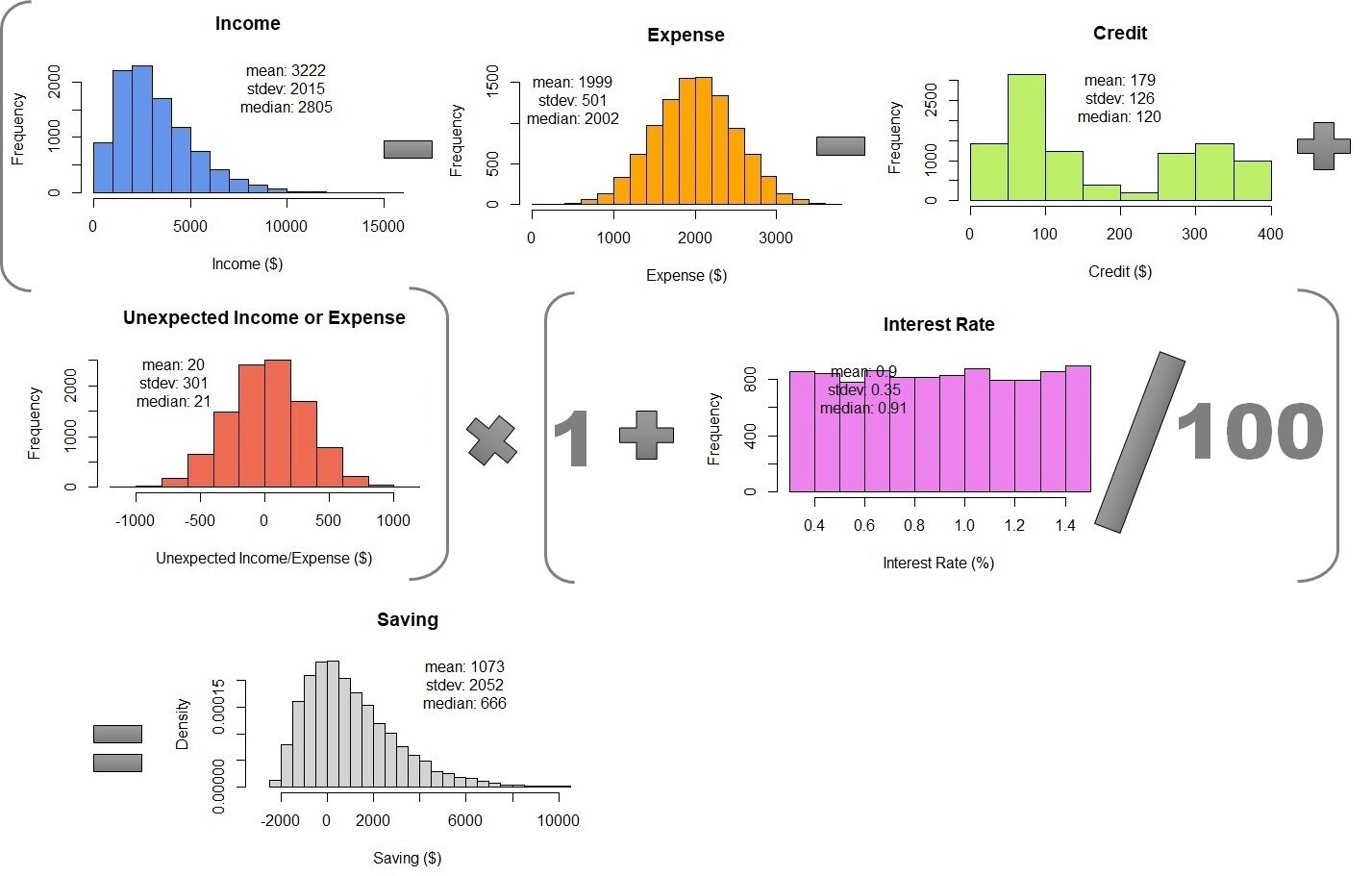
Tabla 1 – Combinación de simulaciones de Monte Carlo

Ahora, veamos otro ejemplo con variabilidad espacial y temporal. La tarea consiste en calcular la escorrentía superficial de una cuenca. La cuenca es el límite de la hidrología de las aguas superficiales. Toda la lluvia que cae debajo de la cuenca no cruzará fuera del límite. Parte de la lluvia se infiltra en el suelo de acuerdo con el tamaño de las partículas del suelo y el tipo de cobertura terrestre. El agua que no se infiltra en el suelo se llama escorrentía superficial. La escorrentía superficial fluirá hacia el río como descarga del río.

La siguiente tabla muestra la intensidad de lluvia mensual en un año y el coeficiente de escorrentía en un 1,5 km.² cuenca. La incertidumbre puede deberse a la heterogeneidad espacial y temporal. El coeficiente de precipitación y escorrentía (debido al suelo y al tipo de cobertura terrestre) varía espacialmente en la cuenca. La precipitación de la cuenca se mide con varios pluviómetros. Dan precipitaciones medias con incertidumbre debido a la distribución espacial. La distribución de la cobertura terrestre también da la incertidumbre del coeficiente de escorrentía.

Un coeficiente de escorrentía es la proporción de lluvia que no se infiltra en el suelo y se convierte en escorrentía superficial. El tipo de suelo forestal o grueso tiene un bajo coeficiente de escorrentía. Los asentamientos o casas tienen un alto coeficiente de escorrentía. La conversión de la cubierta terrestre del bosque en asentamientos aumenta el coeficiente de escorrentía porque una mayor proporción de agua de lluvia será una escorrentía superficial.

La variabilidad temporal también ocurre debido a que las lluvias en las estaciones húmeda y seca son diferentes. El cambio de la cobertura terrestre a lo largo del tiempo también provoca la variabilidad temporal del coeficiente de escorrentía. Otras fuentes de incertidumbre son la calidad de las herramientas de medición, los métodos de medición, las condiciones ambientales y otras condiciones inexplicables debido a la falta de conocimiento.

Mes	Precipitaciones (mm / mes)	Coeficiente de escorrentía	Área (km2)
ene	320 ± 37	0,3 ± 0,2	1,5
feb	350 ± 59	0,3 ± 0,2	1,5
mar	205 ± 26	0,4 ± 0,1	1,5
abr	170 ± 41	0,4 ± 0,1	1,5
Mayo	106 ± 48	0,4 ± 0,1	1,5
jun	91 ± 32	0,4 ± 0,1	1,5
jul	77 ± 16	0,4 ± 0,1	1,5
ago	52 ± 15	0,7 ± 0,2	1,5
sep	100 ± 50	0,7 ± 0,2	1,5
oct	120 ± 46	0,7 ± 0,2	1,5
nov	253 ± 45	0,7 ± 0,2	1,5
dic	210 ± 48	0,7 ± 0,2	1,5

La ecuación es escorrentía superficial = intensidad de lluvia × coeficiente de escorrentía × área de la cuenca. Toda la distribución se simula utilizando una distribución gamma. La escorrentía superficial promedio mensual es de 124.000 ± 30 m³/mes. La mediana es de 120.000 m³/mes.

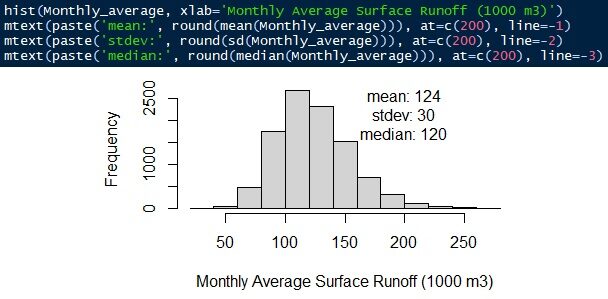
Fig.12 Escorrentía superficial promedio mensual

sobre el autor

Conéctate conmigo aquí https://www.linkedin.com/in/rendy-kurnia/

Relacionado