Introducción
Los algoritmos de aprendizaje automático se clasifican en tres tipos: aprendizaje supervisadoEl aprendizaje supervisado es un enfoque de machine learning donde un modelo se entrena utilizando un conjunto de datos etiquetados. Cada entrada en el conjunto de datos está asociada a una salida conocida, lo que permite al modelo aprender a predecir resultados para nuevas entradas. Este método es ampliamente utilizado en aplicaciones como la clasificación de imágenes, el reconocimiento de voz y la predicción de tendencias, destacando su importancia en..., aprendizaje no supervisadoEl aprendizaje no supervisado es una técnica de machine learning que permite a los modelos identificar patrones y estructuras en datos sin etiquetas predefinidas. A través de algoritmos como k-means y análisis de componentes principales, este enfoque se utiliza en diversas aplicaciones, como la segmentación de clientes, la detección de anomalías y la compresión de datos. Su capacidad para revelar información oculta lo convierte en una herramienta valiosa en la... y aprendizaje reforzado. La agrupación en clústeres de K-significa es una técnica de aprendizaje automático no supervisada. Cuando no se proporciona la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de salida o respuesta, este algoritmo se utiliza para categorizar los datos en grupos distintos para comprenderlos mejor. También se conoce como un enfoque de aprendizaje automático basado en datos, ya que agrupa datos en función de patrones ocultos, conocimientos y similitudes en los datos.
Considere el siguiente diagrama: si se le pide que agrupe a las personas en la imagen en diferentes grupos o grupos y no sabe nada sobre ellos, sin duda intentará localizar las cualidades, características o atributos físicos que estas personas comparten. Después de observar a estas personas, se llega a la conclusión de que se pueden segregar en función de su altura y ancho; dado que no tienes conocimiento previo sobre estas personas. La agrupación en clústeres de k-means ejecuta un trabajo aproximadamente equivalente. Intenta clasificar los datos en grupos basados en similitudes y patrones ocultos. «K» en agrupación de K-medias se refiere al número de agrupaciones que el algoritmo generará en los datos.
Agrupación de K-Means: ¿Cómo funciona?
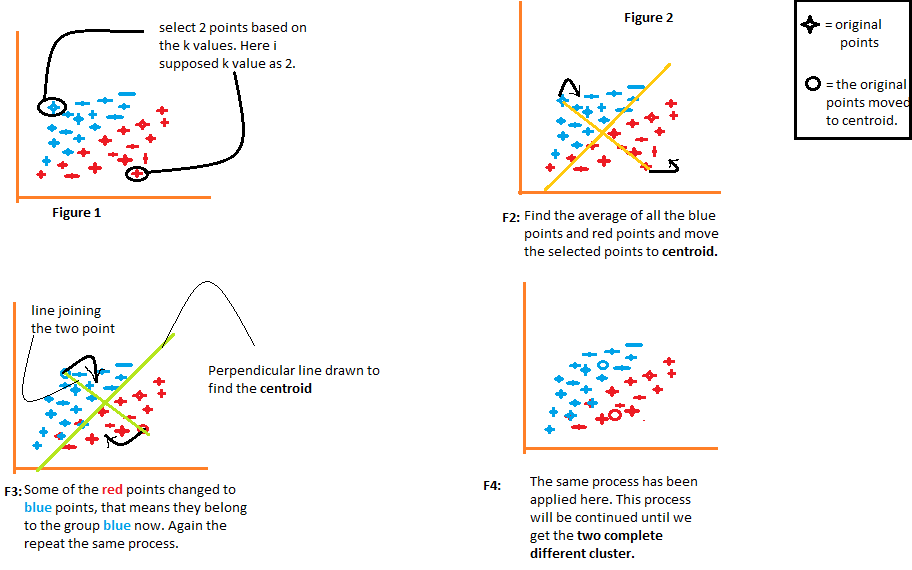
1) El algoritmo elige arbitrariamente el número k de centroides, como se indica en la figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... 1 del siguiente diagrama. Donde k es el número de clústeres que crearía el algoritmo. Digamos que queremos que el algoritmo cree dos grupos a partir de los datos, por lo que estableceremos el valor de k en 2.
2) Luego agrupa los datos en dos partes usando las distancias calculadas de ambos centroides, como se ilustra en la Figura 2. La distancia de cada punto desde ambos centroides se calcula individualmente y posteriormente se agregará al grupo de ese centroide con el que se calcula la distancia. más corto.
El algoritmo también dibuja una línea que une los centroides y una línea perpendicular que intenta agrupar los datos en dos grupos.
3) Una vez que todos los puntos de datos se agrupan en función de sus distancias mínimas desde los centroides correspondientes, el algoritmo calcula la media de cada grupo. Luego se comparan los valores medio y centroide de cada grupo. Si el valor del centroide difiere de la media, entonces el centroide se desplaza al valor medio del grupo. Tanto el centroide «rojo» como el «azul» se reubican en la media del grupo en la figura 3 del siguiente diagrama.
Agrupa los datos una vez más utilizando estos centroides actualizados. Debido al cambio en las posiciones de los centroides, algunos puntos de datos ahora pueden desplazarse en el otro grupo.
4) Nuevamente, calcula la media y la compara con el centroide de los grupos recién generados. Si ambos son diferentes, el centroide se reubicará nuevamente en la media del grupo. Este proceso de calcular la media y compararla con el centroide se repite hasta que los valores del centroide y la media se igualan (valor del centroide = media del grupo). Este es el punto en el que el algoritmo ha segmentado los datos en grupos ‘K’ (2 en este caso).
¿Cómo averiguar cuál es el valor óptimo de k?
El primer paso es proporcionar un valor para k. Cada paso posterior ejecutado por el algoritmo depende completamente del valor de k especificado. Este valor de k ayuda al algoritmo a determinar el número de clústeres que se deben generar. Esto enfatiza la importancia de proporcionar el valor preciso de k. Aquí, se utiliza un método conocido como el «método del codo» para determinar el valor correcto de k. Este es un gráfico de ‘Número de conglomerados K’ frente a «Total dentro de la suma del cuadrado». Los valores discretos de k se grafican en el eje x, mientras que las sumas de cuadrados de los grupos se grafican en el eje y.
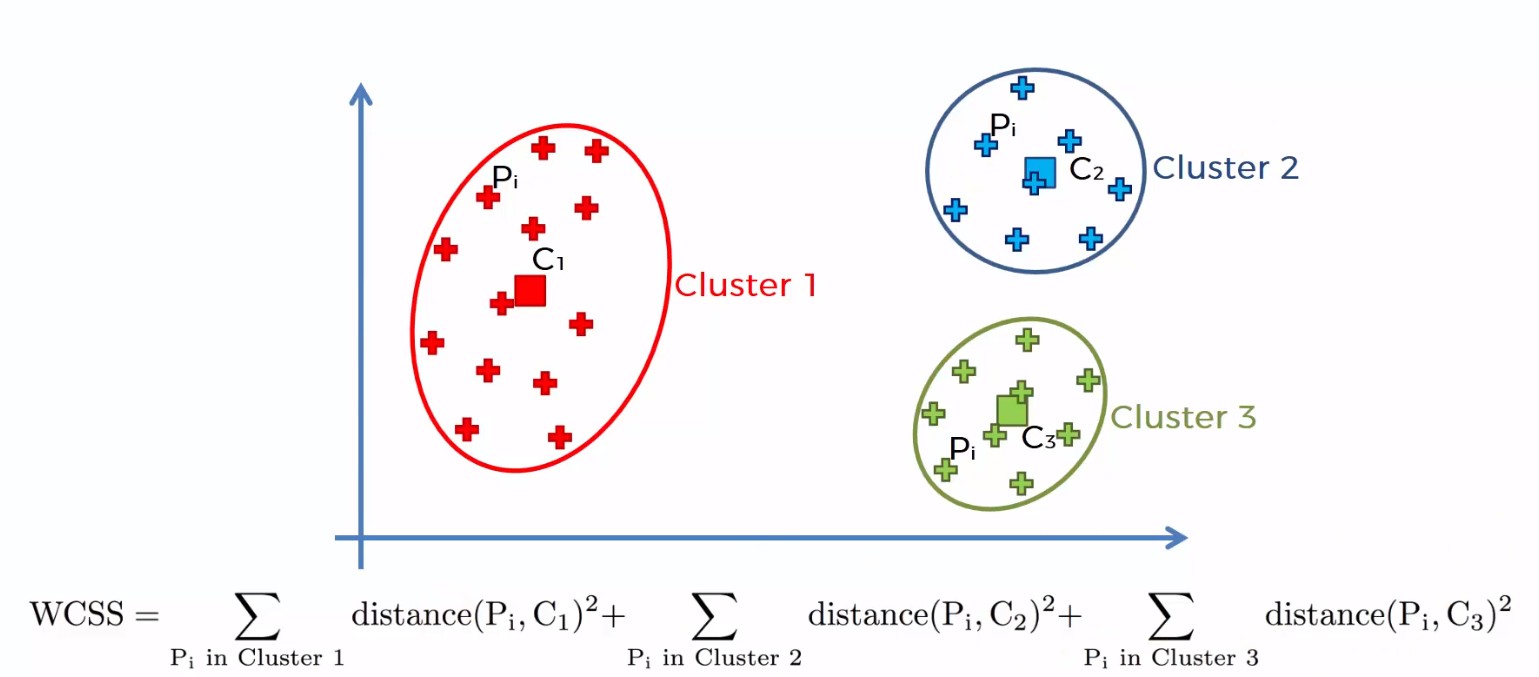
La suma de las distancias al cuadrado entre los puntos individuales y el centroide en cada grupo, seguida de la suma de las distancias al cuadrado para todos los conglomerados, se denomina “Suma de cuadrados dentro del conglomerado”. Podrá comprender esto con la ayuda de los siguientes pasos.
1) Calcule la distancia entre el centroide y cada punto del grupo, eleve al cuadrado y luego sume las distancias al cuadrado para todos los puntos del grupo.
2) Calcula la suma de las distancias al cuadrado de los grupos restantes de la misma manera.
3) Finalmente, sume todas las sumas de grupos para obtener el valor de la “Suma del cuadrado dentro del grupo” como se muestra en la siguiente figura.
El «total dentro de la suma del cuadrado» comienza a disminuir a medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que aumenta el valor de k. La gráfica entre el número de conglomerados y el total dentro de la suma de cuadrados se muestra en la siguiente figura. El número óptimo de conglomerados, o el valor correcto de k, es el punto en el que el valor comienza a disminuir lentamente; esto se conoce como el «punto del codo», y el punto del codo en la siguiente gráfica es k = 4. El «Método del codo» se llama así por la semejanza de la gráfica con el codo, y el punto óptimo para «k» es el punto del codo .
Ventajas de la agrupación en clústeres de k-medias
1) Los datos etiquetados no son obligatorios. Dado que muchos datos del mundo real no están etiquetados, como resultado, se utilizan con frecuencia en una variedad de enunciados de problemas del mundo real.
2) Es fácil de implementar.
3) Puede manejar cantidades masivas de datos.
4) Cuando los datos son grandes, funcionan más rápido que la agrupación jerárquica (para k pequeños).
Desventajas de la agrupación en clústeres de K-medias
1) El valor de K debe seleccionarse manualmente utilizando el «método del codo».
2) La presencia de valores atípicos tendría un impacto adverso en la agrupación. Como resultado, los valores atípicos deben eliminarse antes de utilizar la agrupación de k-medias.
3) Los grupos no se cruzan; un punto solo puede pertenecer a un grupo a la vez. Como resultado de la falta de superposición, ciertos puntos se colocan en grupos incorrectos.
Agrupación de K-medias con R
- Importaremos las siguientes bibliotecas a nuestro trabajo.
biblioteca (intercalación)
biblioteca (ggplot2)
biblioteca (dplyr)
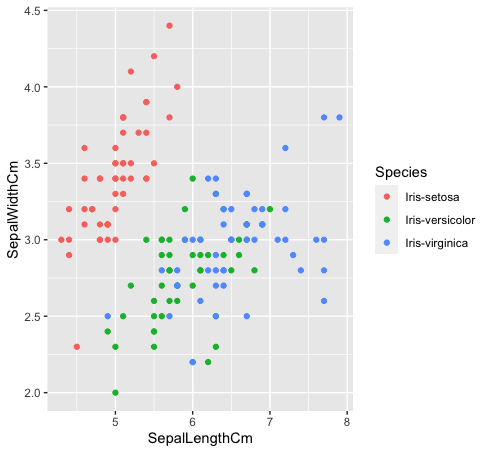
- Trabajaremos con los datos del iris, que contienen tres clases: «Iris-setosa», «Iris-versicolor» e «Iris-virginica».
datos <- read.csv ("iris.csv", encabezado = T)
- Veamos cómo se relacionan estas tres clases entre sí. Las especies «Iris-versicolor» (verde) e «Iris-verginica» (azul) no son linealmente separables. Como se puede ver en el gráfico a continuación, se entremezclan.
datos%>% ggplot (aes (SepalLengthCm, SepalWidthCm, color = Species)) +
geom_point ()
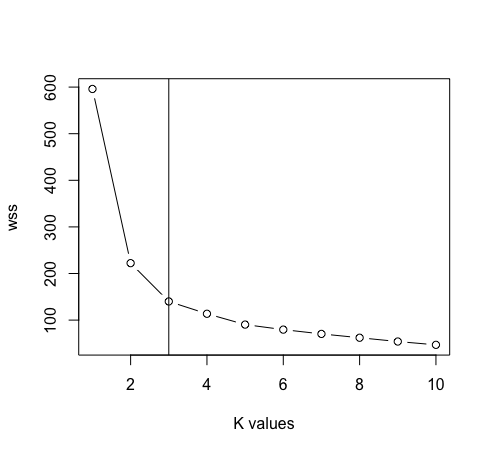
- Después de eliminar la columna de especies de los datos. Ahora usaremos la gráfica del método del codo entre «Suma de cuadrados dentro del conglomerado» y «Valores de k» para determinar el valor adecuado de k. K = 3 es el mejor valor para k en este caso (Nota: hay 3 clases en los datos originales del iris, lo que garantiza la precisión del valor de k).
datos <- datos[, -5]
máximo <- 10
scal <- escala (datos)
wss <- sapply (1: máximo, función (k) {kmeans (scal, k, nstart = 50, iter.max = 15) $ tot.withinss})
plot (1: max, wss, type = «b», xlab = «k valores»)
abline (v = 3)
- Para k = 3, aplique el algoritmo de agrupamientoEl "agrupamiento" es un concepto que se refiere a la organización de elementos o individuos en grupos con características o objetivos comunes. Este proceso se utiliza en diversas disciplinas, incluyendo la psicología, la educación y la biología, para facilitar el análisis y la comprensión de comportamientos o fenómenos. En el ámbito educativo, por ejemplo, el agrupamiento puede mejorar la interacción y el aprendizaje entre los estudiantes al fomentar el trabajo... de K-medias. El enfoque de agrupamiento de K-medias explica el 71,5% de la variabilidad de los datos en este caso.
km <- kmedias (datos[,1:2], k = 3, iter.max = 50)
km
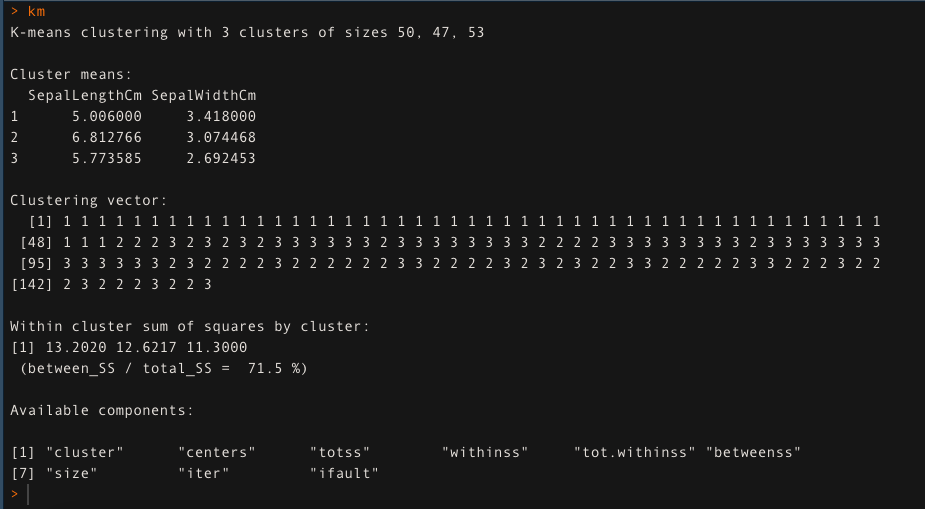
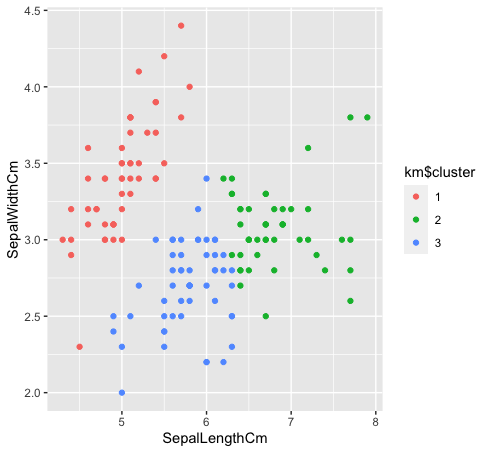
- Veamos cómo se agrupan las tres clases mediante la agrupación en clústeres de k-medias. La agrupación de K-means no creará agrupaciones superpuestas, como todos sabemos. Dado que las especies «verde» y «azul» no son linealmente separables en los datos originales, el agrupamiento de k-medias no pudo capturarlo debido a que tiene grupos reducidos.
km $ cluster <- as.factor (km $ cluster)
datos%>% ggplot (aes (SepalLengthCm, SepalWidthCm, color = km $ cluster)) +
geom_point ()
Un artículo de ~
Shivam Sharma.
Los medios que se muestran en este artículo sobre el algoritmo de agrupación de K-Means no son propiedad de DataPeaker y se utilizan a discreción del autor.
