Agrupación en Python | ¿Qué es K significa Clustering?

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Introducción

El análisis de clústeres o la agrupación en clústeres es un algoritmo de aprendizaje automático no supervisado que agrupa conjuntos de datos sin etiquetar. Su objetivo es formar conglomerados o grupos utilizando los puntos de datos en un conjunto de datos de tal manera que exista una alta similitud entre los conglomerados y una baja similitud entre los conglomerados. En términos simples, la agrupación en clústeres tiene como objetivo formar subconjuntos o grupos dentro de un conjunto de datos que consta de puntos de datos que son realmente similares entre sí y los grupos o subconjuntos o clústeres formados pueden diferenciarse significativamente entre sí.

¿Por qué agrupar?

Supongamos que tenemos un conjunto de datos y no sabemos nada al respecto. Entonces, un algoritmo de agrupamientoEl "agrupamiento" es un concepto que se refiere a la organización de elementos o individuos en grupos con características o objetivos comunes. Este proceso se utiliza en diversas disciplinas, incluyendo la psicología, la educación y la biología, para facilitar el análisis y la comprensión de comportamientos o fenómenos. En el ámbito educativo, por ejemplo, el agrupamiento puede mejorar la interacción y el aprendizaje entre los estudiantes al fomentar el trabajo... puede descubrir grupos de objetos donde las distancias promedio entre los miembros / puntos de datos de cada grupo están más cerca que a los miembros / puntos de datos en otros grupos.

Algunas de las aplicaciones prácticas de Clustering en la vida real como:

1) SegmentaciónLa segmentación es una técnica clave en marketing que consiste en dividir un mercado amplio en grupos más pequeños y homogéneos. Esta práctica permite a las empresas adaptar sus estrategias y mensajes a las características específicas de cada segmento, mejorando así la eficacia de sus campañas. La segmentación puede basarse en criterios demográficos, psicográficos, geográficos o conductuales, facilitando una comunicación más relevante y personalizada con el público objetivo.... de clientes: Encontrar un grupo de clientes con un comportamiento similar dada una gran base de datosUna base de datos es un conjunto organizado de información que permite almacenar, gestionar y recuperar datos de manera eficiente. Utilizadas en diversas aplicaciones, desde sistemas empresariales hasta plataformas en línea, las bases de datos pueden ser relacionales o no relacionales. Su diseño adecuado es fundamental para optimizar el rendimiento y garantizar la integridad de la información, facilitando así la toma de decisiones informadas en diferentes contextos.... de clientes (se da un ejemplo práctico usando la segmentación de clientes bancarios)

2) Clasificación del tráfico de la red: Agrupación de características de las fuentes de tráfico. Los tipos de tráfico se pueden clasificar fácilmente mediante clústeres.

3) Filtro de correo no deseado: Los datos se agrupan en diferentes secciones (encabezado, remitente y contenido) y luego pueden ayudar a clasificar cuáles de ellos son spam.

4)Planificación de la ciudad: Agrupación de casas según su ubicación geográfica, valor y tipo de casa.

Diferentes tipos de algoritmos de agrupación

1) Agrupación de K-medias – Usando este algoritmo, clasificamos un conjunto de datos dado a través de un cierto número de clústeres predeterminados o «k» clústeres.

2) Agrupación jerárquica – Sigue dos enfoques Divisivo y Aglomerativo.

Agglomerative considera cada observación como un solo grupo y luego agrupa puntos de datos similares hasta que se fusionan en un solo grupo y Divisive funciona justo enfrente de él.

3) Fuzzy C significa Clustering – El funcionamiento del algoritmo FCM es casi similar al algoritmo de agrupamiento de k-medias, la principal diferencia es que en FCM un punto de datos se puede colocar en más de un grupo.

4) Agrupación espacial basada en densidad – Útil en las áreas de aplicación donde requerimos estructuras de clústerUn clúster es un conjunto de empresas y organizaciones interconectadas que operan en un mismo sector o área geográfica, y que colaboran para mejorar su competitividad. Estos agrupamientos permiten compartir recursos, conocimientos y tecnologías, fomentando la innovación y el crecimiento económico. Los clústeres pueden abarcar diversas industrias, desde tecnología hasta agricultura, y son fundamentales para el desarrollo regional y la creación de empleo.... no lineales, basadas puramente en la densidad.

Ahora, aquí en este artículo, nos centraremos profundamente en el algoritmo de agrupamiento de k-medias, explicaciones teóricas del funcionamiento de k-medias, ventajas y desventajas, y un problema de agrupamiento práctico resuelto que mejorará la comprensión teórica y le dará una visión adecuada. de cómo funciona la agrupación en clústeres de k-medias.

Qué es k-medio Clustering?

La agrupación de K-Means es un algoritmo de aprendizaje no supervisadoEl aprendizaje no supervisado es una técnica de machine learning que permite a los modelos identificar patrones y estructuras en datos sin etiquetas predefinidas. A través de algoritmos como k-means y análisis de componentes principales, este enfoque se utiliza en diversas aplicaciones, como la segmentación de clientes, la detección de anomalías y la compresión de datos. Su capacidad para revelar información oculta lo convierte en una herramienta valiosa en la..., que se utiliza para agrupar el conjunto de datos sin etiquetar en diferentes grupos / subconjuntos.

Ahora debe estar preguntándose qué significa ‘k’ y ‘significa’ en el k-means Clustering significa ??

Dejando de lado todas sus suposiciones aquí, ‘k’ define el número de grupos predefinidos que deben crearse en el proceso de agrupación, digamos que si k = 2, habrá dos grupos, y para k = 3, habrá tres grupos y así sucesivamente. Como es un algoritmo basado en centroide, ‘medias’ en el agrupamiento de k-medias está relacionado con el centroide de los puntos de datos donde cada grupo está asociado con un centroide. El concepto de un algoritmo basado en centroide se explicará en la explicación de trabajo de k-medias.

Principalmente, el algoritmo de agrupación en clústeres de k-means realiza dos tareas:

• Determina el valor más óptimo para K puntos centrales o centroides mediante un proceso repetitivo.
• Asigna cada punto de datos a su centro k más cercano. El clúster se crea con puntos de datos que están cerca del centro k particular.

¿Cómo funciona la agrupación en clústeres de k-means?

Supongamos que tenemos dos variables X1 y X2, diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada.... a continuación:

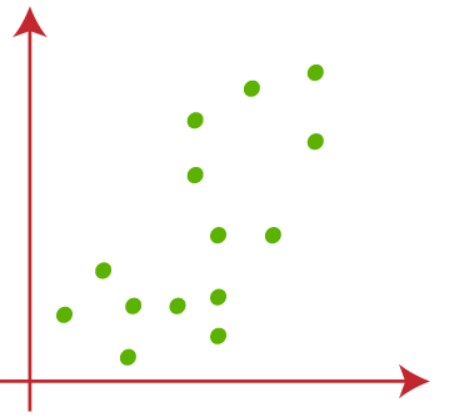
(1) Supongamos que el valor de k, que es el número de grupos predefinidos, es 2 (k = 2), por lo que aquí agruparemos nuestros datos en 2 grupos.

Es necesario elegir k puntos aleatorios para formar los grupos. No pueden existir restricciones en la selección de k puntos aleatorios desde el interior de los datos ni desde el exterior. Entonces, aquí estamos considerando 2 puntos como k puntos (que no forman parte de nuestro conjunto de datos) que se muestran en la siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas....:

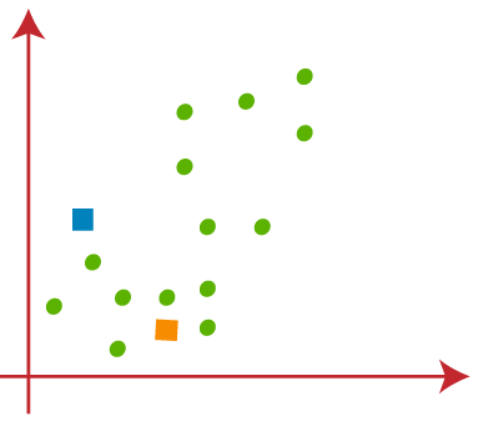
(2) El siguiente paso es asignar cada punto de datos del conjunto de datos en el diagrama de dispersión a su punto k más cercano, esto se hará calculando la distancia euclidiana entre cada punto con un punto k y dibujando una medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... entre ambos centroides, que se muestra en la figura a continuación-

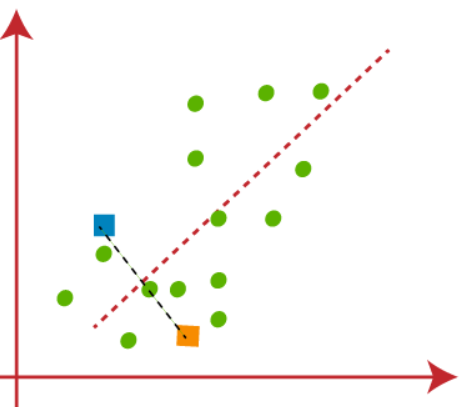
Podemos observar claramente que el punto a la izquierda de la línea roja está cerca de K1 o el centroide azul y los puntos a la derecha de la línea roja están cerca de K2 o el centroide naranja.

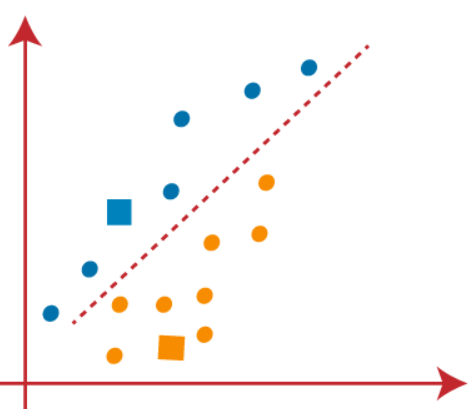
(3) Como necesitamos encontrar el punto más cercano, repetiremos el proceso eligiendo un nuevo centroide. Para elegir los nuevos centroides, calcularemos el centro de gravedad de estos centroides y encontraremos nuevos centroides como se muestra a continuación:

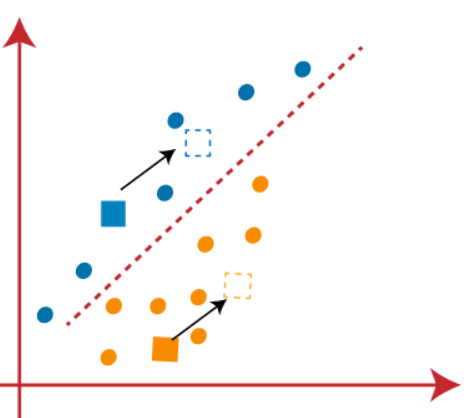
(4) Ahora, necesitamos reasignar cada punto de datos a un nuevo centroide. Para ello, tenemos que repetir el mismo proceso de encontrar una línea mediana. La mediana será como a continuación:

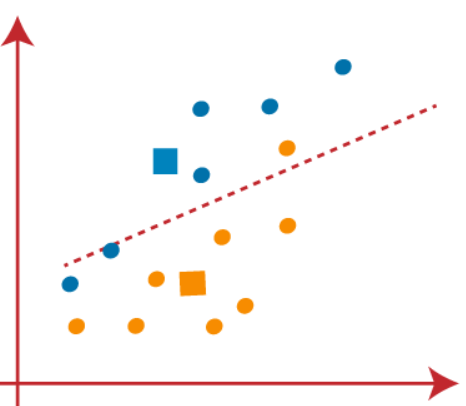
En la imagen de arriba, podemos ver, un punto naranja está en el lado izquierdo de la línea y dos puntos azules están justo a la línea. Entonces, estos tres puntos se asignarán a nuevos centroides

Seguiremos encontrando nuevos centroides hasta que no haya puntos diferentes en ambos lados de la línea.

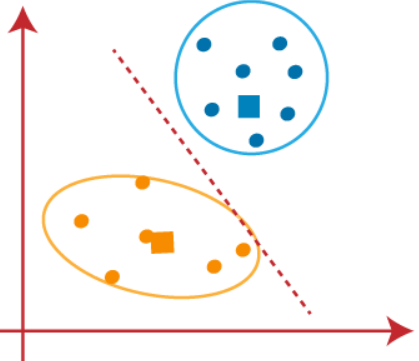
Ahora podemos eliminar los centroides asumidos, y los dos grupos finales serán como se muestra en la imagen de abajo

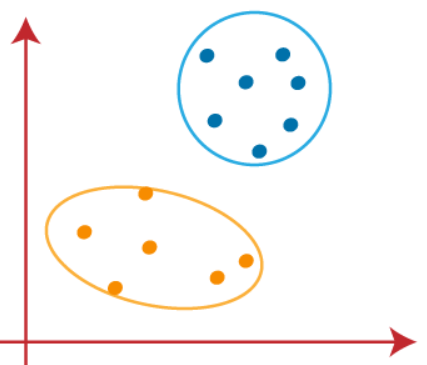
Hasta ahora hemos visto cómo funciona el algoritmo de k-medias y los distintos pasos involucrados para llegar al destino final de los clusters diferenciadores.

Ahora todos deben estar preguntándose cómo elegir el valor de k número de clusters.

El rendimiento del algoritmo de agrupación de K-means depende en gran medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de las agrupaciones que forma. Elegir el número óptimo de clústeres es una tarea difícil. Hay varias formas de encontrar el número óptimo de conglomerados, pero aquí estamos discutiendo dos métodos para encontrar el número de conglomerados o el valor de K que es el Método del codo y puntuación de la silueta.

Método del codo para encontrar ‘k’ número de grupos:[1]

El método Elbow es el más popular para encontrar un número óptimo de conglomerados, este método utiliza WCSS (Suma de cuadrados dentro de los conglomerados) que representa las variaciones totales dentro de un conglomerado.

WCSS = ∑_{Pi en Cluster1} distancia (P_I C₁)² + ∑_{Pi en Cluster2}distancia (P_I C₂)²+ ∑_{Pi en CLuster3} distancia (P_I C₃)²

En la fórmula anterior ∑_{Pi en Cluster1} distancia (P_I C₁)² es la suma del cuadrado de las distancias entre cada punto de datos y su centroide dentro de un grupo1 de manera similar para los otros dos términos en la fórmula anterior.

Pasos involucrados en el método del codo:

• K- significa que el agrupamiento se realiza para diferentes valores de k (de 1 a 10).
• WCSS se calcula para cada grupo.
• Se traza una curva entre los valores WCSS y el número de conglomerados k.
• El punto de curvatura agudo o un punto de la trama parece un brazo, entonces ese punto se considera como el mejor valor de K.

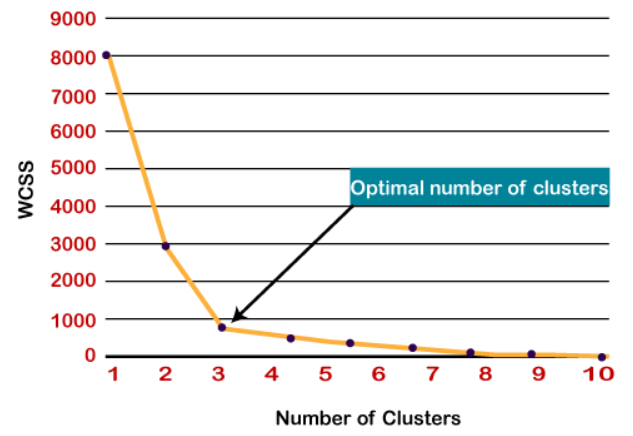
Así que aquí, como podemos ver, una curva pronunciada está en k = 3, por lo que el número óptimo de grupos es 3.

Puntuación de silueta Método para encontrar ‘k’ número de conglomerados

El valor de silueta es una medida de cuán similar es un objeto a su propio grupo (cohesión) en comparación con otros grupos (separación). La silueta varía de -1 a +1, donde un valor alto indica que el objeto se corresponde bien con su propio grupo y no con los grupos vecinos. Si la mayoría de los objetos tienen un valor alto, entonces la configuración de agrupamiento es apropiada. Si muchos puntos tienen un valor bajo o negativo, entonces la configuración de la agrupación en clústeres puede tener demasiados o muy pocos clústeres.

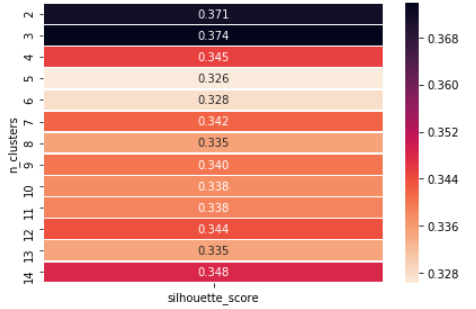
Ejemplo que muestra cómo podemos elegir el valor de ‘k’, ya que podemos ver que en n = 3 tenemos la puntuación máxima de silueta, por lo tanto, elegimos el valor de k = 3.

Ventajas de utilizar la agrupación en clústeres de k-means

• Fácil de implementar.
• Con una gran cantidad de variables, K-Means puede ser computacionalmente más rápido que el agrupamiento jerárquico (si K es pequeño).
• Las k-medias pueden producir agrupaciones más altas que las agrupaciones jerárquicas.

Desventajas de usar clustering de k-means

Es difícil predecir el número de agrupaciones (valor K).

Las semillas iniciales tienen un fuerte impacto en los resultados finales.

Implementación práctica del algoritmo de agrupación en clústeres K-means utilizando Python (segmentación de clientes bancarios)

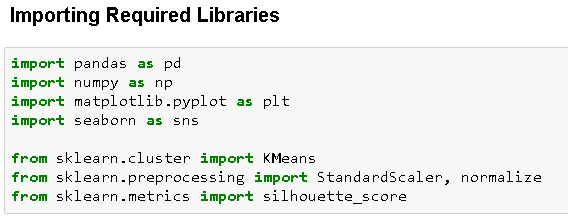
Aquí estamos importando las bibliotecas necesarias para nuestro análisis.

Leer los datos y obtener las 5 mejores observaciones para echar un vistazo al conjunto de datos

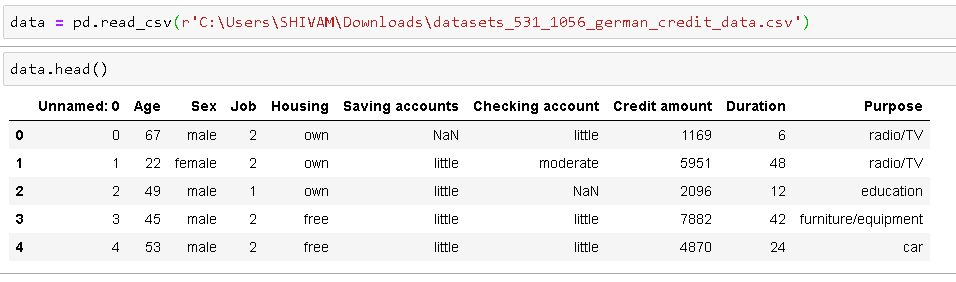
No se ha incluido el código para EDA (Análisis de datos exploratorios), se realizó EDA con estos datos y se realizó un análisis de valores atípicos para limpiar los datos y hacerlos aptos para nuestro análisis.

Como sabemos, las K-medias se realizan solo en los datos numéricos, por lo que elegimos las columnas numéricas para nuestro análisis.

Ahora, para realizar la agrupación de k-medias como se discutió anteriormente en este artículo, necesitamos encontrar el valor del número ‘k’ de agrupaciones y podemos hacerlo usando el siguiente código, aquí usamos varios valores de k para la agrupación y luego seleccionando utilizando el Método del codo.

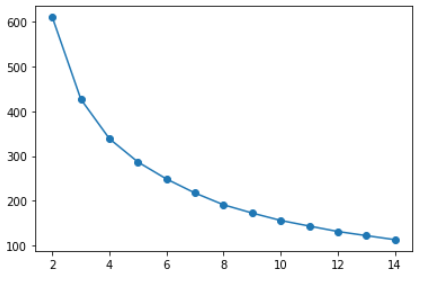
A medida que aumenta el número de conglomerados, la varianza (suma de cuadrados dentro del conglomerado) disminuye. El codo en 3 o 4 grupos representa el equilibrio más parsimonioso entre minimizar el número de grupos y minimizar la varianza dentro de cada grupo, por lo que podemos elegir un valor de k para que sea 3 o 4

Ahora se muestra cómo podemos usar el método del valor de silueta para encontrar el valor de ‘k’.

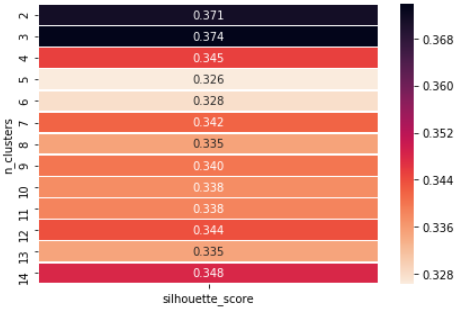
Si observamos, obtenemos el número óptimo de conglomerados en n = 3, por lo que finalmente podemos elegir el valor de k = 3.

Ahora, ajustar el algoritmo de k significa usando el valor de k = 3 y trazar el mapa de calorUn "mapa de calor" es una representación gráfica que utiliza colores para mostrar la densidad de datos en un área específica. Comúnmente utilizado en análisis de datos, marketing y estudios de comportamiento, este tipo de visualización permite identificar patrones y tendencias rápidamente. A través de variaciones cromáticas, los mapas de calor facilitan la interpretación de grandes volúmenes de información, ayudando a la toma de decisiones informadas.... para los clústeres.

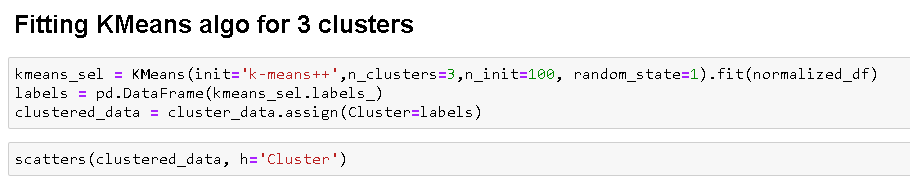
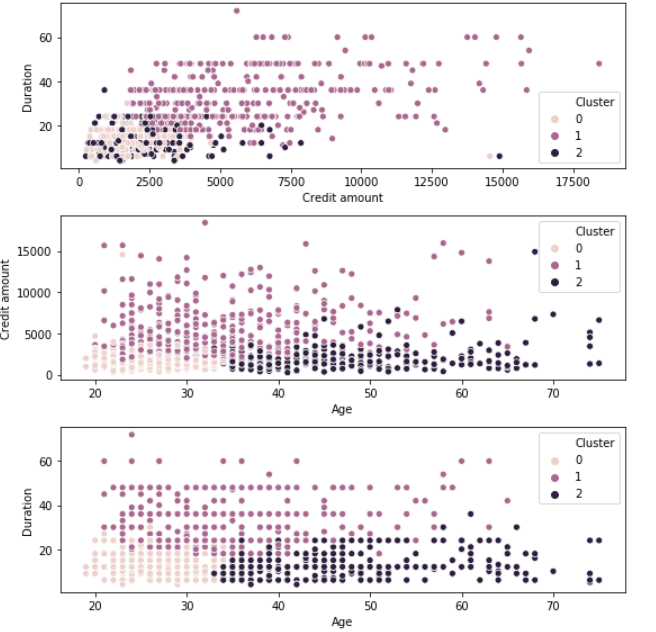
Análisis final

Clúster 0: clientes jóvenes que obtienen préstamos de bajo crédito durante un período breve

Grupo 1: Clientes de mediana edad que obtienen préstamos de alto crédito durante un período prolongado

Grupo 2: Clientes de edad avanzada que obtienen préstamos de crédito medio por un período corto

Conclusión

Hemos discutido qué es la agrupación en clústeres, sus tipos y su aplicación en diferentes industrias. Discutimos qué es la agrupación de k-medias, el funcionamiento del algoritmo de agrupación de k-medias, dos métodos para seleccionar el número ‘k’ de agrupaciones, y sus ventajas y desventajas. Luego, pasamos por la implementación práctica del algoritmo de agrupación en clústeres de k-medias utilizando el problema de segmentación de clientes bancarios en Python.

Referencias:

(1) img (1) a img (8) y [1] , referencia tomada del «Algoritmo de agrupación en clústeres de K-medias»

https://www.javatpoint.com/k-means-clustering-algorithm-in-machine-learning

Relacionado