En el último post (haga clic aquí), hablamos brevemente sobre los conceptos básicos de la técnica ANN. Pero antes de utilizar la técnica, un analista debe saber, ¿cómo funciona verdaderamente la técnica? Aún cuando no se requiera la derivación detallada, se debe conocer el marco del algoritmo. Este conocimiento sirve para múltiples propósitos:
- En primer lugar, nos ayuda a comprender el impacto de incrementar / reducir el conjunto de datos vertical u horizontalmente en el tiempo computacional.
- En segundo lugar, nos ayuda a comprender las situaciones o casos en los que el modelo encaja mejor.
- En tercer lugar, además nos ayuda a explicar por qué determinado modelo funciona mejor en determinados entornos o situaciones.
Este post le proporcionará una comprensión básica del marco de la red neuronal artificial (ANN). No entraremos en la derivación real, pero la información proporcionada en este post será suficiente para que pueda apreciar e poner en práctica el algoritmo. Al final del post, además presentaré mis puntos de vista sobre los tres propósitos básicos de la comprensión de cualquier algoritmo mencionado previamente.
Formulación de red neuronal
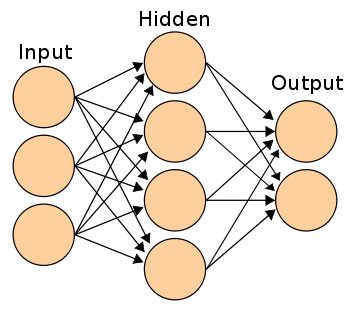
Comenzaremos con la comprensión de la formulación de una red neuronal de capa oculta simple. Se puede representar una red neuronal simple como se muestra en la próxima figura:
Los vínculos entre los nodos son el hallazgo más crucial en una RNA. Volveremos a “cómo hallar el peso de cada vínculo” después de discutir el marco general. Los únicos valores conocidos en el diagrama anterior son las entradas. Llamemos a las entradas como I1, I2 e I3, los estados ocultos como H1, H2.H3 y H4, las salidas como O1 y O2. Los pesos de los vínculos se pueden denotar con la próxima notación:
W (I1H1) es el peso del link entre los nodos I1 y H1.
A continuación se muestra el marco en el que funcionan las redes neuronales artificiales (ANN):
Pocos detalles estadísticos sobre el marco
Cada cálculo de vinculación en una red neuronal artificial (ANN) es equivalente. En general, asumimos una vinculación sigmoidea entre las variables de entrada y la tasa de activación de los nodos ocultos o entre los nodos ocultos y la tasa de activación de los nodos de salida. Preparemos la ecuación para hallar la tasa de activación de H1.
Logit (H1) = W (I1H1) * I1 + W (I2H1) * I2 + W (I3H1) * I3 + Constante = f
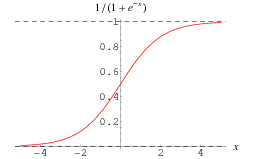
=> P (H1) = 1 / (1 + e ^ (- f))
A continuación se muestra cómo se ve la vinculación sigmoidea:
¿Cómo se recalibran las pesas? Una nota corta
La recalibración de pesos es un procedimiento fácil, pero largo. Los únicos nodos donde conocemos la tasa de error son los nodos de salida. La recalibración de pesos en el vínculo entre el nodo oculto y el nodo de salida es una función de esta tasa de error en los nodos de salida. Pero, ¿cómo encontramos la tasa de error en los nodos ocultos? Se puede demostrar estadísticamente que:
Error @ H1 = W (H1O1) *[email protected] + W (H1O2) *[email protected]
Usando estos errores, podemos volver a calibrar los pesos de link entre los nodos ocultos y los nodos de entrada de una manera equivalente. Imagine que este cálculo se realiza varias veces para cada una de las observaciones del conjunto de entrenamiento.
Las tres preguntas básicas
¿Cuál es la correlación entre el tiempo consumido por el algoritmo y el volumen de datos (en comparación con modelos tradicionales como el logístico)?
Como se mencionó previamente, para cada observación, ANN realiza múltiples recalibraciones para cada peso de link. Por eso, el tiempo que tarda el algoritmo aumenta mucho más rápido que otros algoritmos tradicionales para el mismo aumento en el volumen de datos.
¿En qué situación encaja mejor el algoritmo?
ANN rara vez se utiliza para el modelado predictivo. El motivo es que las Redes Neuronales Artificiales (ANN) por lo general intentan encajar demasiado la vinculación. ANN se utiliza de forma general en los casos en que lo que ha sucedido en el pasado se repite casi exactamente de la misma manera. A modo de ejemplo, digamos que estamos jugando el juego de Black Jack contra una computadora. Un oponente inteligente basado en ANN sería un oponente muy bueno para este caso (suponiendo que puedan mantener el tiempo de cálculo bajo). Con el tiempo, ANN se preparará para todos los casos posibles de flujo de tarjetas. Y dado que no estamos barajando cartas con un crupier, ANN podrá memorizar cada llamada. Por eso, es una especie de técnica de aprendizaje automático que dispone de una memoria enorme. Pero no funciona bien en el caso de que la población de puntuación sea significativamente distinto en comparación con la muestra de entrenamiento. A modo de ejemplo, si planeo dirigirme a un cliente para una campaña usando su respuesta anterior de una ANN. Probablemente utilizaré una técnica incorrecta, dado que podría haber ajustado demasiado la vinculación entre la solución y otros predictores.
Por la misma razón, funciona muy bien en casos de acreditación de imágenes y acreditación de voz.
¿Qué hace que ANN sea un modelo muy sólido en lo que respecta a la memorización?
Las redes neuronales artificiales (ANN) disponen muchos coeficientes diferentes, que puede aprovechar al máximo. Por eso, puede manejar mucha más variabilidad en comparación con los modelos tradicionales.
¿Le fue útil el post? ¿Ha utilizado alguna otra herramienta de aprendizaje automático recientemente? ¿Planea usar ANN en alguno de sus problemas comerciales? En caso de ser así, cuéntenos cómo planea hacerlo.