En Machine Learning, utilizamos varios tipos de algoritmos para permitir que las máquinas aprendan las relaciones dentro de los datos proporcionados y hagan predicciones basadas en patrones o reglas identificadas en el conjunto de datos. Entonces, la regresión es una técnica de aprendizaje automático donde el modelo predice la salida como un valor numérico continuo.
Fuente: https://www.hindish.com
El análisis de regresión se usa a menudo en finanzas, inversiones y otros, y descubre la relación entre una sola variable dependiente (variable objetivo) que depende de varias independientes. Por ejemplo, predecir el precio de la vivienda, el mercado de valores o el salario de un empleado, etc.son los más comunes
problemas de regresión.
Los algoritmos que vamos a cubrir son:
1. Regresión lineal
2. Árbol de decisiones
3. Regresión de vectores de apoyo
4. Regresión de lazo
5. Bosque aleatorio
1. Regresión lineal
La regresión lineal es un algoritmo de aprendizaje automático que se utiliza para el aprendizaje supervisado. La regresión lineal realiza la tarea de predecir una variable dependiente (objetivo) en función de las variables independientes dadas. Entonces, esta técnica de regresión encuentra una relación lineal entre una variable dependiente y las otras variables independientes dadas. Por lo tanto, el nombre de este algoritmo es Regresión lineal.
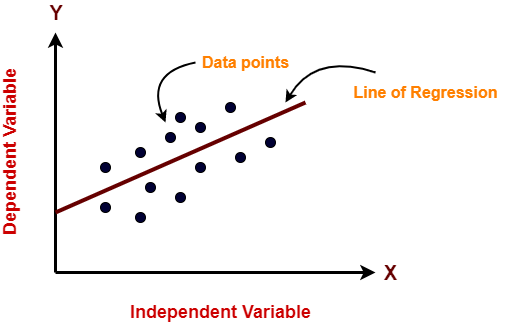
En la figura anterior, en el eje X está la variable independiente y en el eje Y está la salida. La línea de regresión es la línea que mejor se ajusta a un modelo. Y nuestro principal objetivo en este algoritmo es encontrar la línea que mejor se ajuste.
Pros:
- La regresión lineal es sencilla de implementar.
- Menor complejidad en comparación con otros algoritmos.
- La regresión lineal puede provocar un ajuste excesivo, pero se puede evitar utilizando algunas técnicas de reducción de dimensionalidad, técnicas de regularización y validación cruzada.
Contras:
- Los valores atípicos afectan gravemente a este algoritmo.
- Simplifica demasiado los problemas del mundo real al asumir una relación lineal entre las variables, por lo que no se recomienda para casos de uso prácticos.
Implementación
import numpy as np from sklearn.linear_model import LinearRegression X = np.array([[2, 1], [3, 2], [4, 2], [5, 3]]) # y = 1 * x_0 + 2 * x_1 + 3 y = np.dot(X, np.array([1, 2])) + 3 lr = LinearRegression().fit(X, y) lr.predict(np.array([[1, 5]])) Output array([14.])
2. Árbol de decisiones
Los modelos de árbol de decisión se pueden aplicar a todos aquellos datos que contienen características numéricas y características categóricas. Los árboles de decisión son buenos para capturar la interacción no lineal entre las características y la variable de destino. Los árboles de decisión coinciden en cierto modo con el pensamiento a nivel humano, por lo que es muy intuitivo comprender los datos.
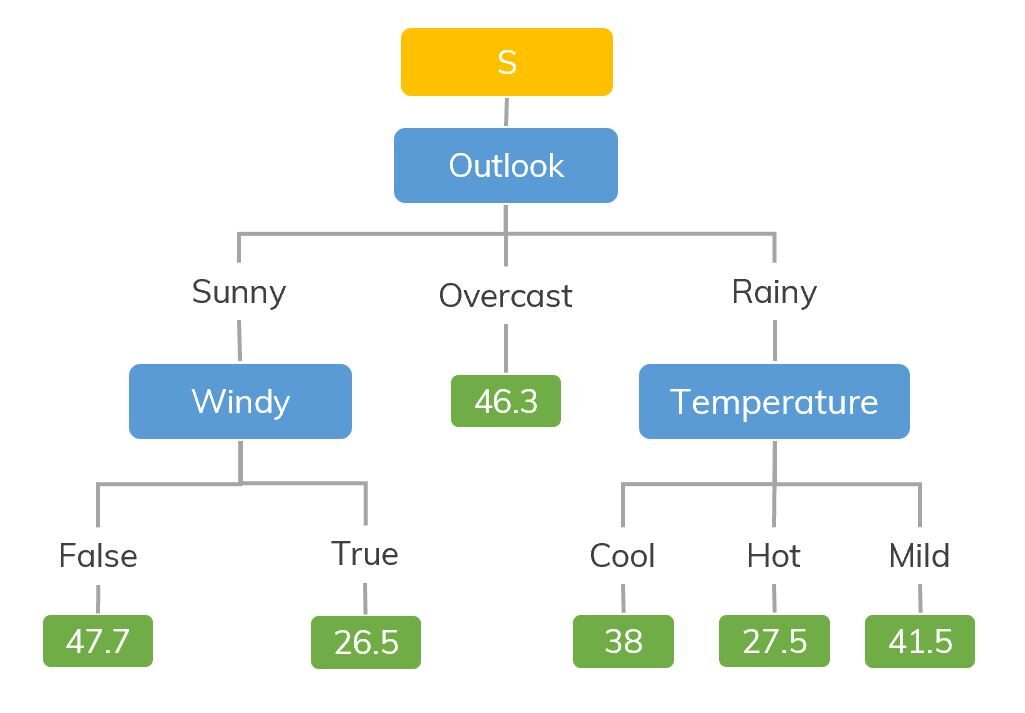
Fuente: https://dinhanhthi.com
Por ejemplo, si estamos clasificando cuántas horas juega un niño en un clima en particular, el árbol de decisiones se parece un poco a esto en la imagen.
Entonces, en resumen, un árbol de decisiones es un árbol donde cada nodo representa una característica, cada rama representa una decisión y cada hoja representa un resultado (valor numérico para la regresión).
Pros:
- Fácil de entender e interpretar, visualmente intuitivo.
- Puede trabajar con características numéricas y categóricas.
- Requiere poco procesamiento previo de datos: sin necesidad de codificación one-hot, variables ficticias, etc.
Contras:
- Tiende a sobreajustarse.
- Un pequeño cambio en los datos tiende a provocar una gran diferencia en la estructura del árbol, lo que provoca inestabilidad.
Implementación
import numpy as np from sklearn.tree import DecisionTreeRegressor rng = np.random.RandomState(1) X = np.sort(5 * rng.rand(80, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - rng.rand(16)) # Fit regression model regr = DecisionTreeRegressor(max_depth=2) regr.fit(X, y) # Predict X_test = np.arange(0.0, 5.0, 1)[:, np.newaxis] result = regr.predict(X_test) print(result) Output: [ 0.05236068 0.71382568 0.71382568 0.71382568 -0.86864256]
3. Regresión de vectores de apoyo
Debe haber oído hablar de SVM, es decir, Support Vector Machine. SVR también usa la misma idea de SVM pero aquí intenta predecir los valores reales. Este algoritmo utiliza hiperplanos para segregar los datos. En caso de que esta separación no sea posible, entonces usa el truco del kernel donde la dimensión aumenta y luego los puntos de datos se vuelven separables por un hiperplano.
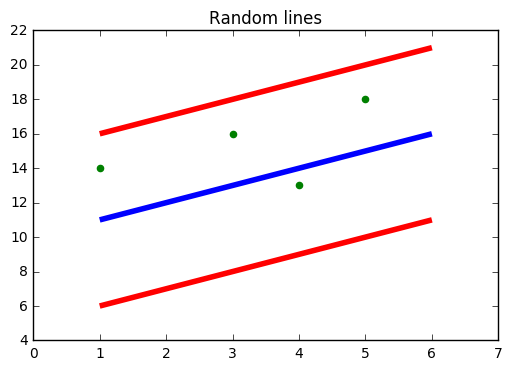
Fuente: https://www.medium.com
En la figura de arriba, la línea azul es el hiperplano; La línea roja es la línea límite
Todos los puntos de datos están dentro de la línea de límite (línea roja). El principal objetivo de SVR es básicamente considerar los puntos que se encuentran dentro de la línea de límite.
Pros:
- Robusto a valores atípicos.
- Excelente capacidad de generalización
- Alta precisión de predicción.
Contras:
- No apto para grandes conjuntos de datos.
- No funcionan muy bien cuando el conjunto de datos tiene más ruido.
Implementación
from sklearn.svm import SVR import numpy as np rng = np.random.RandomState(1) X = np.sort(5 * rng.rand(80, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - rng.rand(16)) # Fit regression model svr = SVR().fit(X, y) # Predict X_test = np.arange(0.0, 5.0, 1)[:, np.newaxis] svr.predict(X_test)
Output: array([-0.07840308, 0.78077042, 0.81326895, 0.08638149, -0.6928019 ])
4. Regresión de lazo
- LASSO son las siglas de Operador de contracción de selección mínima absoluta. La contracción se define básicamente como una restricción de atributos o parámetros.
- El algoritmo funciona encontrando y aplicando una restricción a los atributos del modelo que provocan que los coeficientes de regresión de algunas variables se reduzcan a cero.
- Las variables con un coeficiente de regresión de cero se excluyen del modelo.
- Por lo tanto, el análisis de regresión de lazo es básicamente un método de selección de variables y contracción y ayuda a determinar cuáles de los predictores son más importantes.
Pros:
Contras:
- LASSO seleccionará solo una característica de un grupo de características correlacionadas
- Las características seleccionadas pueden estar muy sesgadas.
Implementación
from sklearn import linear_model import numpy as np rng = np.random.RandomState(1) X = np.sort(5 * rng.rand(80, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - rng.rand(16)) # Fit regression model lassoReg = linear_model.Lasso(alpha=0.1) lassoReg.fit(X,y) # Predict X_test = np.arange(0.0, 5.0, 1)[:, np.newaxis] lassoReg.predict(X_test)
Output: array([ 0.78305084, 0.49957596, 0.21610108, -0.0673738 , -0.35084868])
5. Regresor de bosque aleatorio
Los bosques aleatorios son un conjunto (combinación) de árboles de decisión. Es un algoritmo de aprendizaje supervisado que se utiliza para clasificación y regresión. Los datos de entrada se pasan a través de múltiples árboles de decisión. Se ejecuta construyendo un número diferente de árboles de decisión en el momento del entrenamiento y generando la clase que es el modo de las clases (para clasificación) o predicción media (para regresión) de los árboles individuales.
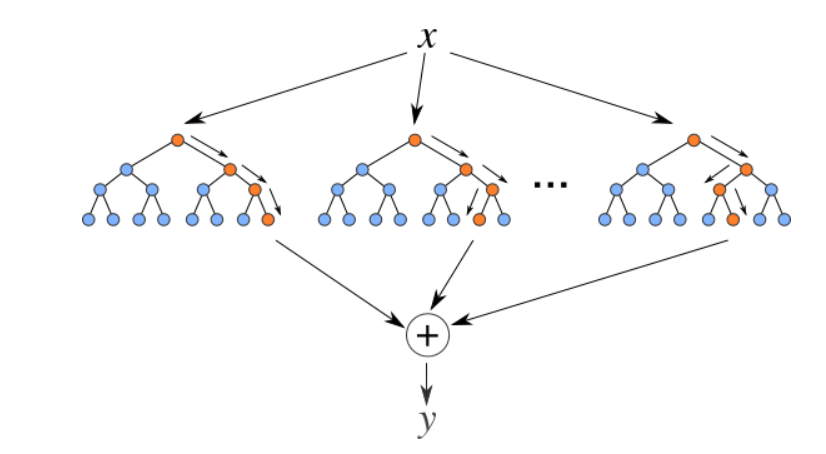
Fuente: https://levelup.gitconnected.com
Pros:
- Bueno para aprender relaciones complejas y no lineales
- Muy fácil de interpretar y comprender.
Contras:
- Son propensos a sobreajustarse
- El uso de conjuntos de bosques aleatorios más grandes para lograr un mayor rendimiento ralentiza su velocidad y luego también necesitan más memoria.
Implementación
from sklearn.ensemble import RandomForestRegressor from sklearn.datasets import make_regression X, y = make_regression(n_features=4, n_informative=2, random_state=0, shuffle=False) rfr = RandomForestRegressor(max_depth=3) rfr.fit(X, y) print(rfr.predict([[0, 1, 0, 1]])) Output: [33.2470716]
Notas finales
Estos son algunos algoritmos de regresión populares, hay muchos más y también algoritmos avanzados. Explórelos también. También puede seguir estos algoritmos de clasificación para aumentar su conocimiento de aprendizaje automático.
Gracias por leer si llegaste aquí 🙂
Vamos a conectarnos LinkedIn
Los medios que se muestran en este artículo no son propiedad de Analytics Vidhya y se utilizan a discreción del autor.






