Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
¿Cuántos datos son suficientes para establecer la significación estadística? En otras palabras, ¿cuál debería ser el tamaño de muestra óptimo? A menudo, no es del todo factible realizar el experimento estadístico varias veces para garantizar suficiente potencia. Al mismo tiempo, nuestro modelo de aprendizaje automático podría no ser estadísticamente concluyente si no tenemos un tamaño de muestra adecuado.
Primero analicemos el poder estadístico en detalle.
El poder estadístico de una prueba de hipótesis implica la probabilidad de detectar un efecto, dado que existe un efecto verdadero. Es la confianza que se deriva de los resultados de un estudio y está inversamente relacionada con el error tipo 2.
Tenga en cuenta que el error de tipo 2 es falso negativo cuando no rechazamos las hipótesis nulas falsas.
En este punto, es importante entender ¿qué es la hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos....? Es una prueba de hipótesis estadística que asume un resultado. Por ejemplo, la hipótesis nula en el estadístico KS implica que las dos poblaciones pertenecen a una distribución similar.

Fuente: Wiki con adiciones del autor
Es importante observar en la ilustración anterior que cuanto mayor es la potencia de una prueba, menor es el β, es decir, el error de tipo 2
Como la potencia estadística más baja de un experimento conduce a conclusiones no válidas sobre el resultado, se desea que los experimentos tengan un umbral mínimo de potencia. Generalmente, se espera que sea del 80% o más. Una potencia del 80% significa que hay un 80% de probabilidad de detectar un efecto que existe (y, a su vez, un 20% de probabilidad de observar un error de tipo 2).
Análisis de poder:
Ahora es el momento de ver una imagen más amplia, es decir, el análisis de potencia que depende de cuatro variables relacionadas, como se menciona a continuación:
1) Tamaño del efecto: cuanto más prominente tienen los datos, menor es el error aleatorio.
2) Tamaño de la muestra: un tamaño de muestra más grande ayuda a detectar efectos más pequeños
3) Nivel de significación: α
4) Poder estadístico
Las cuatro variables están vinculadas entre sí y el cambio de una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... afecta al resto de las variables.
El análisis de potencia es el proceso de estimar una de las 4 variables dadas valores para las 3 variables. Suele utilizarse para estimar el tamaño mínimo de muestra para realizar un experimento.
A medida que aumentamos el tamaño de la muestra, también podemos detectar los pequeños efectos, aunque a costa de realizar experimentos estadísticos varias veces. Incluso entonces, llega un punto en el que agregar más datos no aumenta más la potencia.
Tenga en cuenta que es muy posible que la muestra con la que estamos trabajando no capture el efecto incluso si existe en la población. Esto se atribuye en gran parte al error de muestreo cuando la muestra no es representativa de la población.
El análisis de potencia también se utiliza para verificar y validar los resultados y hallazgos del experimento. Por ejemplo, si especificamos el tamaño del efecto, el tamaño de la muestra y el nivel de significancia, podemos calcular la potencia de un experimento para verificar si la probabilidad de error de tipo 2 está dentro de un rango aceptable.
Según documentación, podemos resolver cualquiera de los 4 parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... en una prueba T independiente de 2 muestras:

Fuente: Autor
También podemos usar trazar curvas de potencia para comprobar cómo la variación del tamaño del efecto y el tamaño de la muestra diferente cambia la potencia del experimento a un nivel de significancia dado.
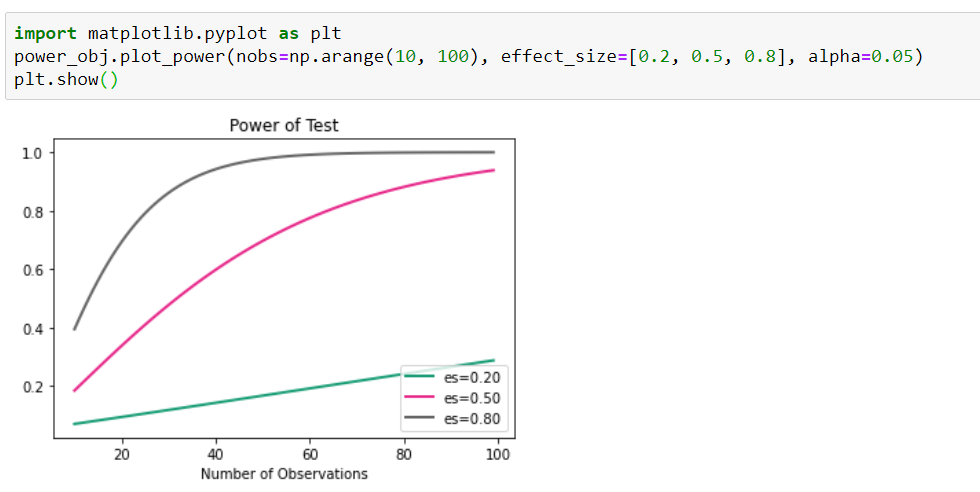
Fuente: Autor
Referencias:
https://statisticsbyjim.com/hypothesis-testing/sample-size-power-analysis/
https://machinelearningmastery.com/statistical-power-and-power-analysis-in-python/
Relacionado
Posts Relacionados:
- Estadísticas para la ciencia de datos | Guía para principiantes de estadísticas para ciencia de datos
- Estadísticas para la ciencia de datos | Comprensión de las estadísticas
- Estadísticas en Excel | 10 funciones estadísticas en Microsoft Excel
- Pruebas estadísticas | Selección de características mediante pruebas estadísticas






