Aprendizaje automático con Python: regresión logística

¿Qué es la regresión logística?

Este artículo asume que posee conocimientos básicos y comprensión de los conceptos de aprendizaje automático, como el vector de destino, la matriz de características y términos relacionados.

Regresión logística: probablemente uno de los algoritmos de aprendizaje automático supervisado más interesantes en el aprendizaje automático. A pesar de tener «Regresión» en su nombre, Regresión logística es un método supervisado de uso popular. Clasificación Algoritmo. Regresión logística, junto con sus primos relacionados a saber. Regresión logística multinomial, nos otorga la capacidad de predecir si una observación pertenece a una determinada clase utilizando un enfoque que es sencillo, fácil de entender y sigue.

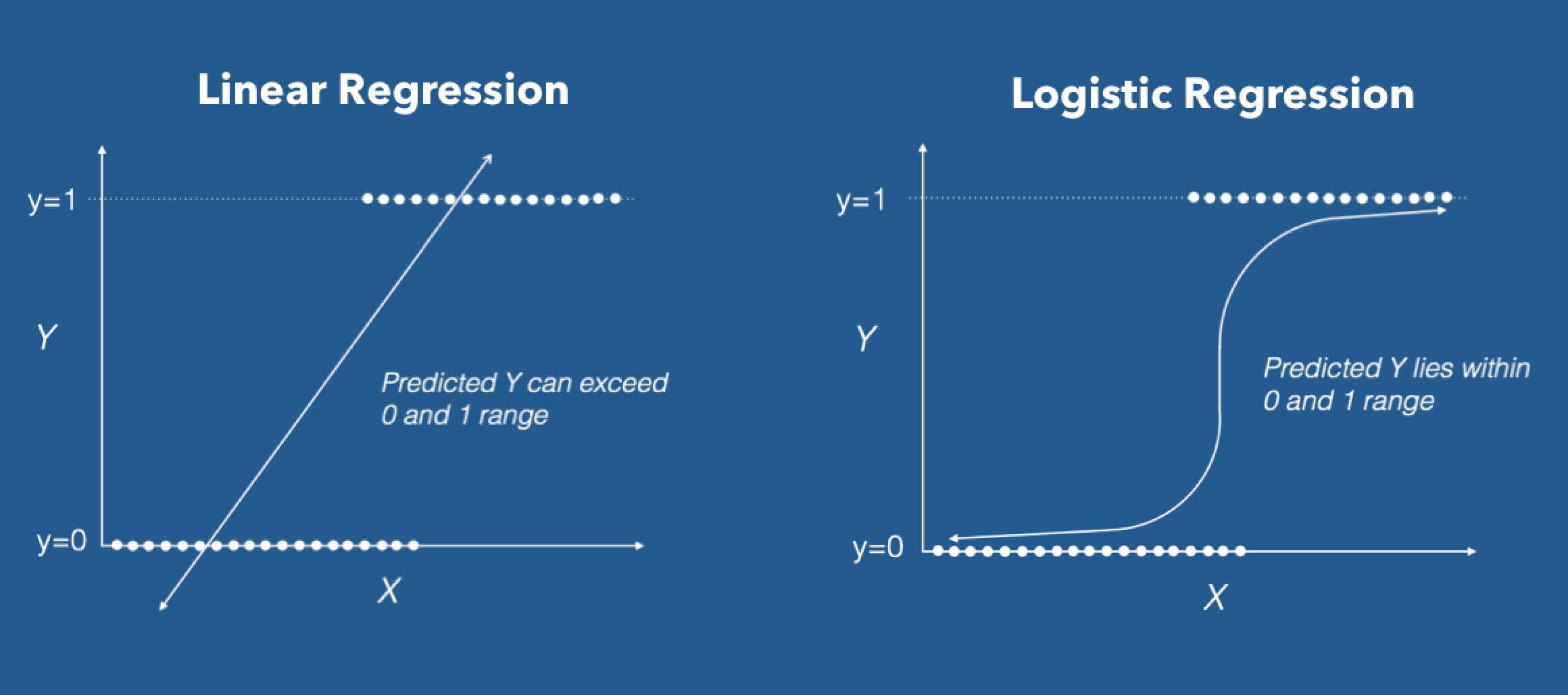
Fuente: DZone

Regresión logística en su forma base (por defecto) es un Clasificador binario. Esto significa que el vector objetivo solo puede tomar la forma de uno de dos valores. En la fórmula del algoritmo de regresión logística, tenemos un modelo lineal, por ejemplo, β₀ + β₁x, que está integrado en una función logística (también conocida como función sigmoidea). La fórmula del Clasificador Binario que tenemos al final es la siguiente:

Dónde:

• P (y_I = 1 | X) es la probabilidad de la i^th Observaciones valor objetivo, y_I perteneciente a la clase 1.
• Β₀ y β₁ son los parámetros que se deben aprender.
• mi representa el número de Euler.

Objetivo principal de la fórmula de regresión logística.

La fórmula de regresión logística tiene como objetivo limitar o restringir la salida lineal y / o sigmoidea entre un valor de 0 y 1. La razón principal es para propósitos de interpretabilidad, es decir, podemos leer el valor como una probabilidad simple; Lo que significa que si el valor es mayor que 0,5, se predeciría la clase uno; de lo contrario, se predice la clase 0.

Fuente: GraphPad

Implementación de Python.

Ahora veremos la implementación del lenguaje de programación Python. Para este ejercicio, usaremos el conjunto de datos de la ionosfera que está disponible para descargar desde el Repositorio de aprendizaje automático de la UCI.

# We begin by importing the necessary packages
# to be used for the Machine Learning problem

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

# We read the data into our system using Pandas'
# 'read_csv' method. This transforms the .csv file
# into a Pandas DataFrame object.

dataframe = pd.read_csv('ionosphere.data', header=None)

# We configure the display settings of the
# Pandas DataFrame.

pd.set_option('display.max_rows', 10000000000)
pd.set_option('display.max_columns', 10000000000)
pd.set_option('display.width', 95)

# We view the shape of the dataframe. Specifically
# the number of rows and columns present.
print('This DataFrame Has %d Rows and %d Columns'%(dataframe.shape))

La salida al código anterior sería la siguiente (la forma del marco de datos):

# We print the first five rows of our dataframe.
print(dataframe.head())

La salida del código anterior se verá de la siguiente manera (la siguiente salida está truncada):

# We isolate the features matrix from the DataFrame.
features_matrix = dataframe.iloc[:, 0:34]

# We isolate the target vector from the DataFrame.
target_vector = dataframe.iloc[:, -1]

# We check the shape of the features matrix, and target vector.
print('The Features Matrix Has %d Rows And %d Column(s)'%(features_matrix.shape))
print('The Target Matrix Has %d Rows And %d Column(s)'%(np.array(target_vector).reshape(-1, 1).shape))

La salida para la forma de nuestra matriz de características y el vector objetivo sería la siguiente:

# We use scikit-learn's StandardScaler in order to
# preprocess the features matrix data. This will
# ensure that all values being inputted are on the same
# scale for the algorithm.

features_matrix_standardized = StandardScaler().fit_transform(features_matrix)

# We create an instance of the LogisticRegression Algorithm
# We utilize the default values for the parameters and
# hyperparameters.

algorithm = LogisticRegression(penalty='l2', dual=False, tol=1e-4,
C=1.0, fit_intercept=True,
intercept_scaling=1, class_weight=None,
random_state=None, solver="lbfgs",
max_iter=100, multi_class="auto",
verbose=0, warm_start=False, n_jobs=None,
l1_ratio=None)

# We utilize the 'fit' method in order to conduct the
# training process on our features matrix and target vector.

Logistic_Regression_Model = algorithm.fit(features_matrix_standardized, target_vector)

# We create an observation with values, in order
# to test the predictive power of our model.

observation = [[1, 0, 0.99539, -0.05889, 0.8524299999999999, 0.02306,
0.8339799999999999, -0.37708, 1.0, 0.0376,
0.8524299999999999, -0.17755, 0.59755, -0.44945, 0.60536,
-0.38223, 0.8435600000000001, -0.38542, 0.58212, -0.32192,
0.56971, -0.29674, 0.36946, -0.47357, 0.56811, -0.51171,
0.41078000000000003, -0.46168000000000003, 0.21266, -0.3409,
0.42267, -0.54487, 0.18641, -0.453]]

# We store the predicted class value in a variable
# called 'predictions'.

predictions = Logistic_Regression_Model.predict(observation)

# We print the model's predicted class for the observation.
print('The Model Predicted The Observation To Belong To Class %s'%(predictions))

La salida al bloque de código anterior debe ser la siguiente:

# We view the specific classes the model was trained to predict.

print('The Algorithm Was Trained To Predict One Of The Two Classes: %s'%(algorithm.classes_))

La salida al bloque de código anterior se verá de la siguiente manera:

print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['b'] Is %s"""%(algorithm.predict_proba(observation)[0][0]))
print()
print("""The Model Says The Probability Of The Observation We Passed Belonging To Class ['g'] Is %s"""%(algorithm.predict_proba(observation)[0][1]))

El resultado esperado sería el siguiente:

Conclusión.

Con esto concluye mi artículo. Ahora entendemos la lógica detrás de este algoritmo de aprendizaje automático supervisado y sabemos cómo implementarlo en un problema de clasificación binaria.

Gracias por tu tiempo.

Relacionado