Big Data

Cadena de Markov | Características y aplicaciones de la cadena de Markov

Este artículo fue publicado como entrada para el Blogatón de ciencia de datos.

Introducción

Las cadenas de Markov son excepcionalmente útiles para modelar un proceso estocástico de espacio discreto en tiempo discreto de varios dominios como finanzas (movimiento del precio de las acciones), algoritmos de PNL (transductores de estado finito, modelo de Markov oculto para etiquetado POS), o incluso en ingeniería física ( Movimiento browniano).

Teniendo en cuenta la inmensa utilidad de este concepto en varios dominios y su importancia fundamental para un número significativo de algoritmos en la ciencia de datos, cubriremos en este artículo los siguientes aspectos de la Cadena de Markov:

Formulación de la cadena de Markov y explicación intuitiva
Aspectos y características de una cadena de Markov
Aplicaciones y casos de uso

Formulación de la cadena de Markov y explicación intuitiva

Para entender qué es una cadena de Markov, primero veamos qué es un proceso estocástico, ya que la cadena de Markov es un tipo especial de proceso estocástico.

Un proceso estocástico se define como una colección de variables aleatorias X = {X_t: t∈T} definido en un espacio de probabilidad común, tomando valores en un conjunto común S (el espacio de estados), e indexado por un conjunto T, a menudo N o [0, ∞) and thought of as time (discrete or continuous respectively) (Oliver, 2009). It means that we have observations at a certain time and the outcome is a random variable. Simply put, a stochastic process is any process that describes the evolution in time of a random phenomenon.

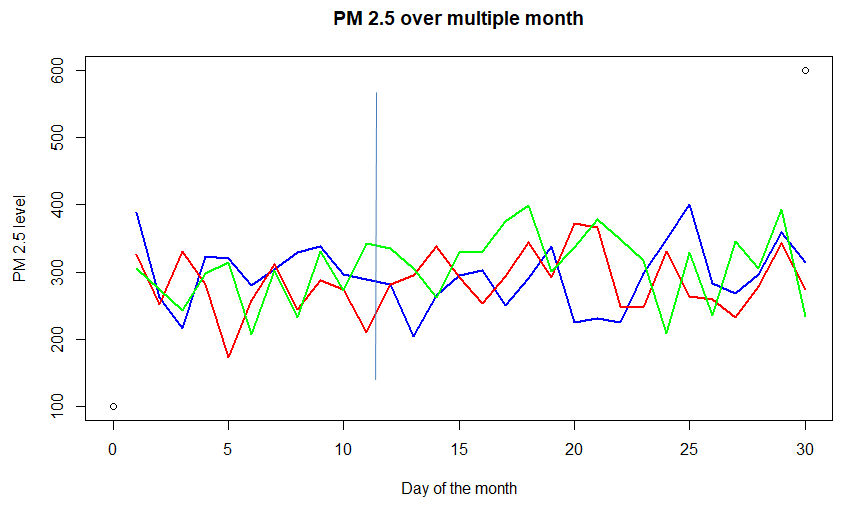
Consider the graph above of concentration of PM (particulate matter) 2.5 in the air over a city for different months. Each of the colored lines -red, blue, and green – (called sample-path) represents a random function of time. Also, consider any day (say 15th of every month), it represents a random variable. Thus it can be considered as a Stochastic process, i.e a process that takes different functional inputs at different times. This particular example is a case for discrete-time (as time is not continuous, observed once a day) with a continuous state (it can take any positive value, not necessarily an integer).

Now that we have a basic intuition of a stochastic process, let’s get down to understand one of the most useful mathematical concepts for Data Science: Markov Chains!

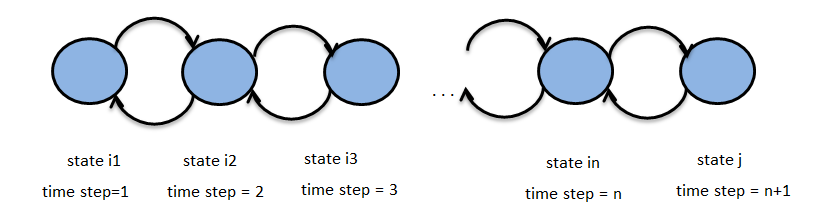
The above figure represents a Markov chain, with states i₁, i₂ ,… , i_n , j for time steps 1, 2, .., n+1. Let {Z_n}_n∈N be the above stochastic process with state space S. N here is the set of integers and represents the time set and Z_n represents the state of the Markov chain at time n. Suppose we have the property :

P(Z_n+1 = j | Z_n = i_n , Z_n-1 = i_n-1 , … , Z₁ = i₁) = P(Z_n+1 = j | Z_n = i_n)

then {Z_n}_n∈N is called a Markov Chain.

This term P(Z_n+1 = j | Z_n= i_n) is called transition probability. Thus we can intuitively see that in order to describe Markov Chain probabilistically, we need (a) the initial state distribution and (b) transition probabilities.

Let’s take the Markov Chain shown below to understand these two terms more formally,

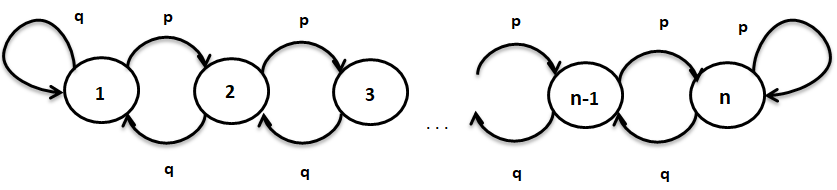
In the Markov chain above, states are 1, 2, …, n and the probability of going from any state k to k+1 (for k =1, 2, …, n-1) is p and going from state k to k-1 is q, where q = 1-p.

The initial state distribution is defined as

π₍₀₎ = [P(X₀=1), P(X₀=2), … , P(X₀ = n)]

La expresión anterior es un vector de fila con elemento que denota la probabilidad de que la cadena de Markov tenga el estado i, donde i = 1, 2,…, n. Todos los elementos de este vector suman 1.

los matriz de probabilidad de transición es como se muestra a continuación :

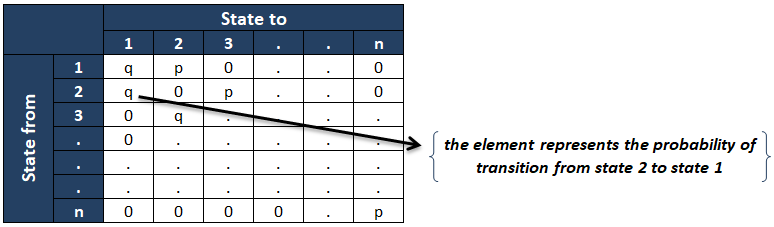
El ij^th elemento de la matriz de probabilidad de transición representa el la probabilidad condicional de la cadena está en el estado j dado que estaba en el estado i en el momento anterior. Si la matriz de probabilidad de transición no depende de «n» (tiempo), entonces la cadena se llama los Cadena de Markov homogénea.

Aspectos y características de una cadena de Markov

En esta sección, veremos los siguientes aspectos principales de una cadena de Markov:

Tiempo del primer golpe: g_l(k)
Tiempo medio de impacto (tiempo de absorción): h_A(k)

El propósito de los dos análisis anteriores es que si tenemos un conjunto de estados deseados (digamos A), y queremos calcular cuánto tiempo tomará alcanzar el estado deseado.

Primera hora de golpe

Imagínese, si queremos conocer la probabilidad (condicional) de que nuestra cadena de Markov, que comienza en algún estado inicial k, alcance el estado l (uno de los muchos estados deseados en A) siempre que alcance cualquier estado en A. ¿Cómo lo haríamos? ¿ese?

Entendamos definiendo algunos términos básicos. Deje T_A ser el tiempo más temprano que se tarda en alcanzar cualquiera de los estados en el conjunto A y k ser algún estado en el espacio de estados pero no en A.

Deje g_l(k) definirse como la probabilidad condicional de alcanzar el estado l en el tiempo T_A a partir del estado k.

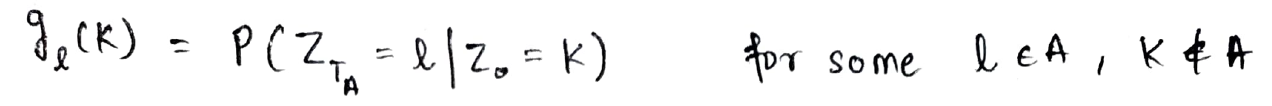
Ahora, usando la propiedad de Markov, consideremos pasar del estado en el tiempo = 0 al estado en el tiempo = T_A como pasar del estado en el tiempo = 0 al estado en el tiempo = 1 y luego pasar del estado en el tiempo = 1 al estado en el tiempo = TA. Lo mismo se representa a continuación:

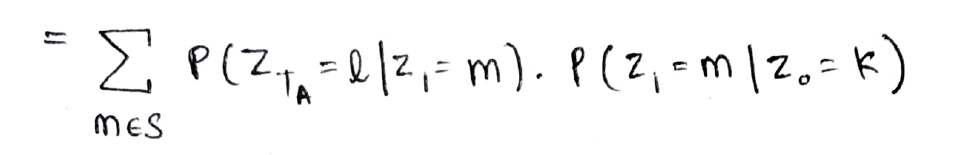
La ecuación anterior se puede interpretar gráficamente así como se muestra a continuación, es decir, en el primer paso puede pasar del estado k a cualquiera de los estados m en un paso y luego ir en T_A-1 paso del estado m al estado deseado l.

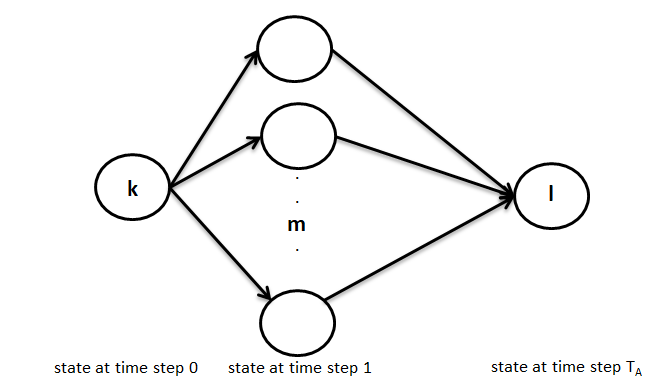
Ahora, el primer término se puede representar como g_l(m) y el segundo término representa la probabilidad de transición del estado k al estado m

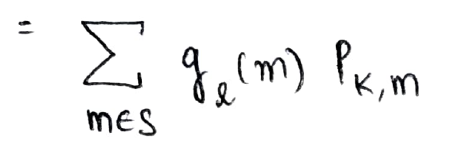
Esta es la forma recursiva en la que calculamos la probabilidad deseada y el enfoque utilizado anteriormente se llama Análisis del primer paso (como lo analizamos en términos del primer paso que toma del estado en el tiempo = 0 al estado en el tiempo = 1)

Tiempo de golpe medio

Usando un enfoque similar al anterior, también podemos calcular el tiempo promedio (esperado) para alcanzar un conjunto deseado de estados (digamos A) a partir de un estado k fuera de A.

Definamos h_A(k) como el tiempo esperado requerido para alcanzar un conjunto A a partir del estado k. Esto se define como se muestra a continuación:

Ahora que sabemos qué es el análisis del primer paso, ¿por qué no utilizarlo de nuevo?

Entonces, ahora escribimos el término de expectativa en términos del primer paso (es decir, alcanzar el estado Z₁) Como se muestra abajo:

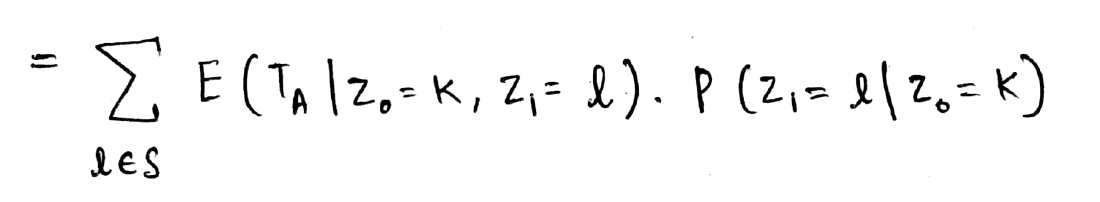
Ahora, usando la propiedad de Markov, podemos eliminar la Z₀ término como conocemos el estado en Z₁. El segundo término en el producto anterior es la probabilidad de transición del estado k al estado l (hemos visto tanto este concepto que ahora se siente como un cálculo 2 + 2 = 4 🙂)

Tenga en cuenta que el término de expectativa a continuación está en términos de Z₁ (y no Z₀) y por lo tanto no podemos escribirlo directamente como h_A(k). Por lo tanto, usamos un truco matemático, sumamos 1 en la expectativa y restamos 1 también para que podamos escribir matemáticamente el estado como Z₀ = l

Y ahora podemos escribirlo como h_A(k).

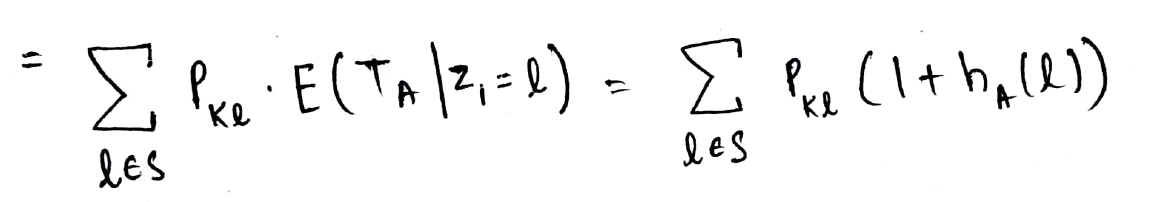
¡Esta es la forma recursiva en la que calculamos la Expectativa deseada!

Ahora conocemos el enfoque fundamental para derivar cualquier propiedad de Markov con las dos nuevas herramientas que poseemos: Comprensión de matriz de probabilidad de transición y Enfoque del análisis del primer paso.

Aplicaciones y casos de uso

Dado que ahora nos sentimos cómodos con el concepto y los aspectos de una cadena de Markov, exploremos y entendamos intuitivamente la siguiente aplicación y casos de uso de las cadenas de Markov.

PNL: modelo de Markov oculto para etiquetado de puntos de venta
Caminata aleatoria como una cadena de Markov

PNL: modelo de Markov oculto para etiquetado de puntos de venta

El etiquetado de parte del habla (POS) es una aplicación importante de PNL. El objetivo en estos problemas es etiquetar cada palabra en una oración dada con un POS apropiado (sustantivo, verbo, adverbio, etc.). En el modelo, tenemos probabilidades de transición de etiquetas, es decir, dado que la etiqueta de la palabra anterior se dice t_i-1, La t_I será la etiqueta de la palabra actual. Y el segundo concepto del modelo es la probabilidad de que dada la etiqueta de la palabra actual sea t_I, la palabra será w_I. Para decirlo más claramente: el modelo de Markov oculto es un tipo de Modelos generativos (conjuntos) en el que los estados ocultos (aquí etiquetas POS) se consideran dados y los datos observados se consideran generados.

La t_I en la figura siguiente se refiere a las etiquetas POS del estado yw_I se refiere a las palabras emitidas por los estados.

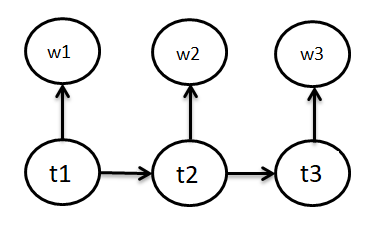
Ahora, veamos el elemento del modelo minuciosamente para ver el proceso de Markov en él aún más claramente. Los elementos del modelo oculto de Markov son:

Un conjunto de estados: aquí Etiquetas POS
La salida de cada estado: aquí ‘palabra’
Estado inicial: aquí comienzo de la oración
Probabilidad de transición de estado: aquí P (t_norte | t_n-1)

Además de ser muy útiles en este aspecto de la PNL, los transductores de estado finito y muchos otros algoritmos se basan en cadenas de Markov.

Caminata aleatoria

Otro fenómeno interesante es el de Random walk, que de nuevo es una Cadena de Markov.

Consideremos la caminata aleatoria, como se muestra arriba, es decir, el movimiento de un paso hacia adelante desde cualquier estado puede ocurrir con una probabilidad py el movimiento hacia atrás de un paso puede ocurrir con una probabilidad q. Aquí el movimiento hacia adelante del estado k al k + 1 depende solo del estado k y, por lo tanto, Random Walk es una cadena de Markov.

Ahora, demos un paso adelante y entendamos el paseo aleatorio como una cadena de Markov usando simulación. Aquí consideramos el caso de la caminata unidimensional, donde la persona puede dar pasos hacia adelante o hacia atrás de cualquier tamaño (tamaño> = 1) con igual probabilidad.

Aquí, he trazado 30 caminatas al azar para desarrollar la intuición en torno al fenómeno. Aquí, el estado inicial de la cadena de Markov es 0 (cero pasos acumulativos inicialmente). Las cosas a tener en cuenta son:

El espacio de estado y el tiempo establecido son ambos discretos (enteros)
Es visualmente claro que en cualquier paso de tiempo dado, el siguiente estado está determinado solo por el estado actual y los pasos de tiempo detrás del paso de tiempo actual no ayudan a predecir dónde estará el estado de la cadena en el próximo paso de tiempo.
Dado que la probabilidad de movimiento hacia adelante es la misma que la del movimiento hacia atrás, el valor esperado del número acumulado de pasos es 0.

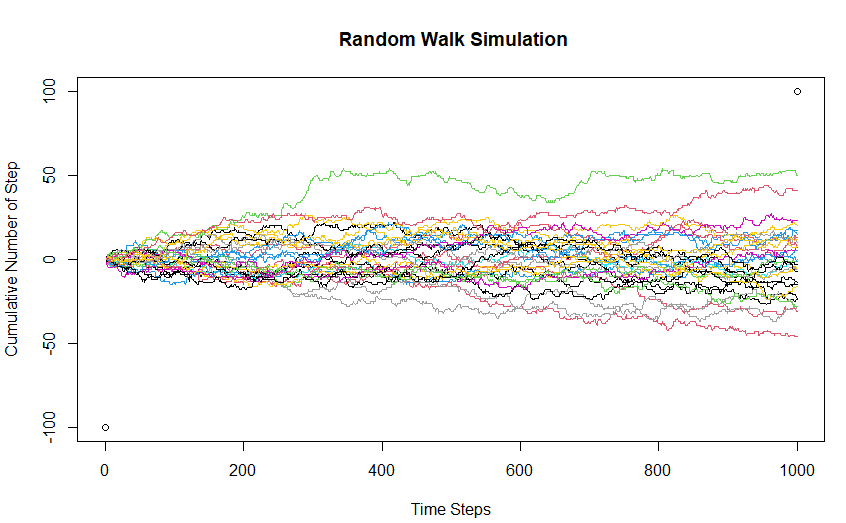
El código para simular un paseo aleatorio básico en R se da a continuación:

plot(c(0,1000),c(-100,100), xlab = "Time Steps", ylab = "Cumulative Number of Step" , main = " Random Walk Simulation")
for (i in 1:30) {
  x <- as.integer(rnorm(1000))
  lines(cumsum(x), type = "l", col=sample(1:10,1)) 
}

La cadena de Markov es una técnica muy poderosa y efectiva para modelar un proceso estocástico de tiempo y espacio discreto. La comprensión de las dos aplicaciones anteriores junto con el concepto matemático explicado se puede aprovechar para comprender cualquier tipo de proceso de Markov.

Nota sobre el autor: Soy estudiante de PGDBA (Diploma de posgrado en análisis de negocios) en IIM Calcutta, IIT Kharagpur e ISI Kolkata, y he completado mi B.TECH de IIT DELHI y tengo una experiencia laboral de ~ 3,5 años en análisis avanzado.

No dude en comunicarse con cualquier discusión sobre el tema en Parth Tyagi | LinkedIn o escríbeme un correo a [email protected]

Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.